Содержание
- 2. Дифференциальные уравнения. Задача о первообразной. Найти функцию такую, что Решение.
- 3. Дифференциальные уравнения. Задача о движении. Материальная точка движется вдоль оси ОХ со скоростью V(t). Найти закон
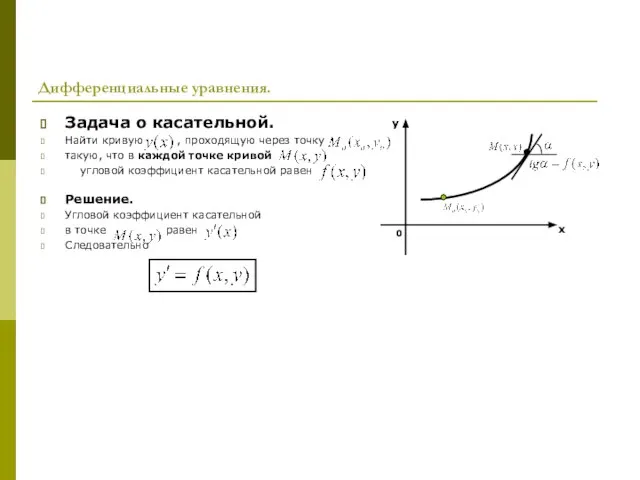
- 4. Дифференциальные уравнения. Задача о касательной. Найти кривую , проходящую через точку такую, что в каждой точке
- 5. Дифференциальные уравнения. Определение 1. Дифференциальным уравнением порядка n называется уравнение вида Определение 2. Порядком дифференциального уравнения
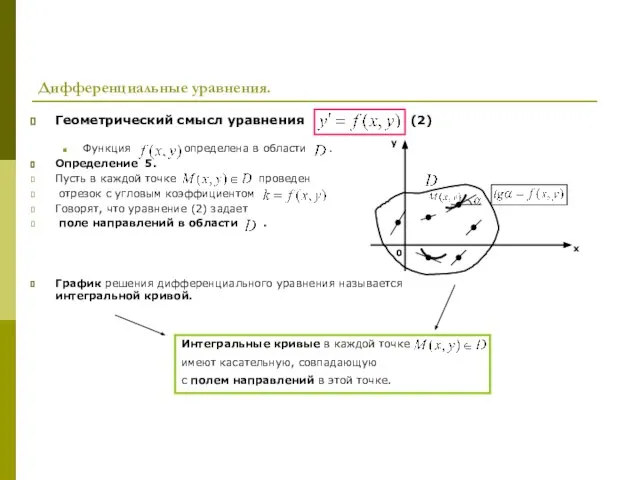
- 6. Дифференциальные уравнения. Геометрический смысл уравнения (2) Функция определена в области . Определение 5. Пусть в каждой
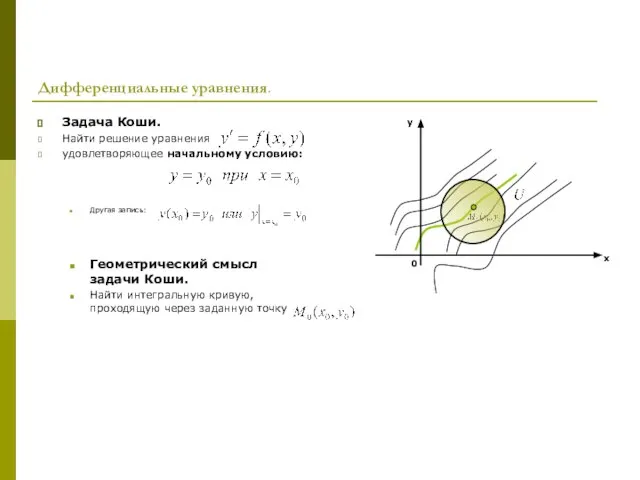
- 7. Дифференциальные уравнения. Задача Коши. Найти решение уравнения удовлетворяющее начальному условию: Другая запись: Геометрический смысл задачи Коши.
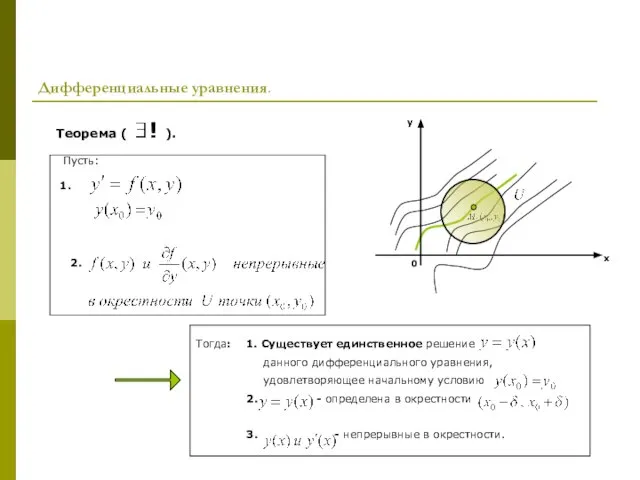
- 8. Дифференциальные уравнения. 0 x y Теорема ( ! ). Пусть: 1. 2. Тогда: 1. Существует единственное
- 9. Дифференциальные уравнения. Пример 2. Найти решение уравнения удовлетворяющее заданному начальному условию: (Решить две задачи Коши). Решение.
- 10. Дифференциальные уравнения. Определение. Общим решением дифференциального уравнения в области называется функция , зависящая от х и
- 11. Дифференциальные уравнения. Пример. Частные решения Д.У.
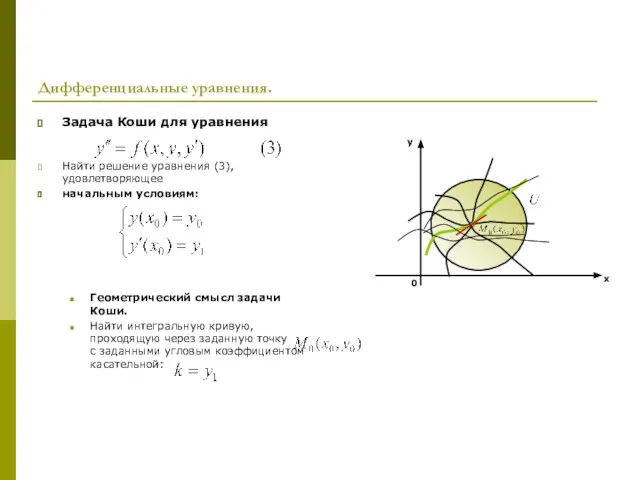
- 12. Дифференциальные уравнения. Задача Коши для уравнения Найти решение уравнения (3), удовлетворяющее начальным условиям: Геометрический смысл задачи
- 13. Дифференциальные уравнения. Теорема ( ! ). Пусть; 1. 2. Тогда: 1. Существует единственное решение данного дифференциального
- 15. Скачать презентацию







 Скалярное прозведение векторов
Скалярное прозведение векторов Решение задач
Решение задач Преобразования графиков функций. 8 класс
Преобразования графиков функций. 8 класс Признаки параллельности прямых. Тест
Признаки параллельности прямых. Тест Лекция_04
Лекция_04 Среднее арифметическое
Среднее арифметическое Квадратичная зависимость
Квадратичная зависимость Логарифмы вокруг нас
Логарифмы вокруг нас Диофантово уравнение
Диофантово уравнение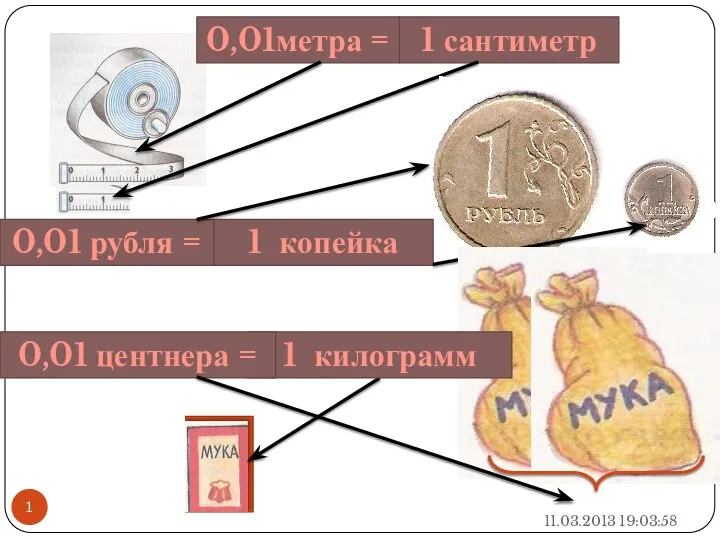 Проценты
Проценты Задачи на построение сечений
Задачи на построение сечений Элективный курс. Алгебра 11 класс. Уроки 07-08
Элективный курс. Алгебра 11 класс. Уроки 07-08 Интегралы. Введение в математический анализ
Интегралы. Введение в математический анализ Связь между суммой и слагаемыми (1 класс)
Связь между суммой и слагаемыми (1 класс) Волшебная страна математики: основы математики для детей 5-6 лет
Волшебная страна математики: основы математики для детей 5-6 лет Названия чисел в записях действий
Названия чисел в записях действий Основные формулы
Основные формулы Задачи на совместную работу
Задачи на совместную работу Проверка деления
Проверка деления Презентация на тему Треугольники. Третий признак равенства
Презентация на тему Треугольники. Третий признак равенства  Математическая статистика 2
Математическая статистика 2 Факториал. Задача со стульями
Факториал. Задача со стульями Геометричне моделювання організаційних кластерних сруктур
Геометричне моделювання організаційних кластерних сруктур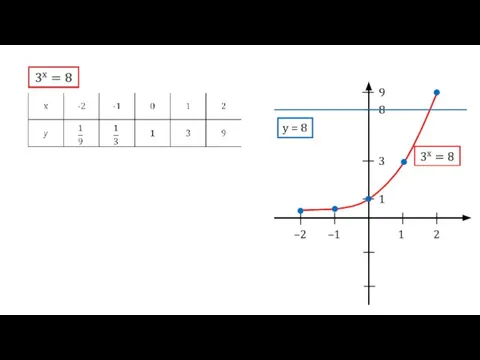 Логарифмы. Возведение в степень. Логарифмирование
Логарифмы. Возведение в степень. Логарифмирование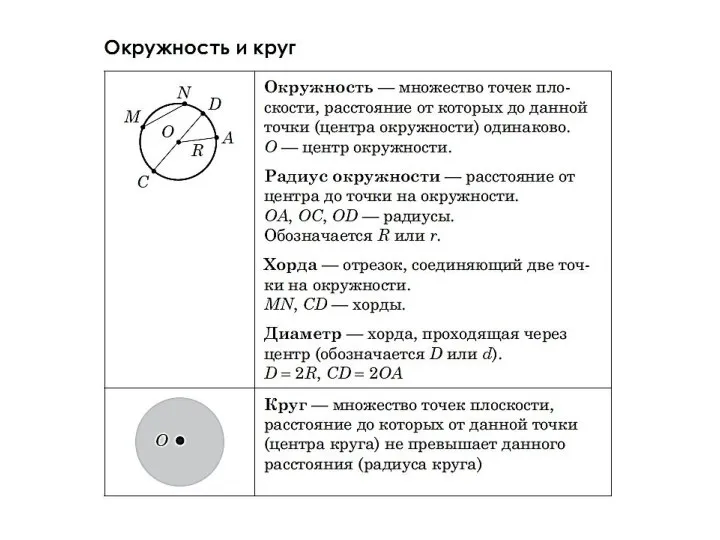 Окружность и круг
Окружность и круг Презентация на тему Решение систем линейных уравнений 7 класс для учителя
Презентация на тему Решение систем линейных уравнений 7 класс для учителя  Метод Крамера
Метод Крамера Презентация на тему Зарождение и история геометрии
Презентация на тему Зарождение и история геометрии