Вписанные и описанные четырехугольники

Определение.
Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника.
В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником.
Вписанные четырёхугольники и их свойства

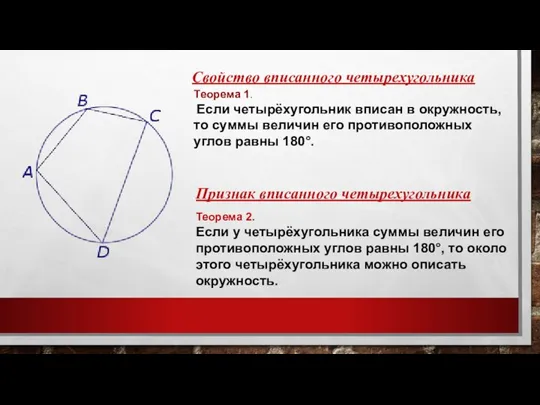
Теорема 1.
Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Свойство вписанного четырехугольника
Признак вписанного четырехугольника
Теорема 2.
Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Окружность, описанная около параллелограмма
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Слайд 6

Дельтоид
Дельтоид – это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.

Произвольный вписанный четырёхугольник
Теорема Птолемея.
Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
AC * BD = AB * CD + BC * AD

Площадь произвольного вписанного четырёхугольника. Формула Брахмагупты
где a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

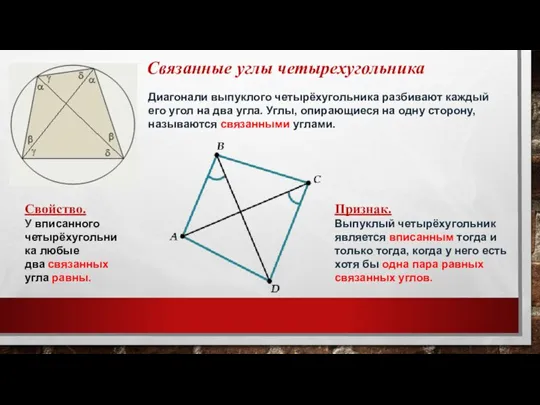
Диагонали выпуклого четырёхугольника разбивают каждый его угол на два угла. Углы, опирающиеся на одну сторону, называются связанными углами.
Свойство.
У вписанного четырёхугольника любые два связанных угла равны.
Признак.
Выпуклый четырёхугольник является вписанным тогда и только тогда, когда у него есть хотя бы одна пара равных связанных углов.
Связанные углы четырехугольника

Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
Радиус окружности, описанной около четырёхугольника

Для радиусов описанной и вписанной окружностей данного четырёхугольника и расстояния между центрами этих окружностей выполняется соотношение:

Описанные четырехугольники
Определение. Окружностью, вписанной в четырёхугольник, называют окружность, которая касается каждой из сторон четырёхугольника
В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником.

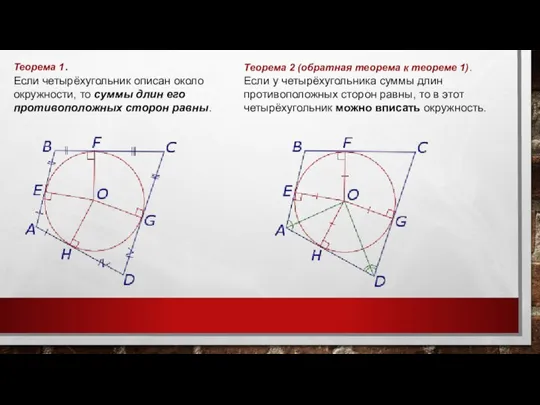
Теорема 1.
Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.
Теорема 2 (обратная теорема к теореме 1).
Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.

Примеры описанных четырёхугольников
Окружность, вписанная в ромб
В любой ромб можно вписать окружность
В любой квадрат можно вписать окружность
Окружность, вписанная в квадрат

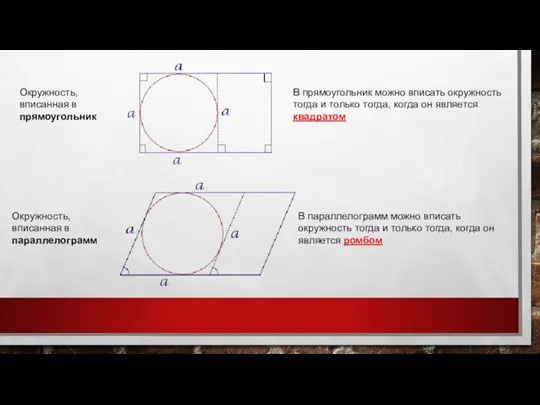
В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом
В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом
Окружность, вписанная в прямоугольник
Окружность, вписанная в параллелограмм

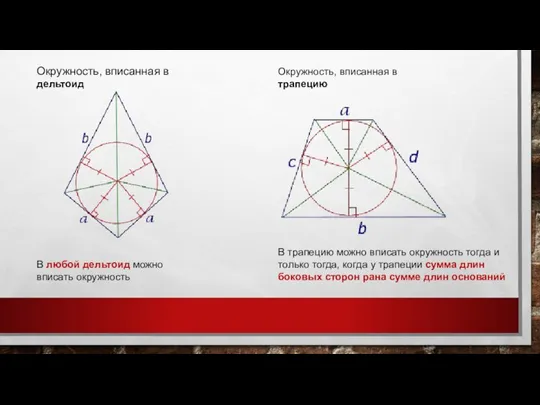
В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований
Окружность, вписанная в трапецию
Окружность, вписанная в дельтоид
В любой дельтоид можно вписать окружность