Содержание
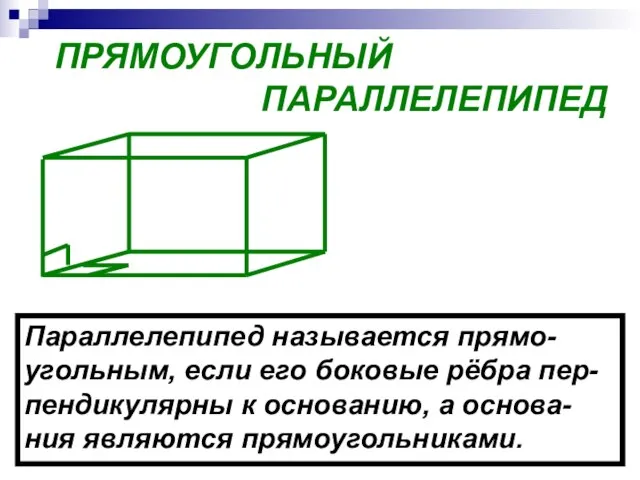
- 2. ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД Параллелепипед называется прямо- угольным, если его боковые рёбра пер- пендикулярны к основанию, а основа-
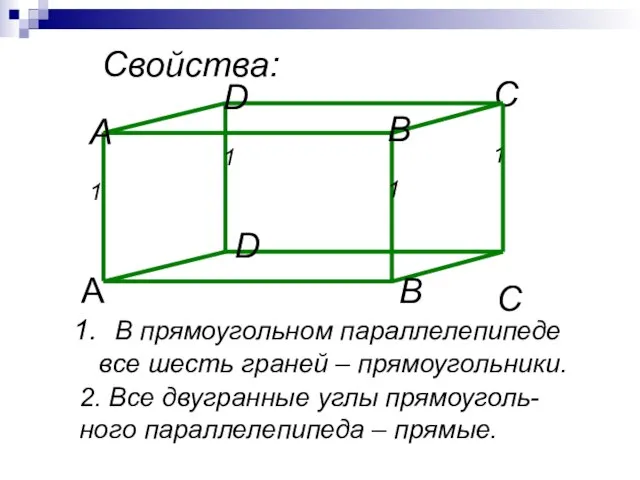
- 3. В прямоугольном параллелепипеде все шесть граней – прямоугольники. 2. Все двугранные углы прямоуголь- ного параллелепипеда –
- 4. Теорема: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений
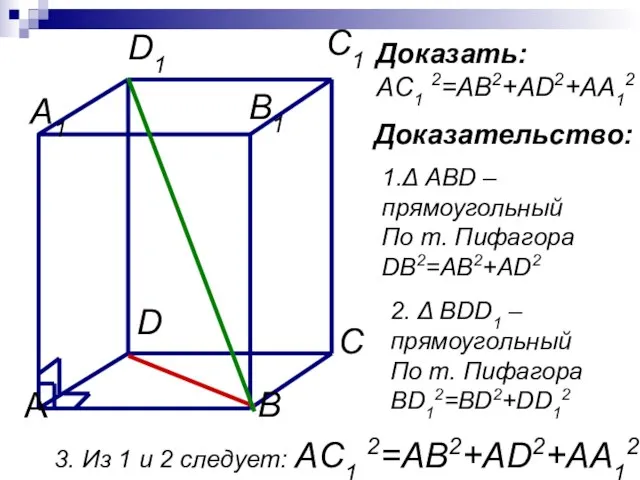
- 5. Доказать: AC1 2=AB2+AD2+AA12 Доказательство: 1.Δ ABD –прямоугольный По т. Пифагора DB2=AB2+AD2 2. Δ BDD1 – прямоугольный
- 6. СЛЕДСТВИЕ: ДИАГОНАЛИ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА РАВНЫ
- 7. b Формулы полной поверхности и объёма прямоугольного параллелепипеда a c d (а=в=с - куб)
- 8. ЗАДАЧИ НА ЕГЭ
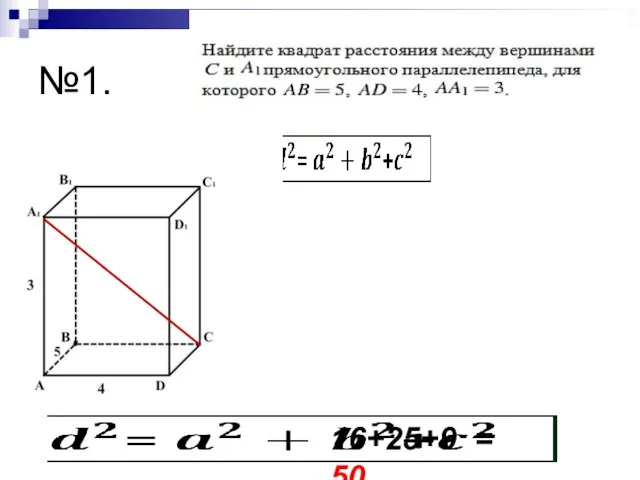
- 9. №1. 16+25+9 = 50.
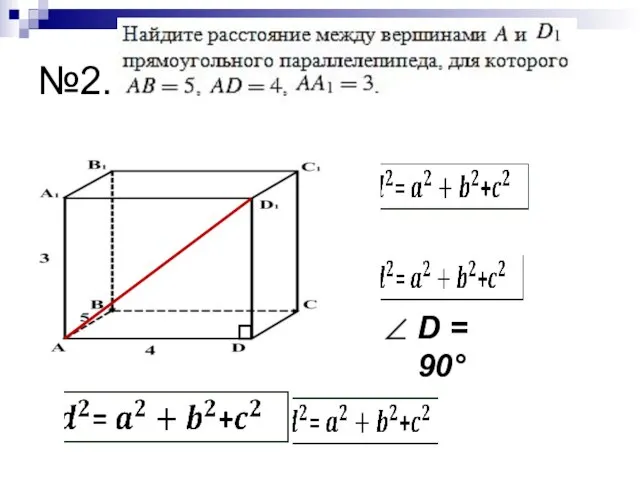
- 10. №2. D = 90°
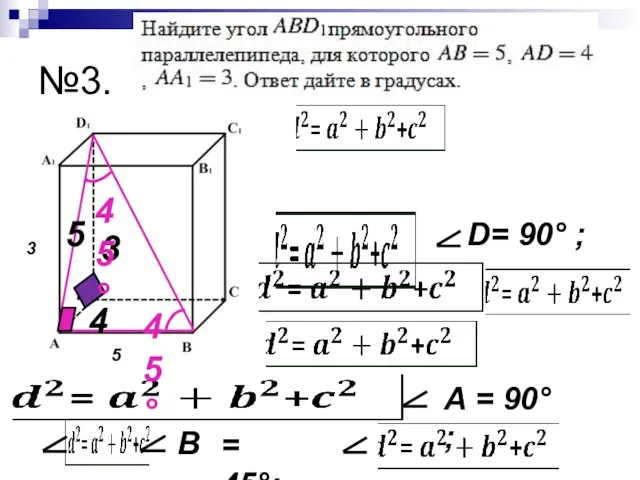
- 11. №3. 3 4 5 D= 90° ; 3 5 B = 45°; 45° 45° A =
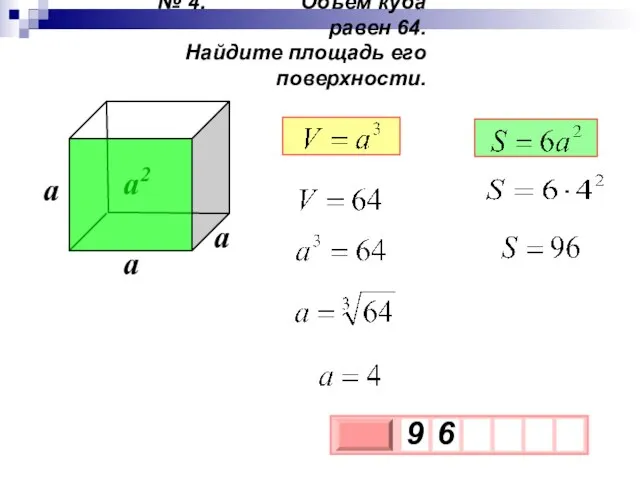
- 12. № 4. Объем куба равен 64. Найдите площадь его поверхности. a2
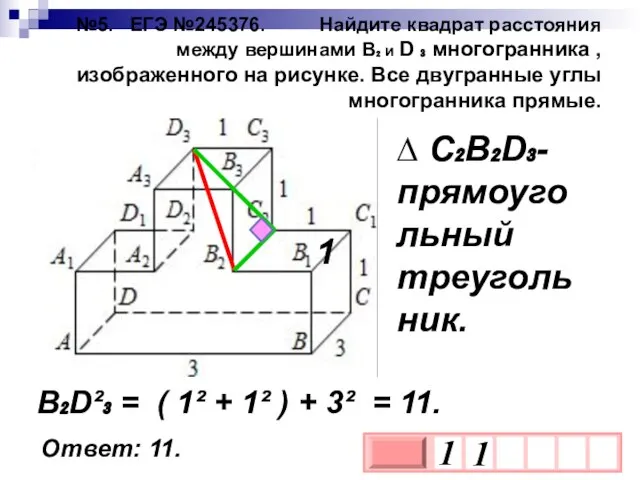
- 13. №5. ЕГЭ №245376. Найдите квадрат расстояния между вершинами B₂ и D ₃ многогранника , изображенного на
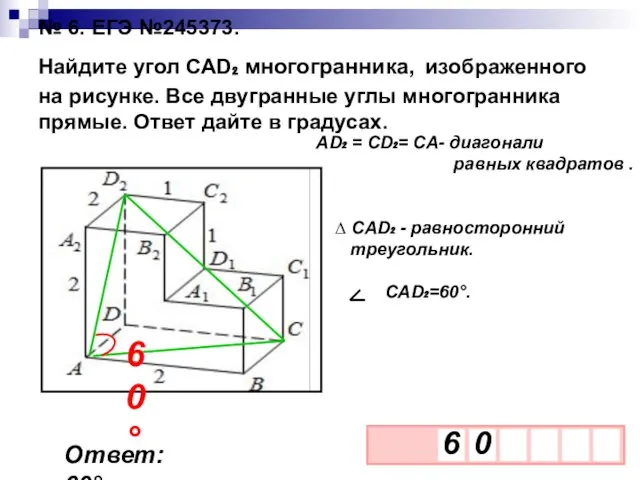
- 14. № 6. ЕГЭ №245373. Найдите угол CAD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
- 15. № 7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). Площадь поверхности данной
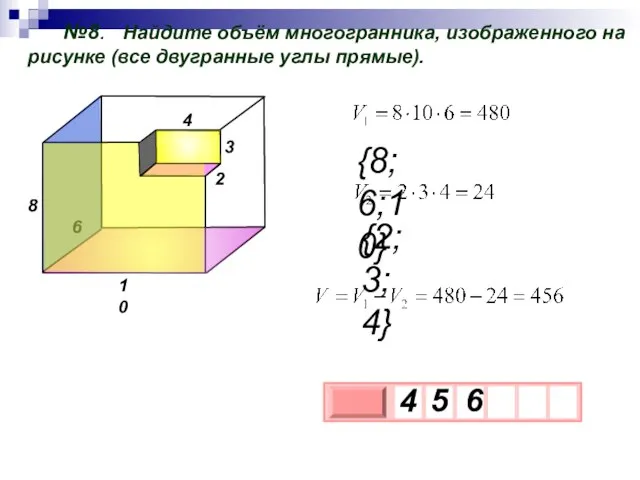
- 16. №8. Найдите объём многогранника, изображенного на рисунке (все двугранные углы прямые). 6 4 3 2 10
- 17. №9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 2 3 4 6
- 18. №10. Найдите объём многогранника, изображенного на рисунке (все двугранные углы прямые). 2 3 4 6 4
- 20. Скачать презентацию







 Лекция 2
Лекция 2 Компланарны ли тройки векторов
Компланарны ли тройки векторов Расстояние от точки до прямой. Решение задач
Расстояние от точки до прямой. Решение задач Простейшие задачи в координатах
Простейшие задачи в координатах Презентация на тему Шар (6 класс)
Презентация на тему Шар (6 класс)  Знаете ли вы... Высота, длина, вес
Знаете ли вы... Высота, длина, вес Фалес Милетский - один из первых геометров
Фалес Милетский - один из первых геометров Задачи математической статистики
Задачи математической статистики Оригами. Проект по математике
Оригами. Проект по математике Вырезаем квадрат
Вырезаем квадрат Измерение массы
Измерение массы Численное интегрирование
Численное интегрирование Математический диктант. Классная работа
Математический диктант. Классная работа Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Проекция группы геометрических тел
Проекция группы геометрических тел Презентация на тему Свойства функций и их графики
Презентация на тему Свойства функций и их графики  Проценты
Проценты Пифагор. Пифагорейская школа
Пифагор. Пифагорейская школа Нулевой угловой коэффицент
Нулевой угловой коэффицент Правильные многогранники
Правильные многогранники Своя игра 2
Своя игра 2 Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств Основное свойство отрезка. Смежные и вертикальные углы
Основное свойство отрезка. Смежные и вертикальные углы Занимательные головоломки
Занимательные головоломки Проценты. Исследовательская работа
Проценты. Исследовательская работа Алгебра и начала математического анализа, 11 класс
Алгебра и начала математического анализа, 11 класс Презентация на тему Площадь круга и кругового сектора
Презентация на тему Площадь круга и кругового сектора  Решение тригонометрических уравнений
Решение тригонометрических уравнений