Содержание
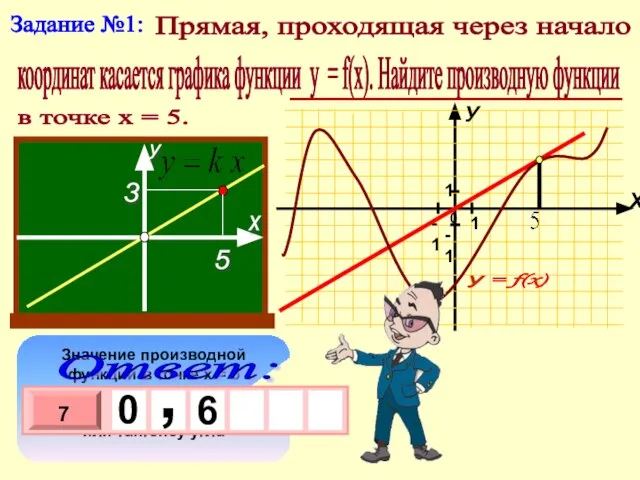
- 3. Прямая, проходящая через начало координат касается графика функции у = f(x). Найдите производную функции в точке
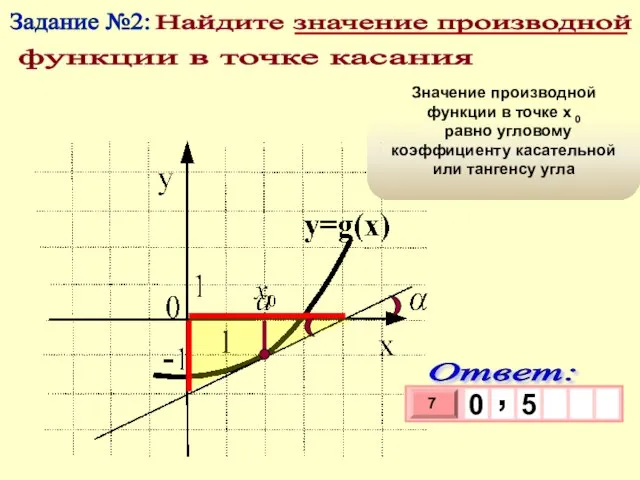
- 4. Задание №2: Найдите значение производной функции в точке касания Значение производной функции в точке х 0
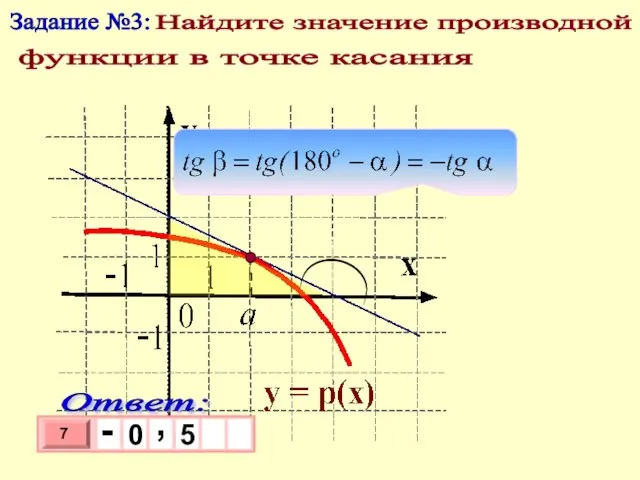
- 5. Задание №3: Найдите значение производной функции в точке касания
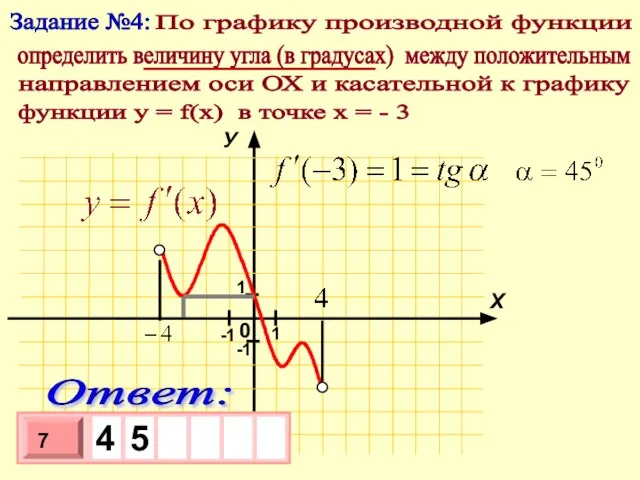
- 6. Задание №4: По графику производной функции определить величину угла (в градусах) между положительным функции у =
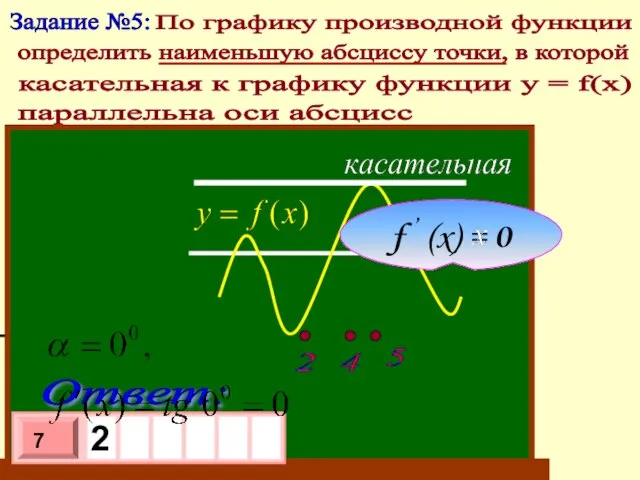
- 7. Задание №5: По графику производной функции определить наименьшую абсциссу точки, в которой параллельна оси абсцисс касательная
- 8. -4 -3 -2 -1 1 2 3 4 5 х y = f /(x) + +
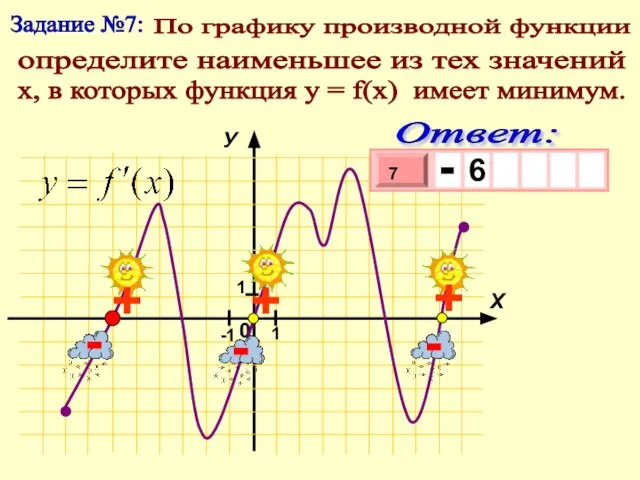
- 9. Задание №7: По графику производной функции определите наименьшее из тех значений х, в которых функция у
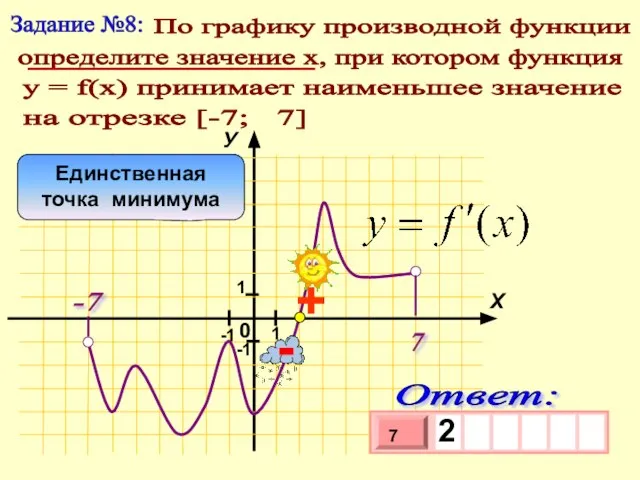
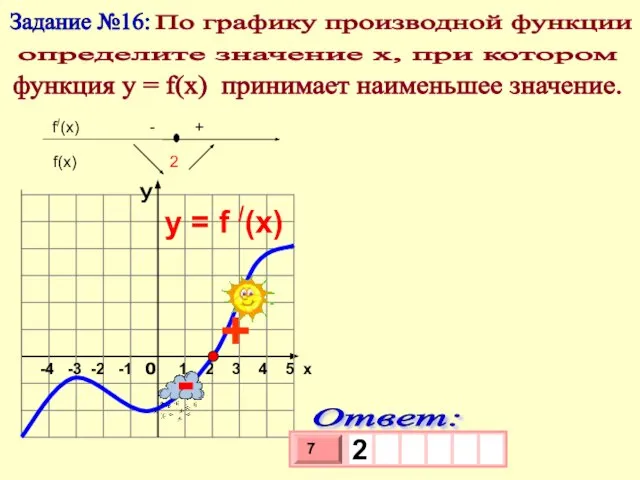
- 10. Задание №8: По графику производной функции определите значение х, при котором функция у = f(x) принимает
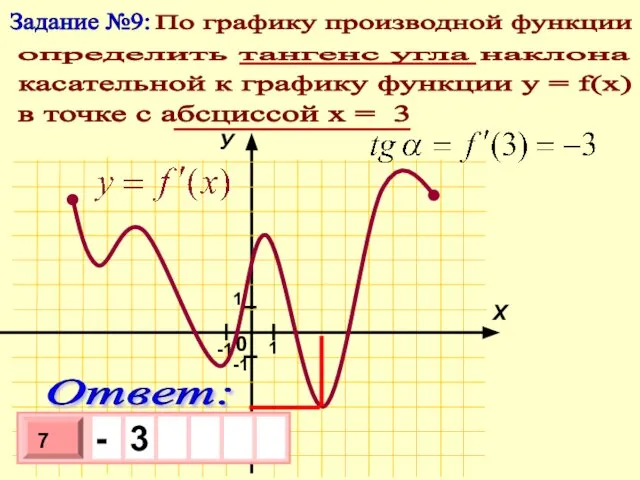
- 11. Задание №9: По графику производной функции определить тангенс угла наклона в точке с абсциссой х =
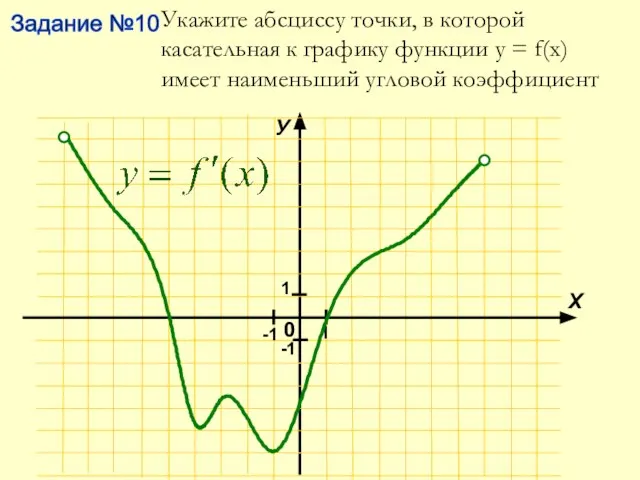
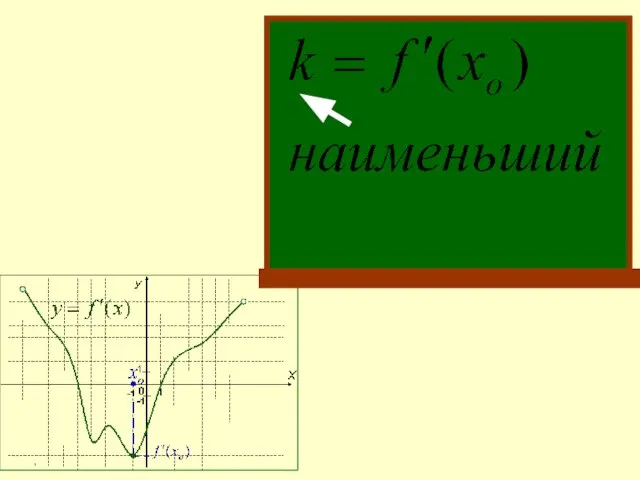
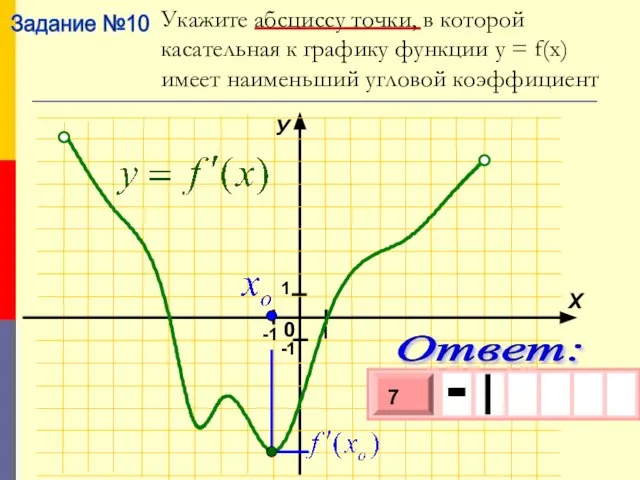
- 12. Задание №10 Укажите абсциссу точки, в которой касательная к графику функции у = f(x) имеет наименьший
- 14. Задание №10 Укажите абсциссу точки, в которой касательная к графику функции у = f(x) имеет наименьший
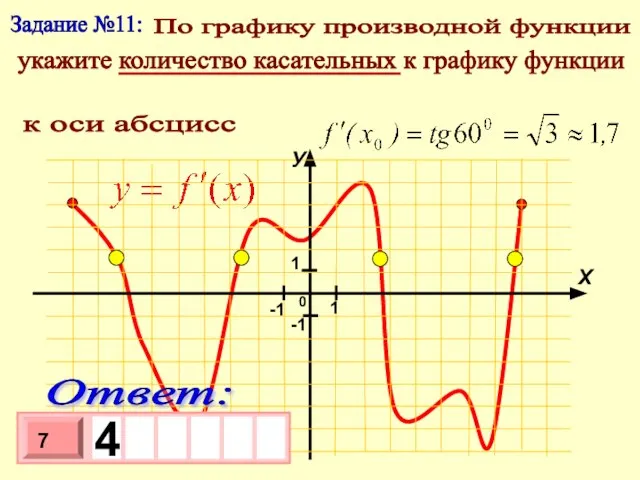
- 15. Задание №11: По графику производной функции укажите количество касательных к графику функции у = f(x), расположенных
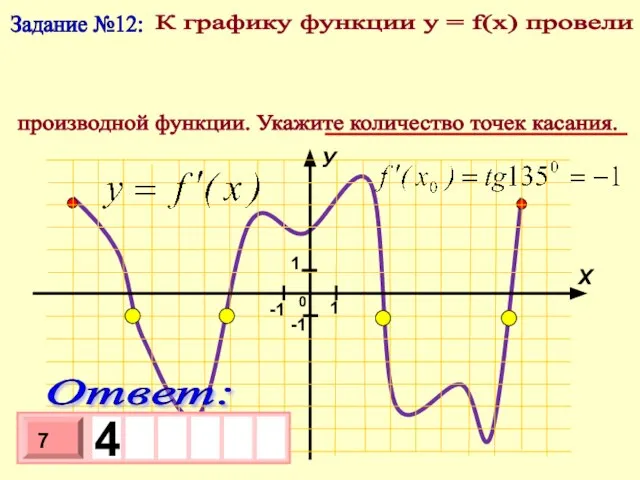
- 16. Задание №12: К графику функции у = f(x) провели касательные под углом 1350 к положительному направлению
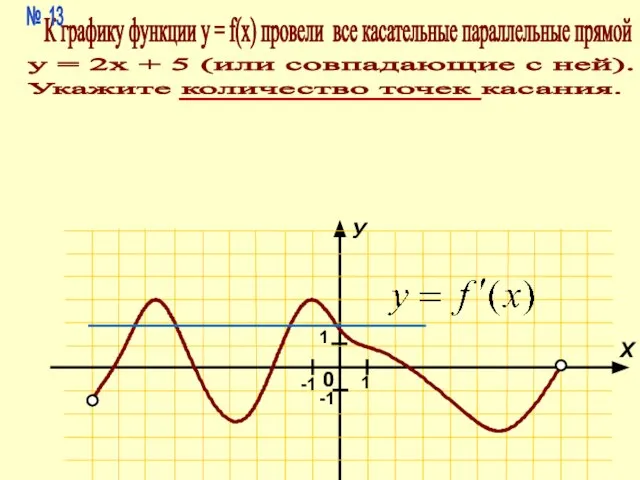
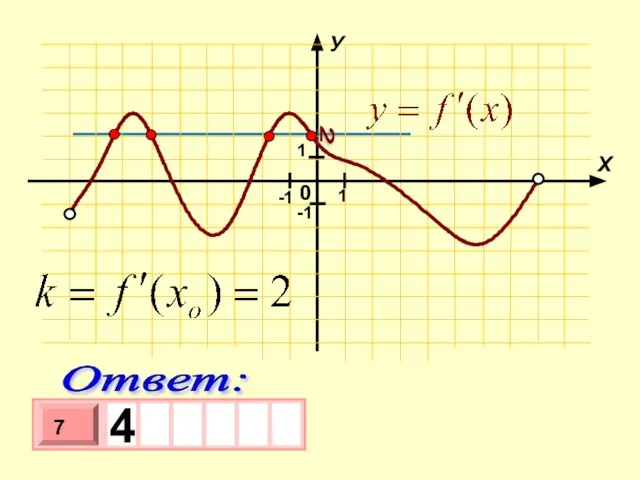
- 17. К графику функции у = f(x) провели все касательные параллельные прямой у = 2х + 5
- 18. 2
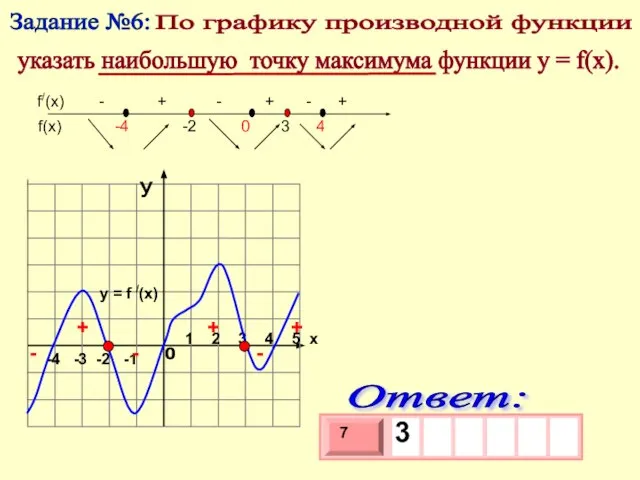
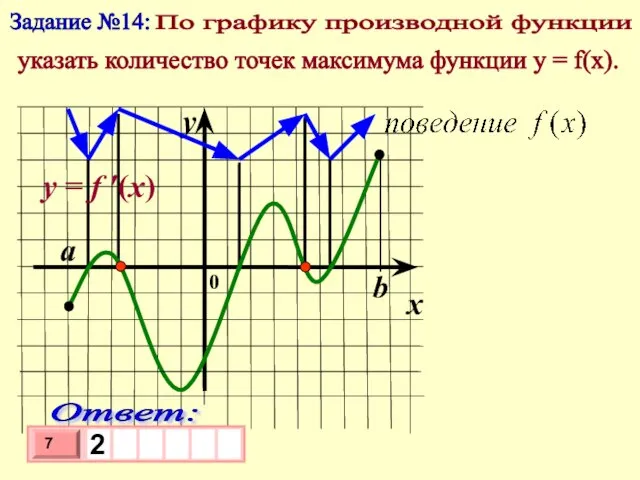
- 19. Задание №14: По графику производной функции указать количество точек максимума функции у = f(x).
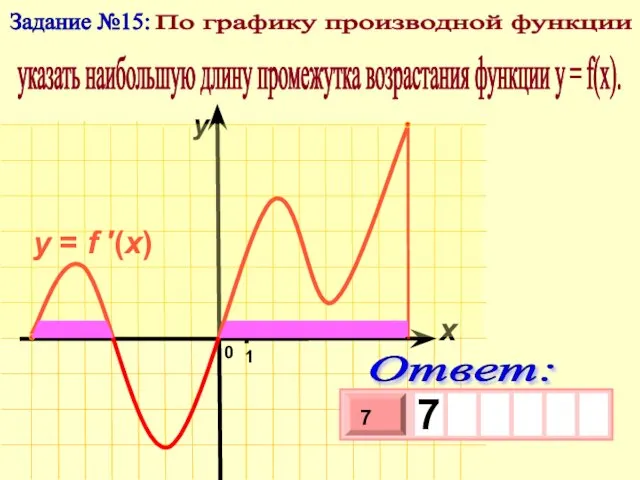
- 20. 1 Задание №15: По графику производной функции указать наибольшую длину промежутка возрастания функции у = f(x).
- 21. -4 -3 -2 -1 1 2 3 4 5 х y = f /(x) У Задание
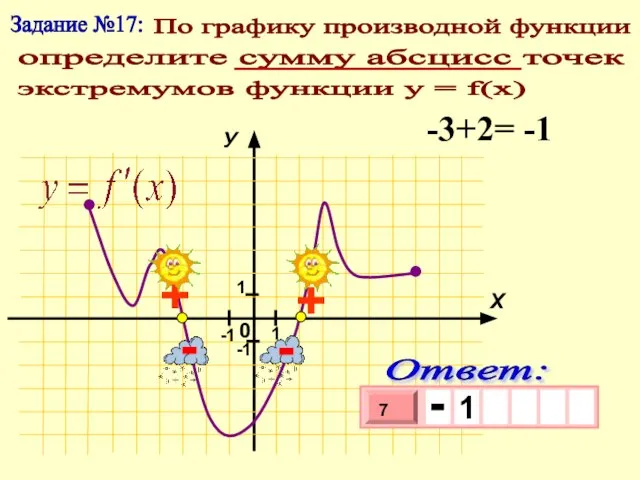
- 22. Задание №17: По графику производной функции определите сумму абсцисс точек экстремумов функции у = f(x) -3+2=
- 24. Скачать презентацию
 Счет и вычисления основа порядка в голове. (Песталоцци)
Счет и вычисления основа порядка в голове. (Песталоцци) История метрологии и теории измерений
История метрологии и теории измерений Решение задач при помощи уравнений
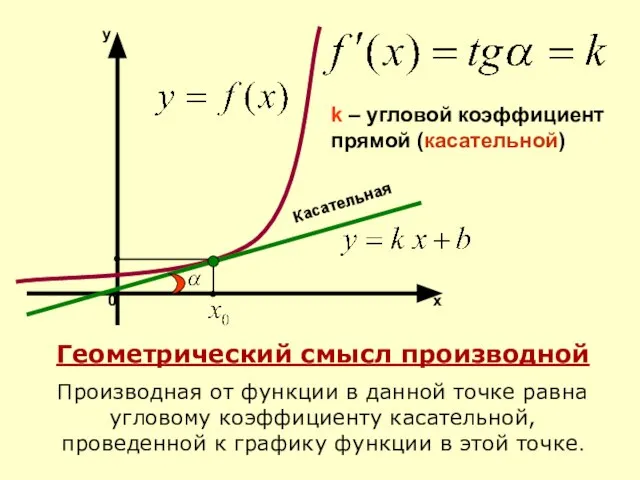
Решение задач при помощи уравнений Производная сложной функции. Исследование функции с помощью производной. Дифференциал
Производная сложной функции. Исследование функции с помощью производной. Дифференциал Умножение одночлена на многочлен
Умножение одночлена на многочлен Канторово множество (канторов дисконтинуум, пыль Кантора)
Канторово множество (канторов дисконтинуум, пыль Кантора) Исчисление высказываний
Исчисление высказываний Презентация на тему Скалярное произведение векторов
Презентация на тему Скалярное произведение векторов  Оформление заданий по математике согласно федеральным образовательным стандартам Программа школа 2100
Оформление заданий по математике согласно федеральным образовательным стандартам Программа школа 2100 Внеклассное мероприятие. Путешествие в мир многогранников
Внеклассное мероприятие. Путешествие в мир многогранников Симметрия. Виды симметрии
Симметрия. Виды симметрии Условная минимизация. Методы модифицированной функции Лагранжа
Условная минимизация. Методы модифицированной функции Лагранжа Принцип Дирихле
Принцип Дирихле Геометрический рисунок. Радиус, центр шара (сферы), диаметр. 6 класс
Геометрический рисунок. Радиус, центр шара (сферы), диаметр. 6 класс Проценты. Ж.Ж. Руссо (1712–1778 гг.)
Проценты. Ж.Ж. Руссо (1712–1778 гг.) Кривая Лоренца. Решение задач
Кривая Лоренца. Решение задач Модуль. Определение. Свойства. Геометрический смысл модуля
Модуль. Определение. Свойства. Геометрический смысл модуля Графики и диаграммы
Графики и диаграммы Дроби. Зажжение олимпийского огня 7 февраля 2014 года, город Сочи
Дроби. Зажжение олимпийского огня 7 февраля 2014 года, город Сочи Метод неопределенных коэффициентов
Метод неопределенных коэффициентов Частотная таблица
Частотная таблица Презентация на тему ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ
Презентация на тему ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ  Уравнение касательной к графику функции
Уравнение касательной к графику функции Презентация на тему Простейшие задачи в координатах (9 класс)
Презентация на тему Простейшие задачи в координатах (9 класс)  Сложение и вычитание трёхзначных чисел
Сложение и вычитание трёхзначных чисел Тренировка интеллекта. Задачи на логику
Тренировка интеллекта. Задачи на логику Решение задач по теме Теорема Пифагора и площади фигур. 8 класс
Решение задач по теме Теорема Пифагора и площади фигур. 8 класс Игра-тренажер по математике Сложение и вычитание в пределах 20
Игра-тренажер по математике Сложение и вычитание в пределах 20