Содержание
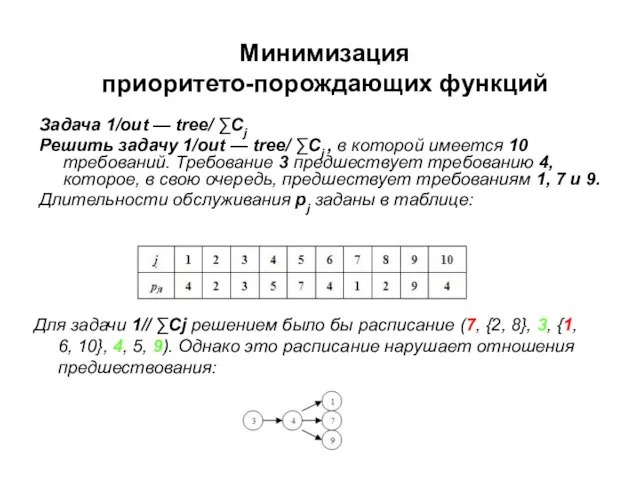
- 2. Минимизация приоритето-порождающих функций Задача 1/out — tree/ ∑Cj Решить задачу 1/out — tree/ ∑Cj , в
- 3. Минимизация приоритето-порождающих функций Обозначим Пr - множество всех перестановок πr = (i1, ... , ir) элементов
- 4. Минимизация приоритето-порождающих функций Функция F(π), определенная на множестве Пn называется приоритето-порождающей (ППФ), если существует функция ω(π),
- 5. Минимизация приоритето-порождающих функций Множество N является частично упорядоченным, если задано отношение предшествования (бинарное, транзитивное, антирефлексивное отношение),
- 6. Минимизация приоритето-порождающих функций Многие задачи построения оптимальных расписаний сводятся к минимизации ППФ на частично упорядоченных множествах
- 7. Примеры приоритето-порождающих функций Можно доказать, что: для задачи 1/prec/ ΣCj целевая функция является ППФ с функцией
- 8. Методы минимизации приоритето-порождающих функций на частично упорядоченных множествах Пусть задано частично упорядоченное множество N с графом
- 9. Методы минимизации приоритето-порождающих функций на частично упорядоченных множествах Введем операции над бесконтурными орграфами, не содержащими транзитивных
- 10. Методы минимизации приоритето-порождающих функций на частично упорядоченных множествах Цепь (i1, ..., ik), где компоненты ij являются
- 11. Алгоритм минимизации ППФ на частично упорядоченных множествах Задача 1/out — tree/ F , где F –
- 12. Алгоритм минимизации ППФ на частично упорядоченных множествах (продолжение) Построим цепь (i0, i1, ..., iν). Если ω(i0)
- 13. Алгоритм минимизации ППФ на частично упорядоченных множествах (продолжение) 3. Повторяем описанный процесс до тех пор, пока
- 14. Алгоритм минимизации ППФ на частично упорядоченных множествах (продолжение) В случае, когда граф G – входящее дерево,
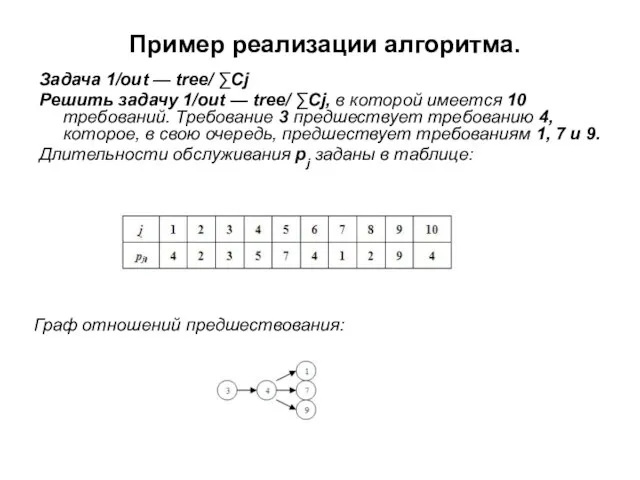
- 15. Пример реализации алгоритма. Задача 1/out — tree/ ∑Cj Решить задачу 1/out — tree/ ∑Cj, в которой
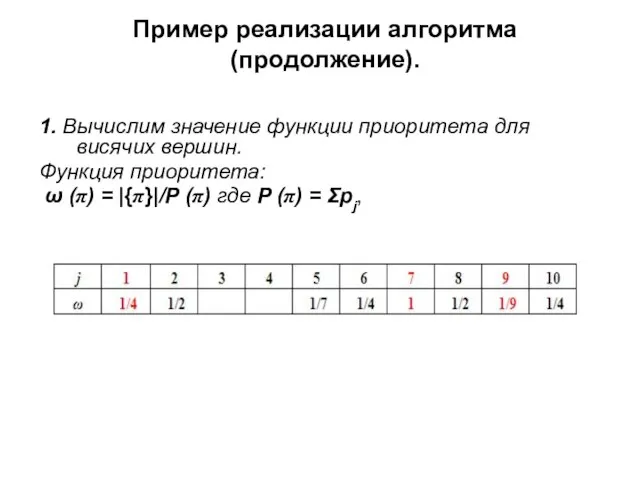
- 16. Пример реализации алгоритма (продолжение). 1. Вычислим значение функции приоритета для висячих вершин. Функция приоритета: ω (π)
- 17. Пример реализации алгоритма (продолжение). 2а. Опорной вершиной является вершина 4, все прямые потомки которой 1, 7
- 18. Пример реализации алгоритма (продолжение). 2б. Цепь (4, 7, 1, 9) не является ω-цепью, поскольку значения функции
- 19. Пример реализации алгоритма (продолжение). 3а. Опорной вершиной является вершина 3, ω-цепь для потомков вершины 3: ([4,
- 20. Пример реализации алгоритма (продолжение). 3б. Цепь (3, [4, 7], 1, 9) не является ω-цепью поскольку значения
- 22. Скачать презентацию















![Пример реализации алгоритма (продолжение). 3б. Цепь (3, [4, 7], 1, 9) не](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/836573/slide-19.jpg)
 Определение знаков коэффициентов K и b в линейной функции по их графикам
Определение знаков коэффициентов K и b в линейной функции по их графикам Графы
Графы Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ
Презентация на тему ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ  Векторная алгебра
Векторная алгебра Презентация на тему Геометрическая прогрессия и ее свойство
Презентация на тему Геометрическая прогрессия и ее свойство  Логарифм
Логарифм Аттестационная работа. Решение сложных задач по математике
Аттестационная работа. Решение сложных задач по математике Головоломки и занимательные задачи
Головоломки и занимательные задачи 1_1_matritsy (1)
1_1_matritsy (1) Иллюстрации географических объектов на Луне
Иллюстрации географических объектов на Луне Подобие треугольников. Первый признак подобия
Подобие треугольников. Первый признак подобия Презентация на тему Призма и ее свойства
Презентация на тему Призма и ее свойства  Кратные интегралы
Кратные интегралы Параллельные прямые. Практическая работа
Параллельные прямые. Практическая работа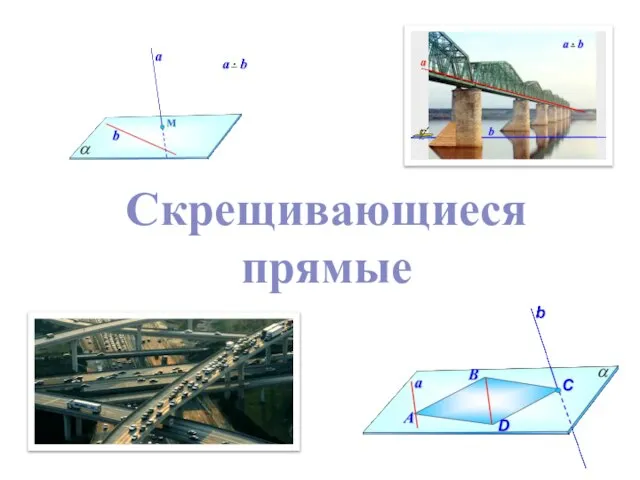 Скрещивающиеся прямые
Скрещивающиеся прямые Плоские деревья и числа Каталана
Плоские деревья и числа Каталана Упрощение логических операций
Упрощение логических операций Прямоугольные треугольники
Прямоугольные треугольники Презентация на тему Проценты
Презентация на тему Проценты  Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Математический анализ. Лекция 1
Математический анализ. Лекция 1 Движение. Поворот
Движение. Поворот Случаи вычитания 11-
Случаи вычитания 11- Слагаемое. Сумма. 1 класс
Слагаемое. Сумма. 1 класс Блез Паскаль
Блез Паскаль Знаки препинания в сложном предложении
Знаки препинания в сложном предложении Выполни вычисления
Выполни вычисления Индивидуальные задания. Урок 15
Индивидуальные задания. Урок 15