Вычисление пределов. Раскрытие неопределенностей

Было домашнее задание на сегодня:
+ знать ответы на следующие вопросы:
С какими математиками связано понятие «Предел»?
Как вычислить предел?
Как раскрыть неопределенность вида 0/0?
Как раскрыть неопределенность вида 0/0, если f(x) – иррациональная дробь?
Уметь формулировать теоремы.

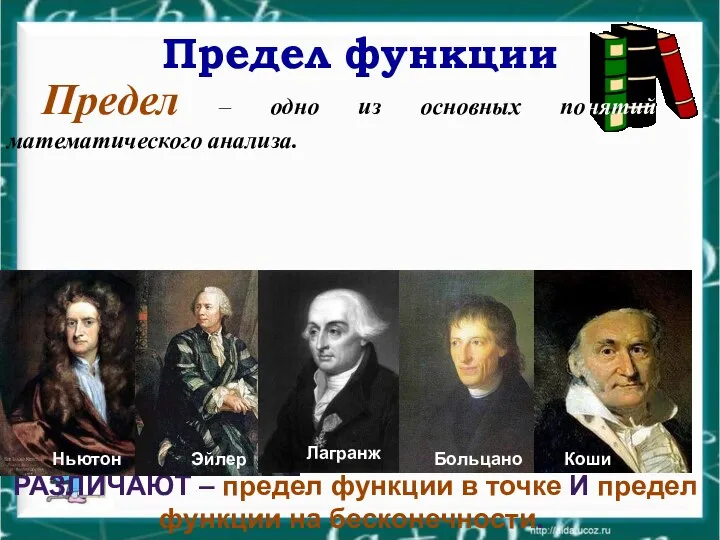
Предел функции
Предел – одно из основных понятий математического анализа.
РАЗЛИЧАЮТ – предел функции в точке И предел функции на бесконечности.
Ньютон
Эйлер
Лагранж
Больцано
Коши

Было домашнее задание на сегодня:
+ знать ответы на следующие вопросы:
С какими математиками связано понятие «Предел»?
Как вычислить предел?
Как раскрыть неопределенность вида 0/0?
Как раскрыть неопределенность вида 0/0, если f(x) – иррациональная дробь?
Уметь формулировать теоремы.

ТЕОРЕМА 1.
Предел СУММЫ (разности) 2-х функций равен СУММЕ (разности) их пределов, если последние существуют:

ТЕОРЕМА 2.
Предел константы равен самой этой константе.

ТЕОРЕМА 3.
Предел ПРОИЗВЕДЕНИЯ 2-х функций равен ПРОИЗВЕДЕНИЮ их пределов, если последние существуют:

ТЕОРЕМА 4.
Предел ОТНОШЕНИЯ 2-х функций равен ОТНОШЕНИЮ их пределов, если последние существуют и ПРЕДЕЛ ЗНАМЕНАТЕЛЯ ОТЛИЧЕН ОТ 0:

ТЕОРЕМА 5.
Постоянный множитель можно выносить за знак предела

ТЕОРЕМА 6.
Предел СТЕПЕНИ переменного равен той же степени предела основания:

Упражнения (13 примеров):

Упражнения (13 примеров):

06.09.2016