Содержание
- 2. Содержание. Построение графиков функций y=af(x) Построение графиков функций y=af(x)+n Построение графиков функций y=af(x-m) Построение графиков функций
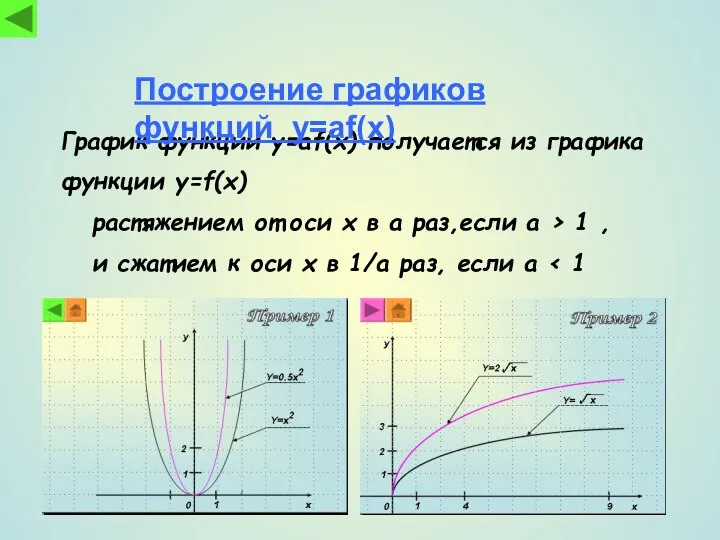
- 3. График функции y=af(x) получается из графика функции y=f(x) растяжением от оси x в a раз,если a
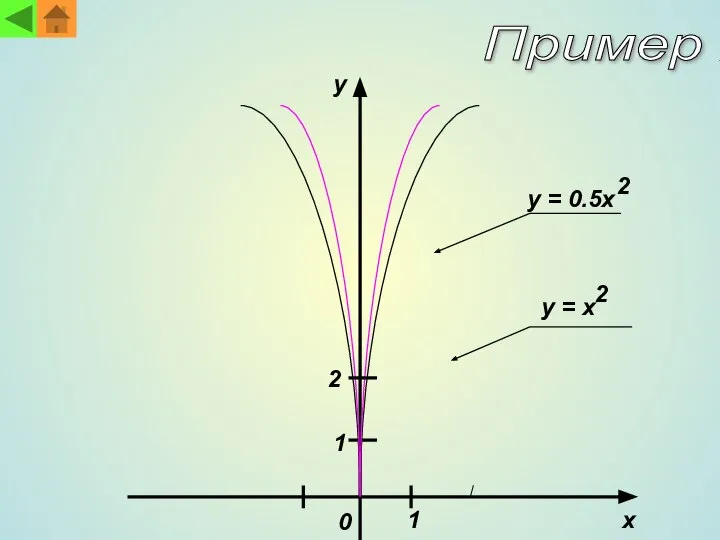
- 4. x 0 y y = 0.5x y = x 2 2 1 1 2 Пример 1
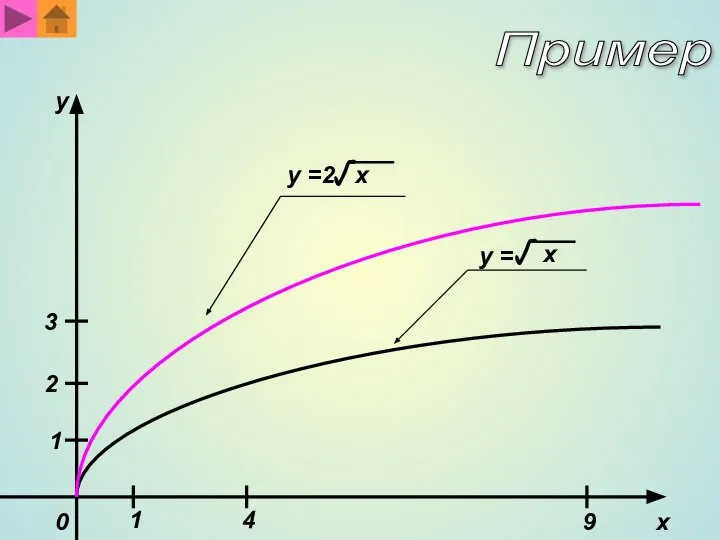
- 5. 1 4 9 y x 0 1 2 3 y =2 √ x y = √
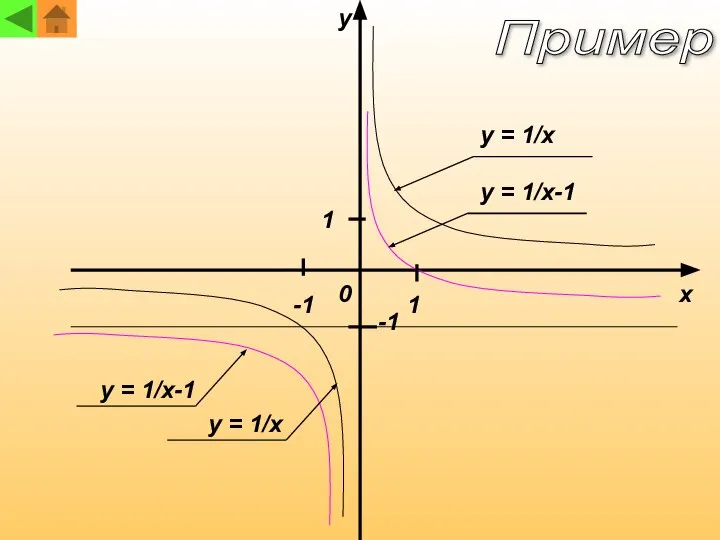
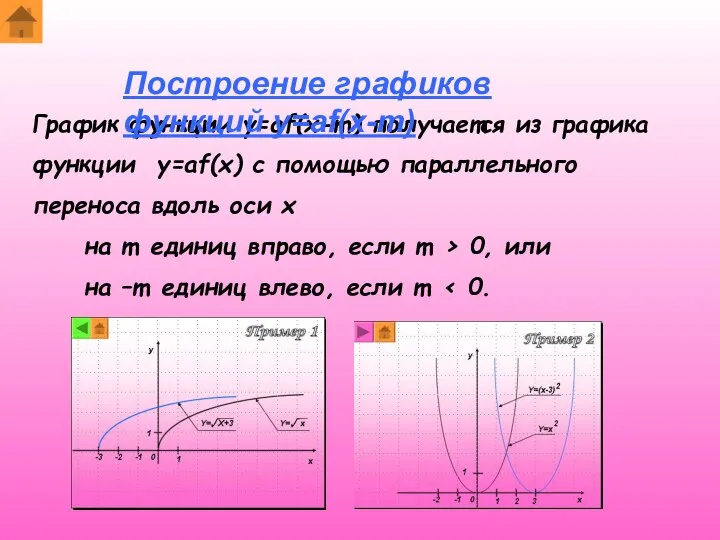
- 6. График функции y=af(x)+n получается из графика функции y=af(x) с помощью параллельного переноса вдоль оси y на
- 7. x y 1 -1 1 0 y = 1/x y = 1/x-1 y = 1/x y
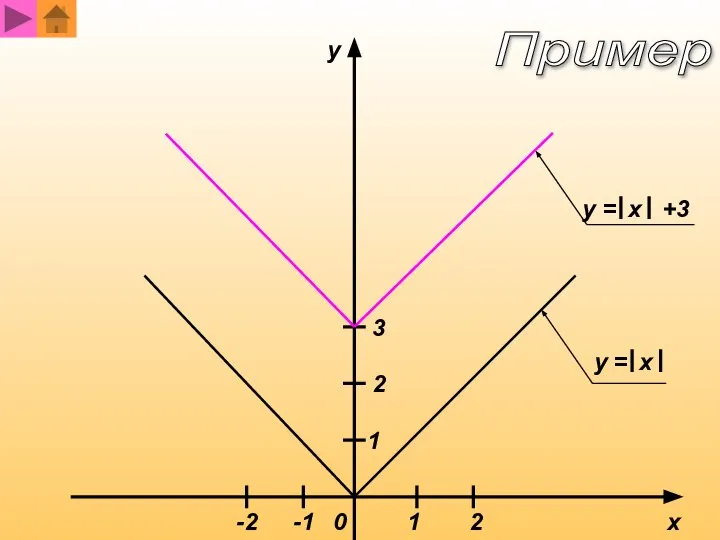
- 8. y x 0 1 1 -1 2 2 -2 y = y = x x +3
- 9. График функции y=af(x-m) получается из графика функции y=af(x) с помощью параллельного переноса вдоль оси x на
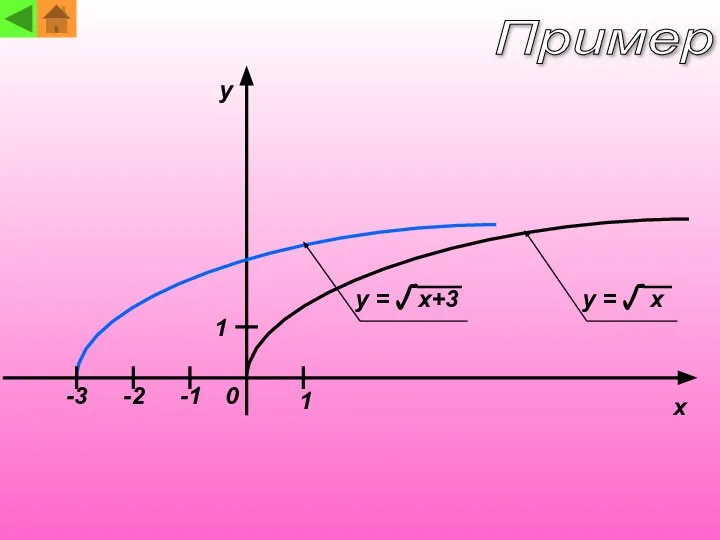
- 10. y x 0 1 1 -1 -2 -3 y = y = √ √ x+3 x
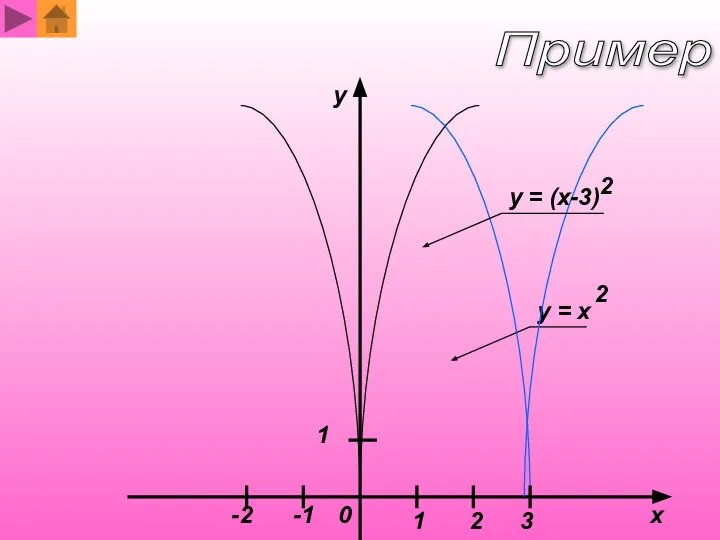
- 11. y = x 2 y = (x-3) 2 x y 1 1 -1 0 2 -2
- 12. График функции y=af(x-m)+n получается из графика с помощью двух параллельных переносов : сдвига вдоль оси x
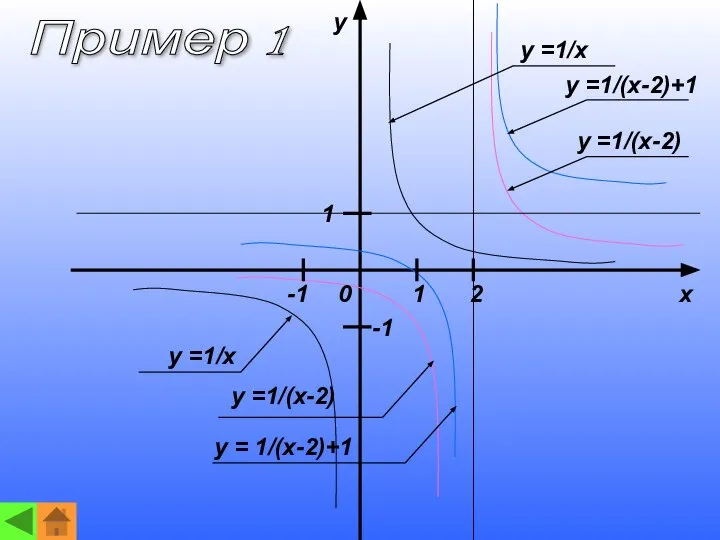
- 13. y x 1 2 1 -1 0 y =1/x y =1/x y =1/(x-2)+1 y =1/(x-2) y
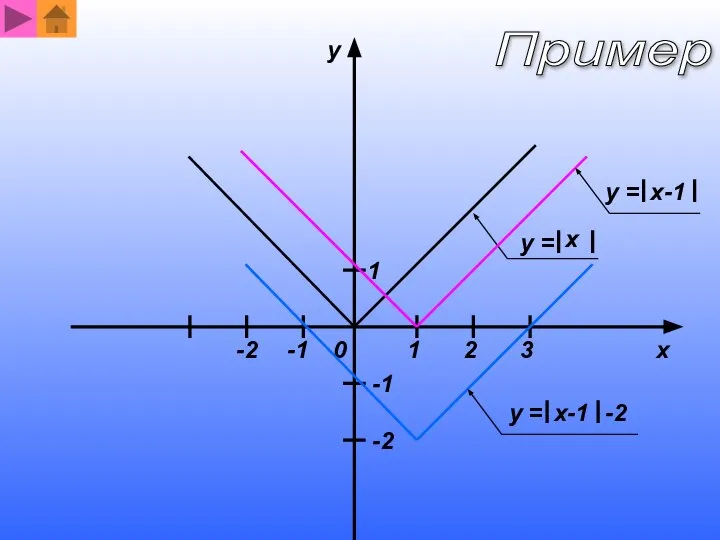
- 14. y = x x-1 1 1 2 3 -1 -1 -2 -2 y 0 y =
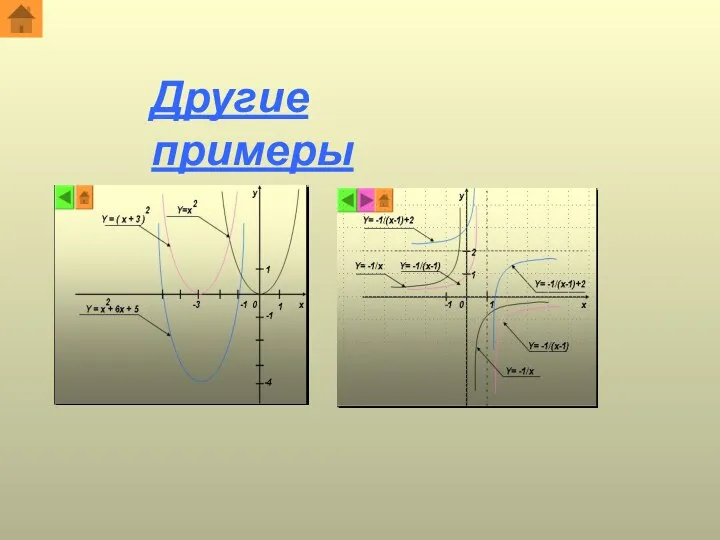
- 15. Другие примеры
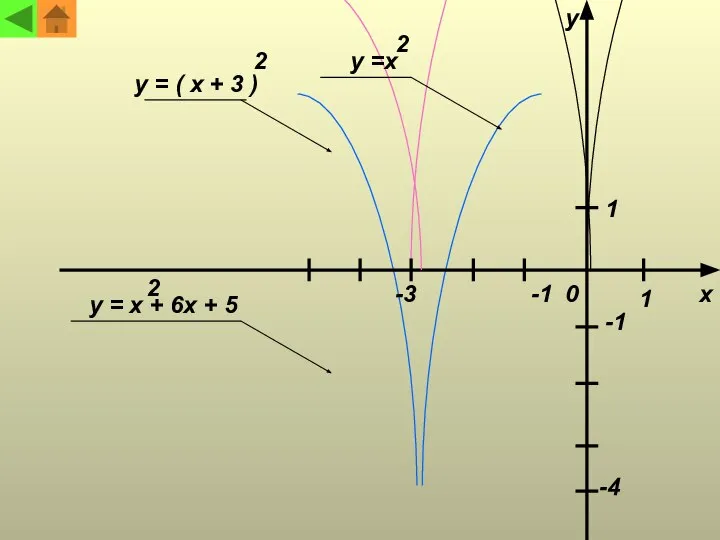
- 16. Построить график функции y = x + 6x + 5 2 Решение. Преобразуем трехчлен, выделив в
- 17. y x 0 1 1 -1 -1 -3 -4 y =x y = ( x +
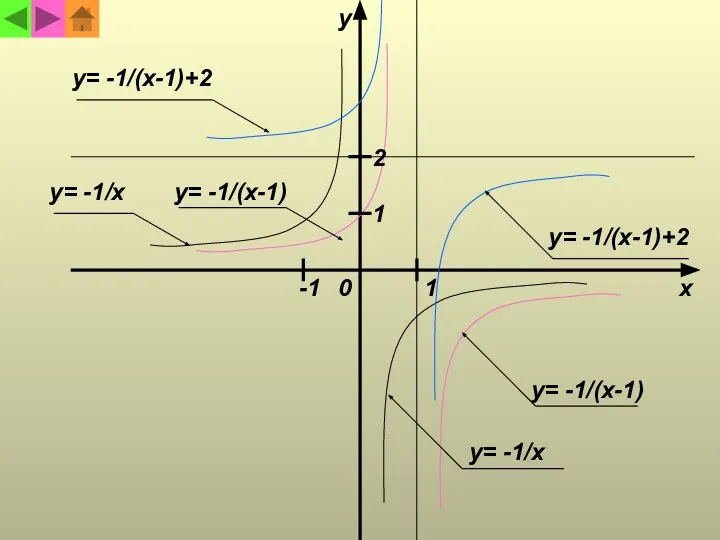
- 18. Пример 2 Построить график функции y = 3 - 2x 1 - x Решение. В данной
- 19. y= -1/x y= -1/x y= -1/(x-1) y= -1/(x-1)+2 1 1 y= -1/(x-1) y= -1/(x-1)+2 -1 2
- 21. Скачать презентацию





 Операции алгебры логики
Операции алгебры логики Решение задач с помощью уравнений. Урок математики в 5 классе
Решение задач с помощью уравнений. Урок математики в 5 классе Теория игр
Теория игр Равенство треугольников
Равенство треугольников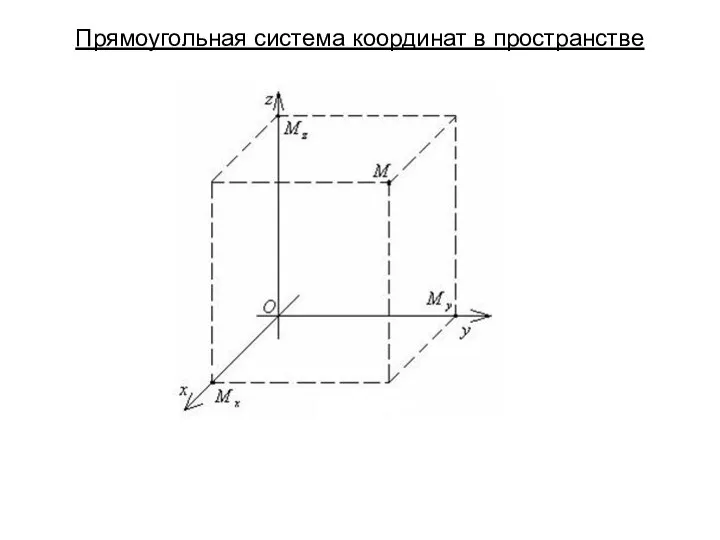 Прямоугольная система координат в пространстве. Понятие вектора
Прямоугольная система координат в пространстве. Понятие вектора Презентация на тему Квадрат суммы и квадрат разности (7 класс)
Презентация на тему Квадрат суммы и квадрат разности (7 класс)  Признаки существования предела
Признаки существования предела Площади фигур. 8 класс
Площади фигур. 8 класс Обобщение пропорции и лекарственные растения Сибири
Обобщение пропорции и лекарственные растения Сибири Презентация по математике "Письменные приёмы умножения" -
Презентация по математике "Письменные приёмы умножения" -  Анализ задач и альтернативные методы решений. Мастер-класс
Анализ задач и альтернативные методы решений. Мастер-класс Сложение чисел с разными знаками
Сложение чисел с разными знаками Обобщающий урок по начертательной геометрии прямая. Плоскость
Обобщающий урок по начертательной геометрии прямая. Плоскость Декартова система координат в пространстве
Декартова система координат в пространстве Луч. Дополнительные лучи. 5 класс
Луч. Дополнительные лучи. 5 класс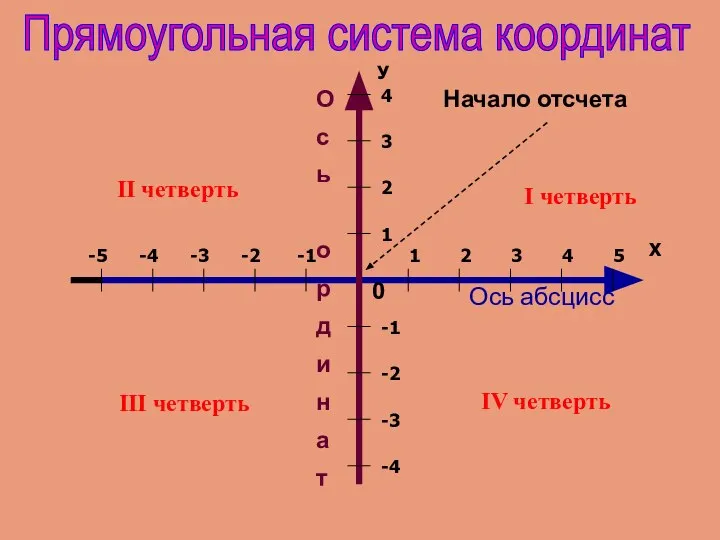 Ось абсцисс
Ось абсцисс Составление арифметических задач
Составление арифметических задач Алгоритм решения задач на нахождение слагаемых по сумме и разности
Алгоритм решения задач на нахождение слагаемых по сумме и разности Матрицы
Матрицы Декартова система координат на плоскости. Математика, 6 класс
Декартова система координат на плоскости. Математика, 6 класс Площадь круга и площадь кругового сегмента
Площадь круга и площадь кругового сегмента Решение задач по теме Объемы тел
Решение задач по теме Объемы тел Презентация на тему Геометрические построения в школьном курсе математики
Презентация на тему Геометрические построения в школьном курсе математики  Окружность
Окружность Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20)
Через точку А провести профильную прямую ВС, равнонаклоненную к плоскости П1 и плоскости П2. (задача 20) Решение уравнений методом замены переменной
Решение уравнений методом замены переменной Презентация на тему Теоремы синусов и косинусов
Презентация на тему Теоремы синусов и косинусов  Свойства квадратных корней
Свойства квадратных корней