- Главная
- Математика
- Квадратные уравнения ax² + bx + c = 0

Содержание
Слайд 21) ax² + bx = 0
Решение: x ( ax + b)
1) ax² + bx = 0
Решение: x ( ax + b)

= 0,
x = 0 или ax + b = 0, х =…
ax² + c = 0
Решение: ax² = - c, x² = - c/a, х = ….
ax² = 0
Решение : х = 0
x = 0 или ax + b = 0, х =…
ax² + c = 0
Решение: ax² = - c, x² = - c/a, х = ….
ax² = 0
Решение : х = 0
Неполные квадратные уравнения
Слайд 3
Решение квадратных уравнений
Решение квадратных уравнений

Слайд 4Если второй коэффициент b – четное число,
т. е. b = 2·k, то
Если второй коэффициент b – четное число,
т. е. b = 2·k, то

D/4 = D´ = k² - ac,
x = -k + √D´ и х = - k - √D´
x = -k + √D´ и х = - k - √D´
Решение квадратных уравнений по четверти дискриминанта
- Предыдущая
Коррекционная работа при параротацизме Четырехугольники. Решение задач
Четырехугольники. Решение задач Геометрические построения
Геометрические построения Прямая пропорциональность и ее график
Прямая пропорциональность и ее график Математическая викторина В гостях у мудрой совы 2 класс
Математическая викторина В гостях у мудрой совы 2 класс 8637
8637 Методы решения экстремальных задач
Методы решения экстремальных задач Экспресс-подготовка к ЗНО по математике
Экспресс-подготовка к ЗНО по математике Презентация на тему Тренажер - Табличное умножение и деление
Презентация на тему Тренажер - Табличное умножение и деление  Комплексные числа и координатная плоскость
Комплексные числа и координатная плоскость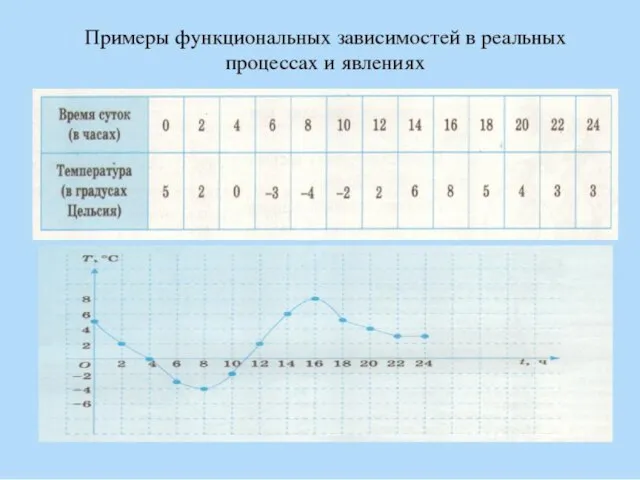 График функции. Примеры
График функции. Примеры Формула стоимости. Формула пути
Формула стоимости. Формула пути Квадратичная функция
Квадратичная функция Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8
Теория вероятностей и математическая статистика. Двумерные случайные величины. Лекция 8 Число и цифра 1. Часть 1
Число и цифра 1. Часть 1 Второй и третий признаки подобия треугольников
Второй и третий признаки подобия треугольников Функция и график
Функция и график Решение задач на построение. Трудность использования настоящего циркуля при изображении окружностей на доске
Решение задач на построение. Трудность использования настоящего циркуля при изображении окружностей на доске Презентация на тему Обратные тригонометрические функции
Презентация на тему Обратные тригонометрические функции  Многогранники. Призма
Многогранники. Призма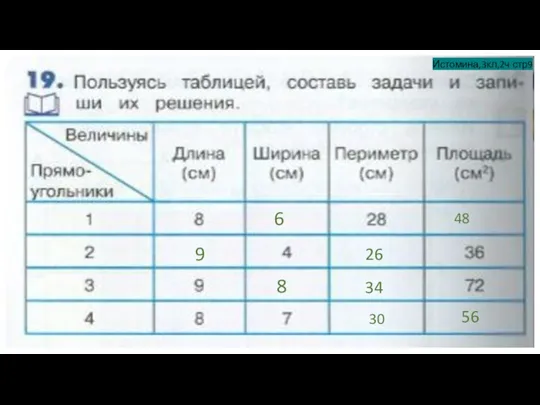 Величины. Составление задач
Величины. Составление задач Иррациональные неравенства
Иррациональные неравенства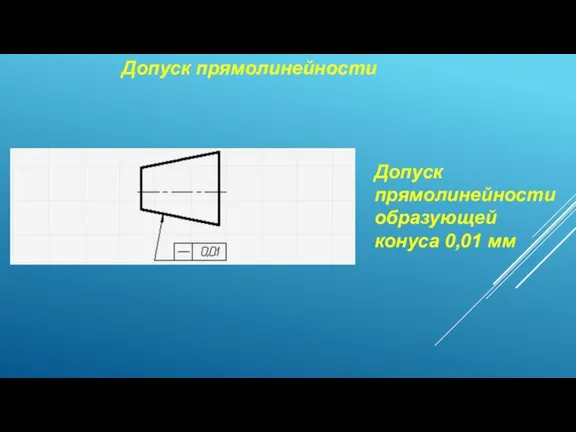 Допуск прямолинейности
Допуск прямолинейности Симметрия. Виды симметрии
Симметрия. Виды симметрии Признаки подобия треугольника
Признаки подобия треугольника Применение производной для исследования функций на монотонность и экстремумы
Применение производной для исследования функций на монотонность и экстремумы Приемы целеполагания
Приемы целеполагания Презентация на тему Внетабличное умножение и деление
Презентация на тему Внетабличное умножение и деление  Площадь параллелограмма
Площадь параллелограмма