Содержание
- 2. Математическая статистика - это наука и методах сбора, систематизации и обработке данных научных исследований с целью
- 3. Выборочный метод
- 4. Генеральная совокупность (ГС) – это вся подлежащая изучению совокупность объектов. Т.е., совокупность всех мыслимых наблюдений, которые
- 5. Генеральная совокупность аналогична случайной величине Х, поэтому она обладает законом распределения, математическим ожиданием, дисперсией и т.
- 6. Основная задача МС- исследовать ГС статистически, т.е., определение ее основных характеристик, закона распределения и т.п. Однако
- 7. Выборка Выборкой называется множество значений х1, х2, …, хn ГС , предназначенное для непосредственного исследования. Количество
- 8. Выборка Выборка бывает дискретной и непрерывной повторной и бесповторной, одномерной и многомерной.
- 9. Выборка Семинарское занятие - пример дискретной, повторной выборки. Диспансеризация спортсменов раз в полгода, измерение антропометрических данных
- 10. Выборка Результат измерения роста 20 человек. 176,5; 163,3; 173,4; 182,1; 152,3; 162,2; 200,0; 194,1; 154,4; 170,8;
- 11. Суть выборочного метода заключается в том, что на основании выборочных данных делается вывод о генеральной совокупности
- 12. Репрезентативность Для того, чтобы оценки полученные по выборочным данным были достоверными, необходимо, чтобы выборка была репрезентативной,
- 15. Варианты и частоты Наблюдаемое значение признака в статистике называется вариантой и обозначается хi. Одна и та
- 16. Вариационный ряд Если все значения признака записать в порядке возрастания или убывания , то такое представление
- 17. Выборка Выборка Упорядоченная выборка
- 18. Статистическое представление выборки Если значения вариант соответствуют значениям дискретной СВ, то она называется дискретной.
- 19. Статистическое представление выборки Статистическим представле-нием дискретной выборки называется таблица, в первой строке которой записывают значения вариант
- 20. Статистическое представление дискретной выборки (частоты)
- 21. Условие нормировки
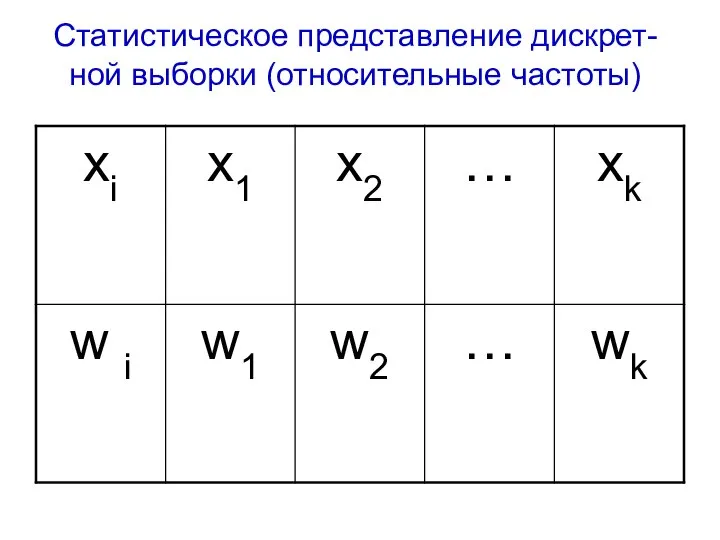
- 22. Статистическое представление дискрет-ной выборки (относительные частоты)
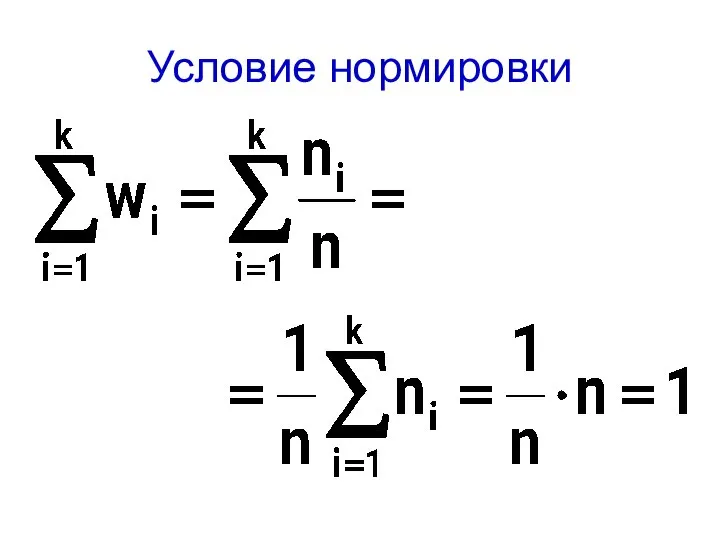
- 23. Условие нормировки
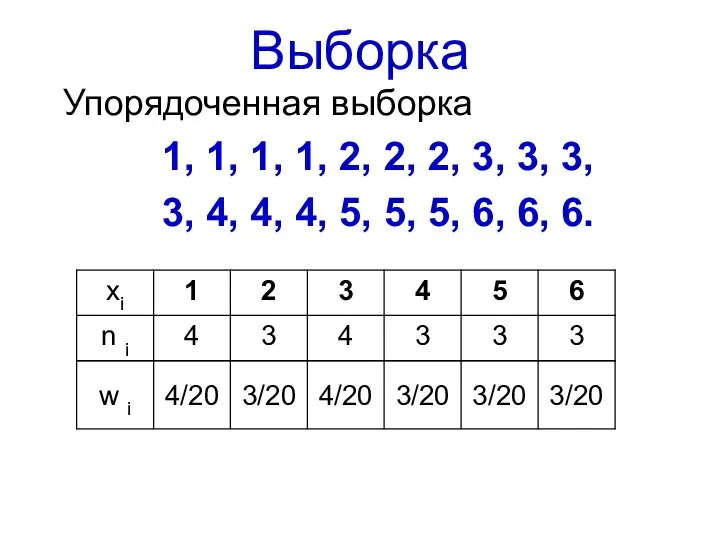
- 24. Выборка Упорядоченная выборка 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 4, 4,
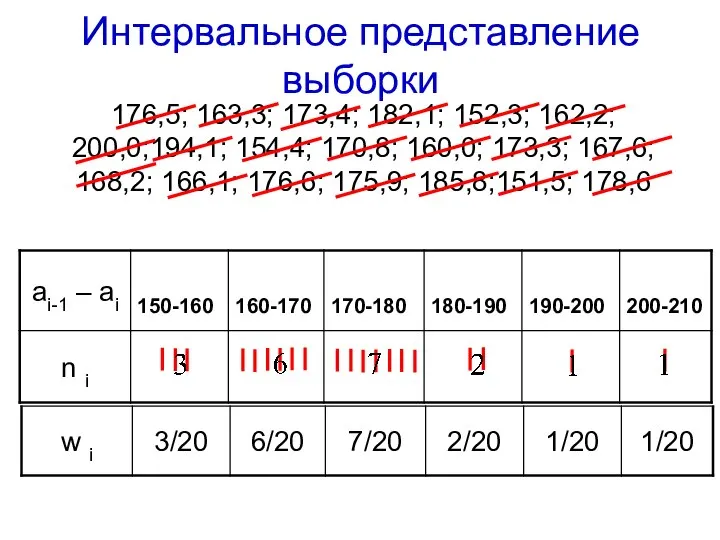
- 25. Интервальное представление выборки Если в выборке имеется большое количество различных значений признака, то ее удобно представлять
- 26. Интервальное представление выборки Частота i-го частичного интервала ni – определяется путем подсчета объектов выборки, значения которых
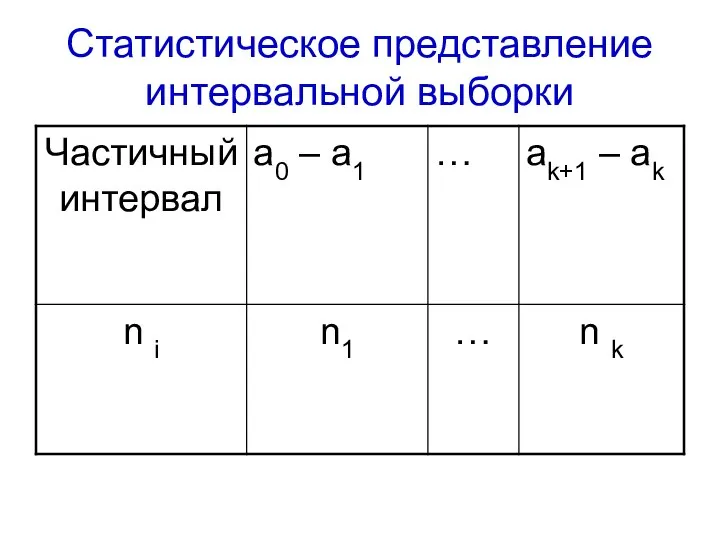
- 27. Статистическое представление интервальной выборки
- 28. Пример Результат измерения роста 20 человек (n = 20). 176,5; 163,3; 173,4; 182,1; 152,3; 162,2; 201,0;194,1;
- 29. Интервальное представление выборки 176,5; 163,3; 173,4; 182,1; 152,3; 162,2; 200,0;194,1; 154,4; 170,8; 160,0; 173,3; 167,6; 168,2;
- 30. Накопленные частоты Накопленной частотой i-ой варианты – называется количество объектов выборки, значение которых не превосходит хi
- 31. Накопленные частоты Относительной накопленной частотой i-ой группы выборки – называется число
- 32. Графические представления выборки Графически выборку можно представить в виде: полигона, гистограммы и кумуляты. .
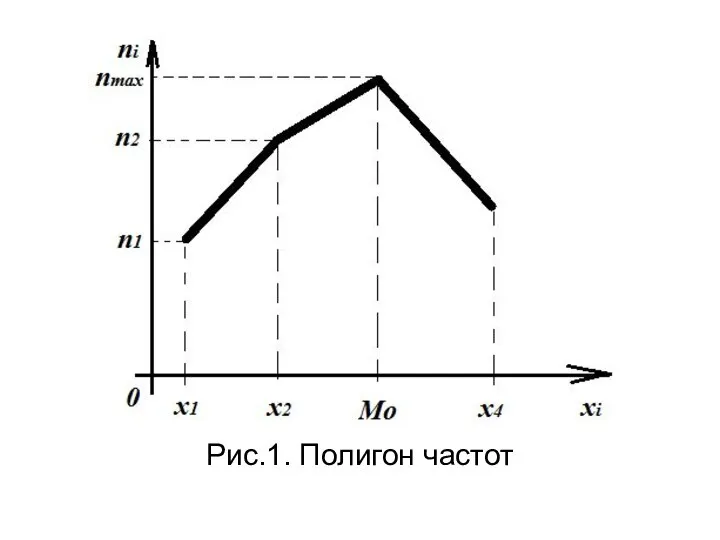
- 33. Полигон частот- это ломаная линия, отрезки которой соединяют вершины (x i, n i) или (х i,
- 34. Рис.1. Полигон частот
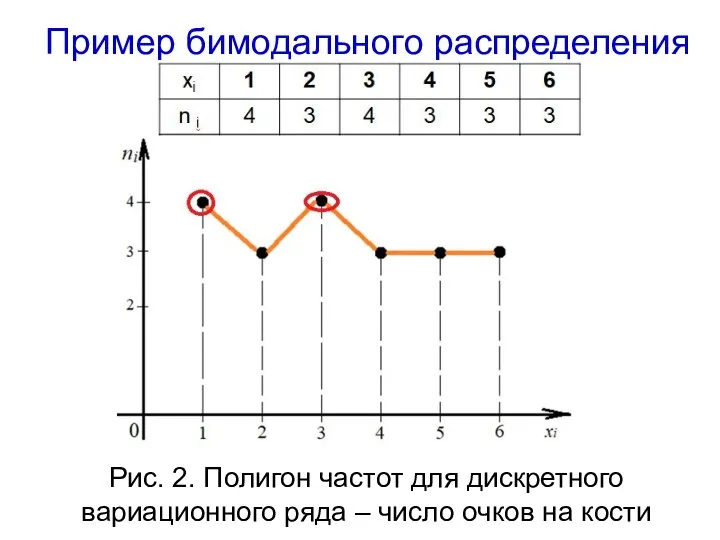
- 35. Пример бимодального распределения Рис. 2. Полигон частот для дискретного вариационного ряда – число очков на кости
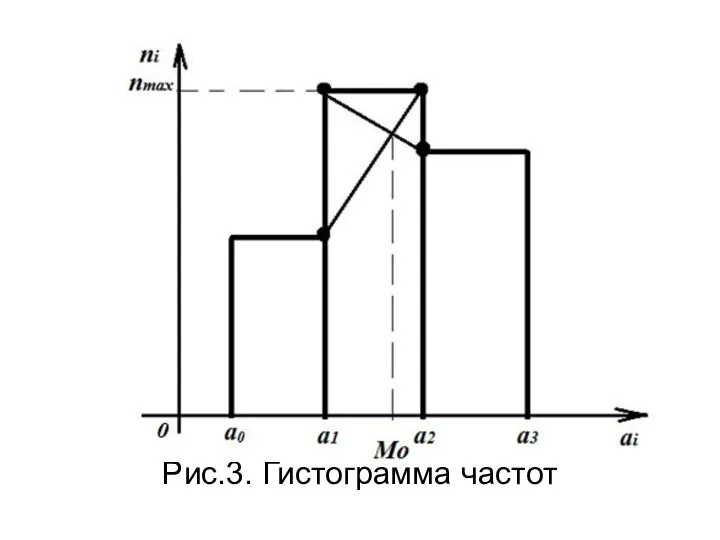
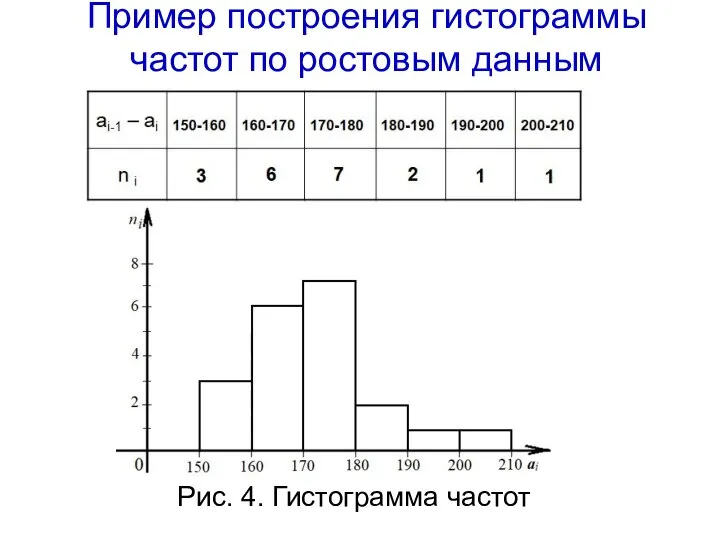
- 36. Гистограмма частот- это множество прямоугольников, в основании которых лежат частичные интервалы, а высоты соответствуют частоте (относительной
- 37. Рис.3. Гистограмма частот
- 38. Гистограмма относительных частот При построении гистограммы относительных частот высоты прямоугольников соответствуют относительной частоте. Если интервалы имеют
- 39. Рис. 4. Гистограмма частот Пример построения гистограммы частот по ростовым данным
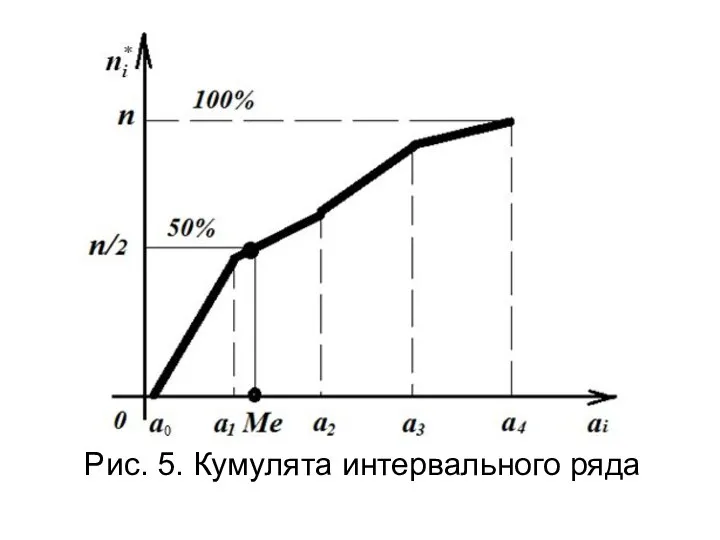
- 40. Кумулята – это ломаная линия, отрезки которой соединяют точки (xi,ni⁕)-(значение варианты, значение накопленной частоты). По кумуляте
- 41. Рис. 5. Кумулята интервального ряда
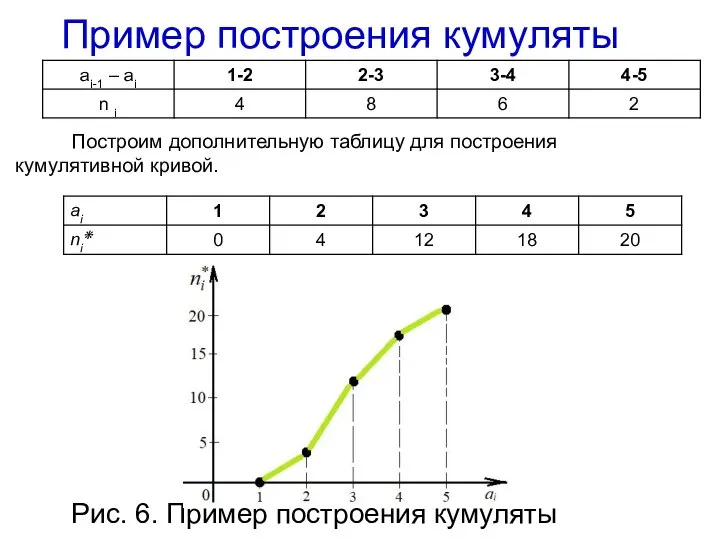
- 42. Пример построения кумуляты Построим дополнительную таблицу для построения кумулятивной кривой. Рис. 6. Пример построения кумуляты
- 43. Эмпирическая функция распределения Эмпирическая функция распределения находится по формуле: Здесь n – это объем выборки; nх-
- 44. Свойства функции эмпирической функции распределения 1. 2. неубывающая функция, то есть 3. Эмпирическая функция распределения –
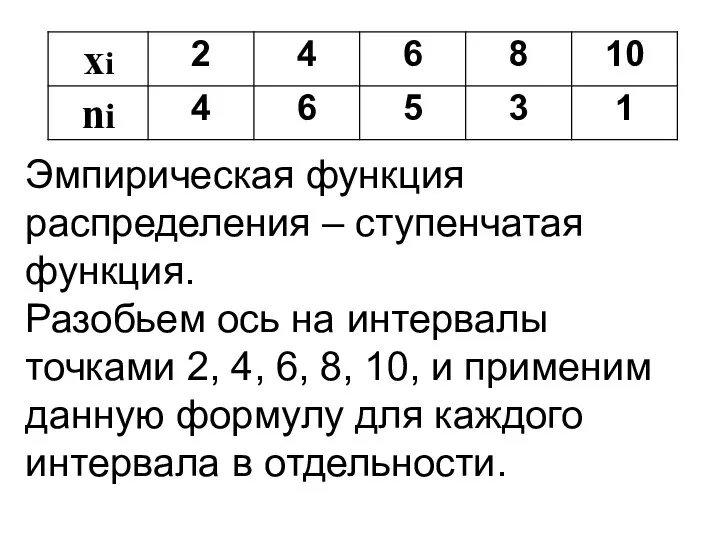
- 45. Найдем объем выборки.
- 46. Эмпирическая функция распределения – ступенчатая функция. Разобьем ось на интервалы точками 2, 4, 6, 8, 10,
- 47. 1)
- 48. 2)
- 49. 3)
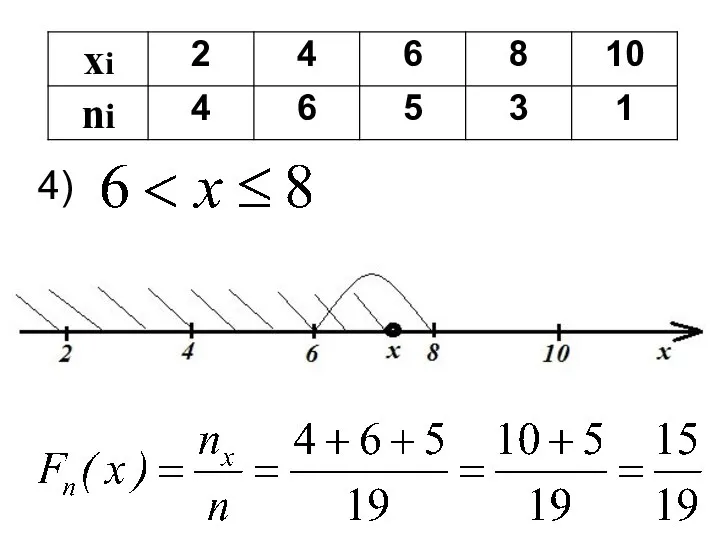
- 50. 4)
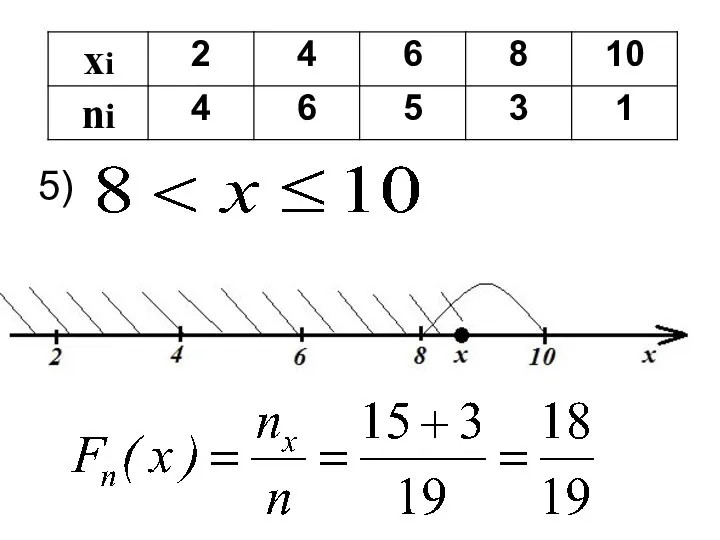
- 51. 5)
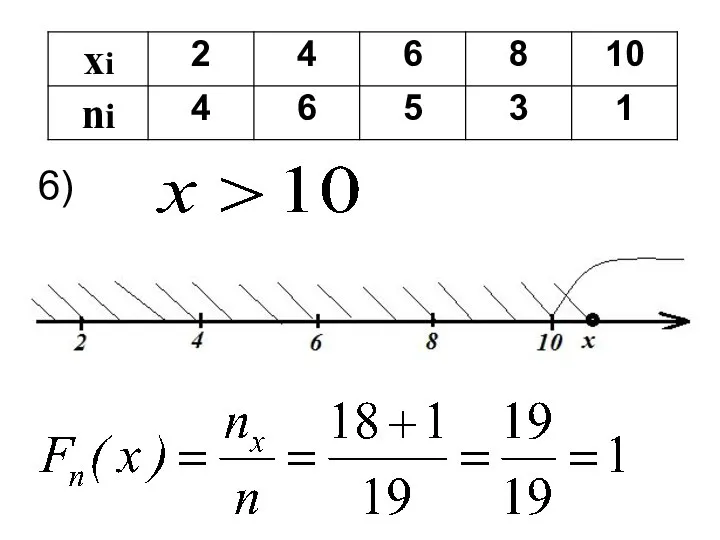
- 52. 6)
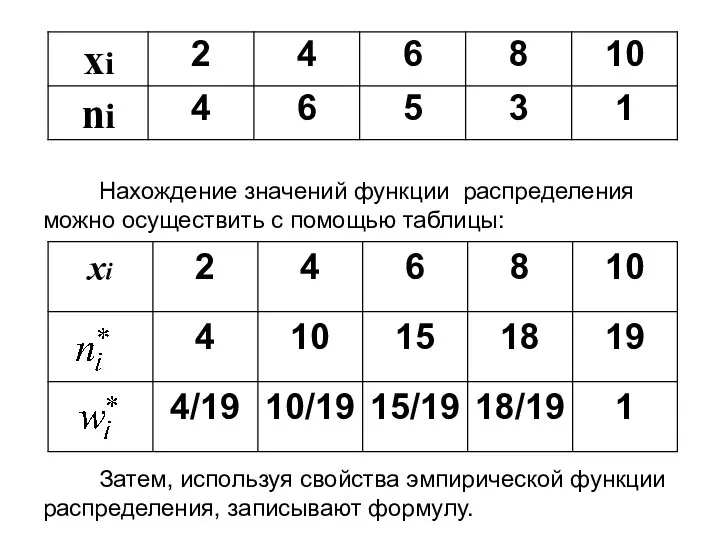
- 54. Нахождение значений функции распределения можно осуществить с помощью таблицы: Затем, используя свойства эмпирической функции распределения, записывают
- 56. Скачать презентацию




































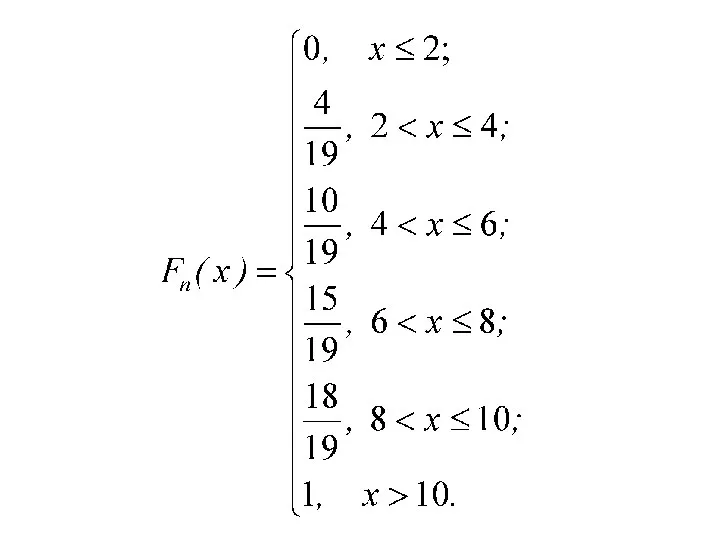
 Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма
Государственное общеобразовательное учреждение Гимназия№49 Приморского района Санкт -Петербурга «Путешествие Алисы в страну Ма Основы функционального анализа
Основы функционального анализа Алгебраические и геометрические модели
Алгебраические и геометрические модели Прямая и окружность
Прямая и окружность Решение задач на построение методом подобных треугольников
Решение задач на построение методом подобных треугольников Построение треугольника
Построение треугольника Векторы. Обобщающий урок
Векторы. Обобщающий урок Решение логарифмических уравнений
Решение логарифмических уравнений Уравнение древности. Франсуа Виет
Уравнение древности. Франсуа Виет Решение уравнений и неравенств с модулем
Решение уравнений и неравенств с модулем Решение задач на применение аксиом стереометрии и их следствий
Решение задач на применение аксиом стереометрии и их следствий Параллелепипед. Куб
Параллелепипед. Куб Элементы комбинаторики
Элементы комбинаторики Решение начально-краевой задачи для линейного уравнения теплопроводности разностным методом. Практическое занятие №8
Решение начально-краевой задачи для линейного уравнения теплопроводности разностным методом. Практическое занятие №8 Шар и сфера
Шар и сфера Нумерация. Сложение и вычитание. Геометрические фигуры и величины
Нумерация. Сложение и вычитание. Геометрические фигуры и величины Диференціальні рівняння
Диференціальні рівняння Отрезок, луч, прямая. Графический диктант 1. 5 класс
Отрезок, луч, прямая. Графический диктант 1. 5 класс Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ
Презентация на тему ДЕЛИТЕЛИ И КРАТНЫЕ  Формулы сокращенного умножения a b
Формулы сокращенного умножения a b Знакомство с линейкой, единицей измерения длины – сантиметр (2 урок)
Знакомство с линейкой, единицей измерения длины – сантиметр (2 урок) Дискретные случайные величины
Дискретные случайные величины Применение математики в нематематических областях
Применение математики в нематематических областях Решение задач
Решение задач Линейная функция и ее график
Линейная функция и ее график Математика (1 класс)
Математика (1 класс) Методы кластеризации
Методы кластеризации Презентация на тему Русская система мер
Презентация на тему Русская система мер