Слайд 2Задача 1
В партии из 10 выключателей 3 бракованных.
Из этой партии наугад выбирают

3 выключателя.
Найти вероятность того, что ровно 1 выключатель в данной выборке будет бракованным.
Слайд 3Решение
р = m/n
m – число благоприятных исходов;
n – число всех исходов.
Наиболее просто

рассчитывается число всех исходов n.
n показывает, сколькими способами можно взять 3 выключателя из 10:
n = C103 = 120.
m показывает, сколькими способами можно выбрать ровно 1 бракованный выключатель;
другими словами, сколькими способами можно выбрать 1 бракованный выключатель из 3 и одновременно 2 исправных выключателя из 7:
m = C31 · C72 = 63.
р = 63/120 = 0,525.
Слайд 4Задача 2
Из 10 изоляторов дефектными являются 2.
Какова вероятность того, что среди

взятых случайных образом 5 изоляторов ровно 1 окажется дефектным?



 Логарифмические уравнения. Обобщающий урок
Логарифмические уравнения. Обобщающий урок Система упражнений по изучению свойств линейной функции
Система упражнений по изучению свойств линейной функции Табличное умножение и деление. Решение задач изученных видов. 3 класс
Табличное умножение и деление. Решение задач изученных видов. 3 класс Тренажёр Именованные числа. 4 класс
Тренажёр Именованные числа. 4 класс Презентация на тему Сложение чисел с разными знаками (6 класс)
Презентация на тему Сложение чисел с разными знаками (6 класс)  Стереометрия. Основные понятия стереометрии. Аксиомы стереометрии
Стереометрия. Основные понятия стереометрии. Аксиомы стереометрии Прохождение случайной волны через отверстие в экране. Теорема Ван-Циттерта-Цернике
Прохождение случайной волны через отверстие в экране. Теорема Ван-Циттерта-Цернике Статистическая проверка гипотез
Статистическая проверка гипотез Додавання і віднімання мішаних чисел
Додавання і віднімання мішаних чисел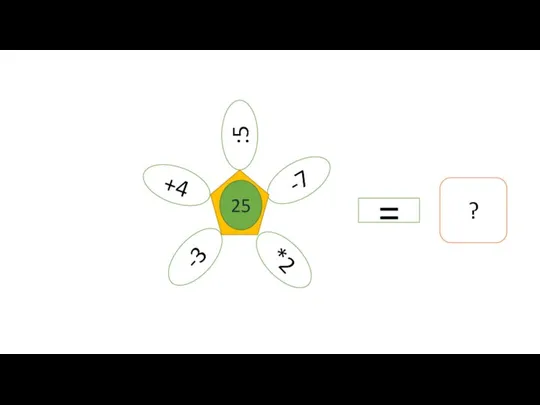 Ромашка
Ромашка Окружность и круг
Окружность и круг Планиметрия. Решение прямоугольного треугольника
Планиметрия. Решение прямоугольного треугольника Автоматизация ректификационной колонны К-2 установки сернокислотного алкилирования Л-25/7
Автоматизация ректификационной колонны К-2 установки сернокислотного алкилирования Л-25/7 Пределы. Раскрытие неопределенности. 2 часть
Пределы. Раскрытие неопределенности. 2 часть Окружность. Элементы окружности. Формулы
Окружность. Элементы окружности. Формулы Вероятность события. Разбор задач
Вероятность события. Разбор задач Ромб, квадрат. Ответы на вопросы
Ромб, квадрат. Ответы на вопросы Случайность. Массовые явления
Случайность. Массовые явления Решение задач по теме: Прямоугольник. Ромб. Квадрат
Решение задач по теме: Прямоугольник. Ромб. Квадрат Найдите наименьшее (наибольшее) значение функции на промежутке
Найдите наименьшее (наибольшее) значение функции на промежутке Смеси и сплавы в задачах №13 ЕГЭ-2015 г
Смеси и сплавы в задачах №13 ЕГЭ-2015 г Японские числительные
Японские числительные Математика здесь!
Математика здесь! Способы решения систем линейных уравнений
Способы решения систем линейных уравнений Решение тригонометрических уравнений
Решение тригонометрических уравнений Решение иррациональных неравенств
Решение иррациональных неравенств Стереометрія. Аксіоми стереометрії
Стереометрія. Аксіоми стереометрії Путешествие в страну Геометрию
Путешествие в страну Геометрию