Содержание
- 2. Розглянемо задачу про поширення періодичного граничного режиму: або Відповідно знайдемо вирішення задачі: Нехай З 1ї граничної
- 3. Переходимо до границі α –> 0: Розглянемо наступну задачу: ? a = 0 a ≠ 0
- 4. Для а = 0 рішення визначено неоднозначно, якщо не накладати додаткових умов Для отримання одного рішення
- 5. Єдиність обмеженого розв’язку Припустимо неперервність рішень із похідними до 2го порядку включно в області При цьому
- 7. Скачать презентацию




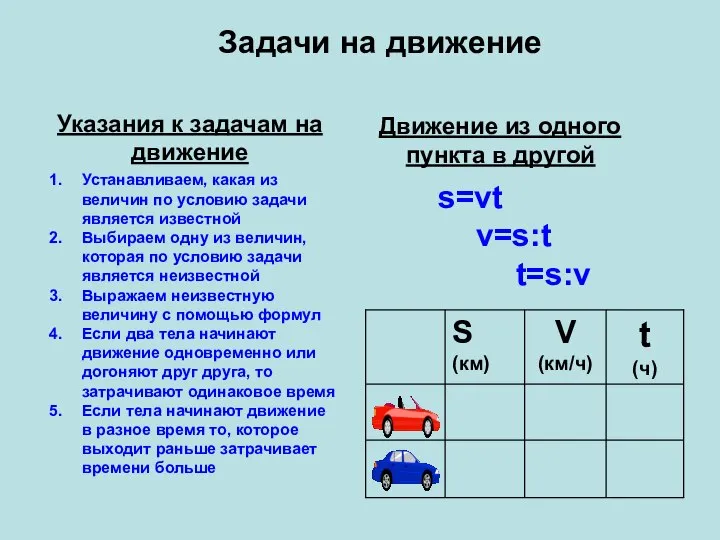 Задачи на движение Указания к задачам на движение
Задачи на движение Указания к задачам на движение Пустое множество
Пустое множество Решение задача на совместную работу. 6 класс
Решение задача на совместную работу. 6 класс Длина окружности. Лабораторная работа
Длина окружности. Лабораторная работа Метод интервалов. 8 класс
Метод интервалов. 8 класс Векторы. Действия с векторами
Векторы. Действия с векторами Решение задач на проценты
Решение задач на проценты Построение биссектрисы угла. Билеты
Построение биссектрисы угла. Билеты Сравнение десятичных дробей. Работа по учебнику
Сравнение десятичных дробей. Работа по учебнику Подготовка к ЕГЭ В8
Подготовка к ЕГЭ В8 Координатная плоскость
Координатная плоскость Прямоугольный параллелепипед
Прямоугольный параллелепипед Random module methods. Test
Random module methods. Test Анализ геометрической формы предмета
Анализ геометрической формы предмета Наши проекты. Оригами Странички для любознательных
Наши проекты. Оригами Странички для любознательных Симетричні фігури
Симетричні фігури Число и цифра 5
Число и цифра 5 Итоговая диагностика. Математическая вертикаль. 8 класс
Итоговая диагностика. Математическая вертикаль. 8 класс Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл.
Урок по теме Математика 6 класс Подготовлено Гаенко Т.А. Акимовская школа №3 Запорожской обл. Вариационные ряды и их характеристики. Глава 3. Элементы математической статистики
Вариационные ряды и их характеристики. Глава 3. Элементы математической статистики Презентация на тему Описательная статистика
Презентация на тему Описательная статистика  Показательные уравнения
Показательные уравнения Пирамида Кукулькана – величайший храм майя
Пирамида Кукулькана – величайший храм майя Федеральный интернет-экзамен. Дифференцирование
Федеральный интернет-экзамен. Дифференцирование Без слов и грамматики не учат математике
Без слов и грамматики не учат математике Уравнение прямой на плоскости
Уравнение прямой на плоскости Как лгать при помоощи статистики
Как лгать при помоощи статистики Частные производные второго порядка
Частные производные второго порядка