Задачи с параметром в материалах Государственной итоговой аттестации и методы их решения (По материалам ЕГЭ за последние 5лет)

Изучение задач с параметрами в материалах государственной итоговой аттестации и методов их решения.
Цель:
Задачи:
1. Провести теоретический анализ литературы по данной теме;
2. Дать определение параметра, рассмотреть типы задач с параметром; выделить основные методы их решения;
3. Подобрать серию задач с параметром, решаемых с помощью основных методов.

В последние годы задачи с параметрами постоянно содержатся в заданиях Государственной итоговой аттестации по математике, а умение решать данные задачи во многом является залогом достижения высокого экзаменационного балла. Данные задачи позволяют проверить владение формулами элементарной математики, методами решения уравнений и неравенств, определить навыки математической исследовательской деятельности, уровень логического мышления учащегося.
Введение:

Определение понятия «параметр» и «задача с параметром»
Параметр – это независимая переменная, значение которой в данной задаче считается фиксированным.
Задача, условие которой содержит или в ходе решения которой появляется хотя бы одна независимая переменная, удовлетворяющая определению понятия «параметр», называется задачей с параметрами.

Типы задач с параметром, встречающиеся в материалах Государственной итоговой аттестации
1) Найти все значения параметра, для каждого из которых выполняются те или иные условия (уравнение, неравенство или система имеют определённое число решений; решение принадлежит определённому множеству или удовлетворяет определённым ограничениям и т. п.; сами решения находить при этом, как правило, не требуется).
Пример. Найдите все значения a, при каждом из которых уравнение
имеет корни, но ни один из них не принадлежит интервалу (4;19).

2) Найти все значения параметра, при каждом из которых задача имеет хотя бы одно решение, и указать эти решения для каждого такого значения параметра (кратко: «при каждом значении параметра решить уравнение (неравенство, систему)».
Типы задач с параметром, встречающиеся в материалах Государственной итоговой аттестации
Пример. При каждом значении параметра a решить неравенство

Рассмотрев и сравнив задачи с параметром из вариантов демоверсий ФИПИ, досрочного и основного этапа ЕГЭ за последние пять лет можно сделать выводы о том, что задачи с параметром демоверсий ФИПИ во всех случаях совпадают с задачами досрочного и основного этапа ЕГЭ и относятся к первому типу, описанному нами выше.
Сравнительный анализ задач с параметром демоверсий ЕГЭ по математике ФИПИ с вариантами досрочного и основного этапа ЕГЭ

Аналитический метод
Основной частью аналитического метода решения задач является метод эквивалентных или равносильных преобразований. Предлагаемый подход к решению уравнений и неравенств с параметрами, их систем или совокупностей основан на замене одного математического высказывания другим равносильным математическим высказыванием. Задача рассматривается как некоторое логическое высказывание, область истинности которого предстоит установить в результате его рассмотрения. При этом исходное условие рядом равносильных преобразований или преобразований следствий приводится к совокупности простейших логических утверждений, истинность или ложность которых считается установленной.
В аналитическом методе решения задач чаще всего используется приём дробления – разделение условия задачи на совокупность более простых условий.

Решение:
При a=1 уравнение не имеет корней
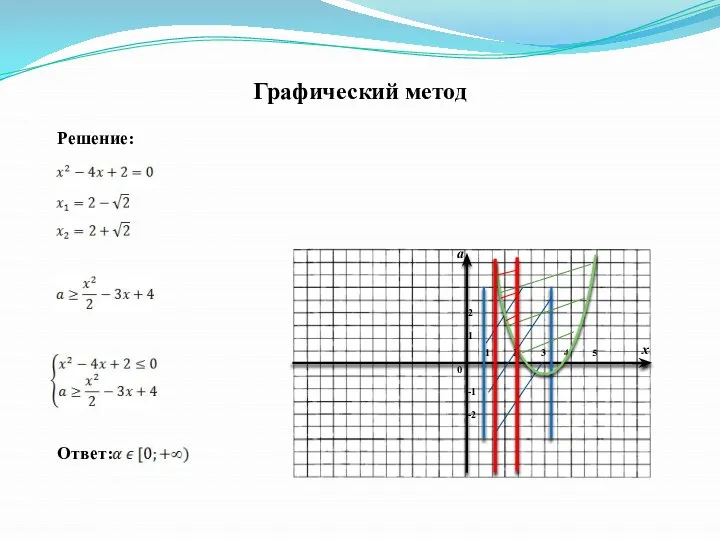
При a 1
.

Графический метод
Любая задача с параметрами есть задача как минимум с двумя переменными – аргументом и параметром. Следовательно, решение задачи - упорядоченный набор их значений, может рассматриваться как координаты точки некоторого евклидова пространства. Данный метод лучше всего работает, если условие задачи содержит вопрос о количестве корней в зависимости от значений параметра или определения значений параметра, при которых решение отсутствует или единственно.

.

Цель данной работы состояла в изучении задач с параметрами в материалах государственной итоговой аттестации и методов их решения.
Изучив и проанализировав задачи с параметрами в материалах ЕГЭ по математике за последние пять лет, было выявлено, что в большинстве случаев встречаются задачи первого типа рассмотренной нами классификации. Для решения этих задач в основном используются аналитический и графический методы.
Для закрепления навыков решения задач с параметром была подобрана серия данных задач.
Таким образом, задачи выполнены, цель работы достигнута.
Заключение: