Жизнь и творчество Сальвадора Дали и его картины с математическими загадками

«Математика-это искусство
называть разные вещи одним
и тем и тем же именем»
Анри Пуанкаре

Математика – это не только стройная система законов, теорем, задач, но и уникальное средство познания красоты. А красота многогранна и многолика. Она выражает высшую целесообразность устройства мира, подтверждает универсальность математических закономерностей, которые действуют одинаково эффективно в кристаллах и в живых организмах, в атомах и во Вселенной, в произведениях искусства и научных открытиях.

Красота помогает с радостью воспринимать окружающий мир, математика даёт возможность осознать явления и упрочить знания о гармонии всего мира.
Изучая математику, мы открываем всё новые и новые слагаемые красоты, приближаясь к пониманию, а затем и к созданию красоты и гармонии.
Когда раскрывается эффективность применения математических методов в различных областях науки, культуры, искусства, не ущемляется роль математики, не подменяется другими предметами, а, наоборот, повышается интерес к предмету, выявляется высокое значение математики, процесс познания её делается увлекательным.

“Ничто не нравится, кроме красоты, в красоте – ничто, кроме форм, в формах – ничто, кроме пропорций, в пропорциях – ничто, кроме числа”. А. Августин

Исторически, математика играла важную роль в изобразительном искусстве.
Согласно современным взглядам, математика и изобразительное искусство очень удаленные друг от друга дисциплины, первая - аналитическая, вторая - эмоциональная.
Математика не играет очевидной роли в большинстве работ современного искусства, и, фактически, многие художники редко или вообще никогда не используют даже использование перспективы. Однако, есть много художников, у которых математика находится в центре внимания.

Морис Корнелис Эшер
(1898-1972)
Голландский художник М.К. Эшер в некотором роде является отцом математического искусства.
В период с 1950 по 1960 годы он создал свои наиболее известные картины в том числе и с невозможными конструкциями.

Творчество Эшера оказало огромное влияние на несчетное количество художников в разных странах мира. Работы Эшера являются наиболее излюбленными среди математиков, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов. Это более интересно тем, что сам Эшер не имел специального математического образования.
В процессе своей работы он черпал идеи из математических статьей, в которых рассказывалось о мозаичном разбиении плоскости, проецировании трехмерных фигур на плоскость и неевклидовой геометрии.

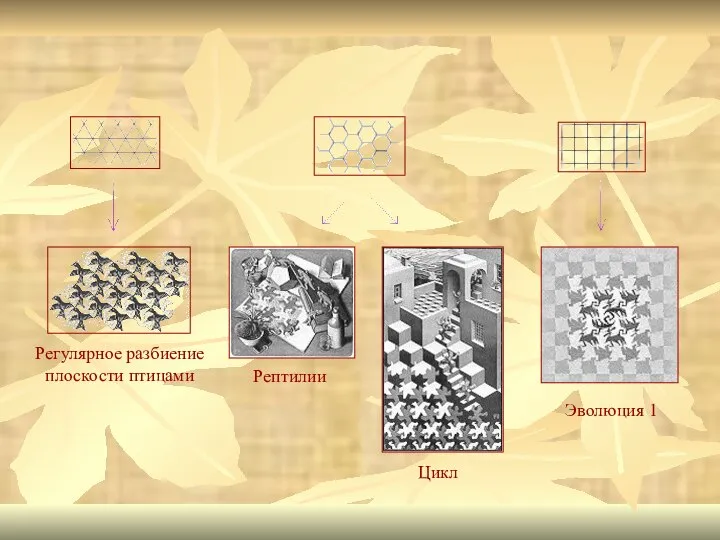
Регулярное разбиение плоскости, называемое "мозаикой" - это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними.
Эскиз из Альгамбры
Мозаики

Интересоваться мозаиками Эшер начал в 1936 году во время путешествия по Испании. Он провел много времени в Альгамбре, зарисовывая арабские мозаики, и впоследствии сказал, что это было для него "богатейшим источником вдохновения". Позже в 1957 году в своем эссе о мозаиках Эшер написал: В математических работах регулярное разбиение плоскости рассматривается теоретически... Значит ли это, что данный вопрос является сугубо математическим? Математики открыли дверь ведущую в другой мир, но сами войти в этот мир не решились. Их больше интересует путь, на котором стоит дверь, чем сад, лежащий за ней.

Математики доказали, что для регулярного разбиения плоскости подходят только три правильных многоугольника: треугольник, квадрат и шестиугольник. Эшер использовал базовые образцы мозаик, применяя к ним трансформации, которые в геометрии называются симметрией, отражение, смещение и др. Также он исказил базовые фигуры, превратив их в животных, птиц, ящериц и проч. Эти искаженные образцы мозаик имели трех-, четырех- и шестинаправленную симметрию, таким образом сохраняя свойство заполнения плоскости без перекрытий и щелей.

Регулярное разбиение
плоскости птицами
Рептилии
Цикл
Эволюция 1

Правильные геометрические тела - многогранники - имели особое очарование для Эшера. Во его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.
Многогранники

2. Леонардо да Винчи (1452-1519)
Леонардо да Винчи известен своими достижениями в качестве изобретателя и художника. В его записных книгах содержатся первые из известных примеров анаморфного искусства, использующего искаженные сетки перспективы. Его наклонные анаморфные изображения представляют объекты, которые должны рассматриваться по углом, чтобы они выглядели неискаженными.

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

Золотое сечение
Леонардо да Винчи – одна из загадок истории. Сам Леонардо да Винчи говорил: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”.
Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует очень много версий об истории этого портрета. Вот одна из них.
Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекала простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.

Леонардо да Винчи "Джоконда"
Портрет Моны Лизы привлекает тем, что композиция рисунка построена на"золотых треугольниках" (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).

6. Сальвадор Дали (1904-1989)
Сальвадор Дали - яркий и парадоксальный испанский художник использовал математические идеи в некоторых своих картинах.
На картине "Распятие" (1954) изображен Иисус распятый на развертке тессеракта (гиперкубе).

"Плоть на камнях"
картина, написанная в 1926 году.
Данное полотно выполнено в несвойственной Сальвадору кубистической манере.

«Постоянство памяти» 1931г
Дали толковал гибкие часы как символ четырехмерного непрерывного пространства

Гиперкуб
В геометрии гиперкуб - это n-мерная аналогия квадрата (n = 2) и куба (n = 3). Это замкнутая выпуклая фигура, состоящая из групп параллельных линий, расположенных на противоположных краях фигуры, и соединенных друг с другом под прямым углом.
Эта фигура также известная под названием тессеракт. Тессеракт относится к кубу, как куб относится к квадрату. Более формально, тессеракт может быть описан как правильный выпуклый четырехмерный политоп (многогранник), чья граница состоит из восьми кубических ячеек.
Проекция куба на плоскость

Тессеракт может быть развернут в восемь кубов, подобно тому как куб может быть развернут в шесть квадратов. Многогранник-развертка гиперкуба называется сетью. Существует 261 различных вариантов сетей. Справа показан один из вариантов
Развертка тессеракта

Математика и физика в работах художника

Больше всего его увлекала проблема баланса в кажущемся отсутствии порядка, а в квантовом мире его интересовала пульсирующая мысль, увлекаемая вихрем неизведанного, что подразумевало решительный и кардинальный пересмотр сложившихся представлений. И порождало множество сомнений.
Одна из его работ , как раз , посвящена открытиям в области квантовой физики

Дали преподнес Пию XII один из вариантов своей картины «Мадонна Порт-Льигата», написанной по мотивам «Пресвятой Девы с младенцем в окружении ангелов и святых» Пьеро делла Франчески 14 и под впечатлением от открытий в области квантовой физики, от антиматерии и расщепления атома...

ДЖЕЙМС ТРЭЛЛ СОБИ
«Дали — это хищная рыба, которая рыщет в холодных водах искусства и теплых водах науки».

В заключении, хотелось бы сказать, что таким гением , который еще раз подтвердил, искусство не может существовать без научного фундамента и наоборот стал Сальвадор Дали.
Наука поглотила его .Все работы в той или иной степени относятся к научным открытиям того времени.
Дали подчеркнул простую истину, что быть просто художником мало- нужно быть немного "чокнутым "гением.

Спасибо за внимание !