Содержание
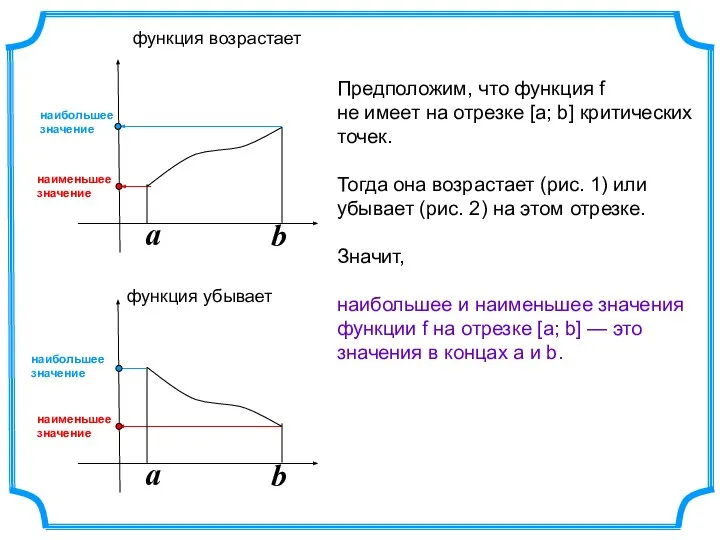
- 2. a b a b Предположим, что функция f не имеет на отрезке [а; b] критических точек.
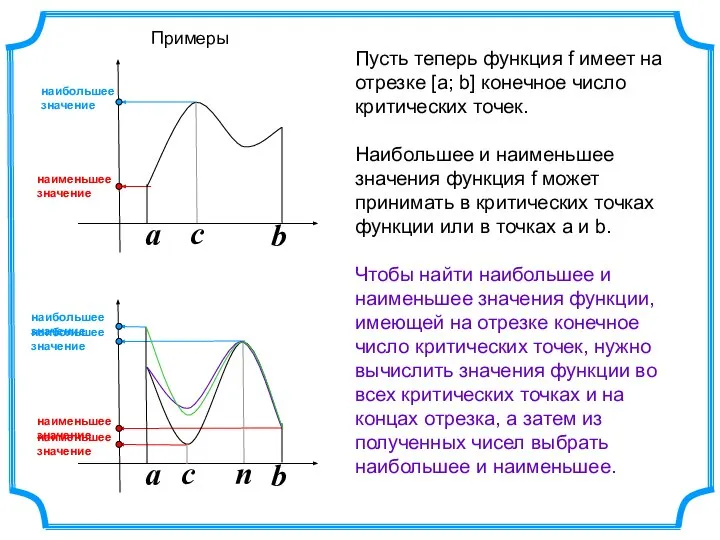
- 3. a b a b Пусть теперь функция f имеет на отрезке [а; b] конечное число критических
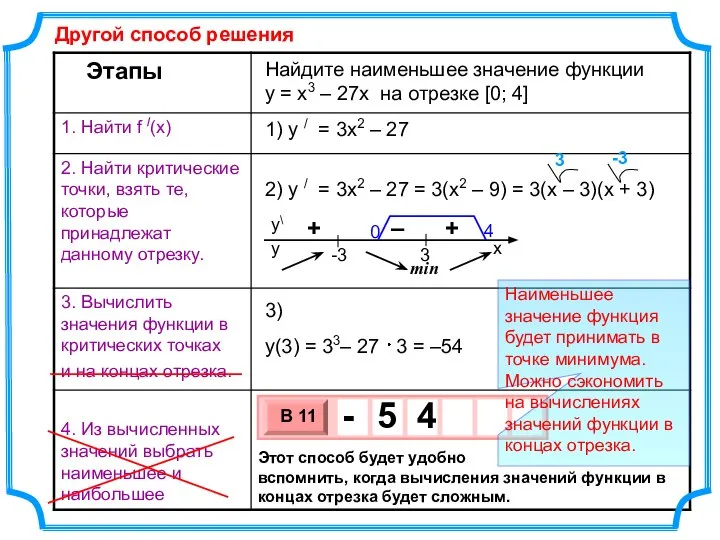
- 4. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1. Найдем критические
- 5. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1) y /
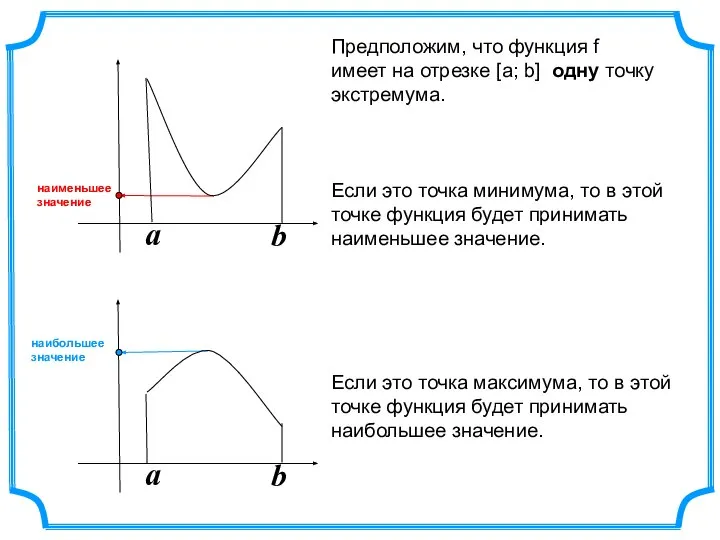
- 6. a b a b Предположим, что функция f имеет на отрезке [а; b] одну точку экстремума.
- 7. Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4] 1) y /
- 8. Найдем критические точки, которые принадлежат заданному отрезку. Выбрать наибольшее из полученных значений. 1) y(0) = 4
- 9. Найдем критические точки, которые принадлежат заданному отрезку. Выбрать наименьшее из полученных значений. 1) y(1) = 1
- 10. Найдите наибольшее значение функции на отрезке [ -3; 3 ] 4. Найдем критические точки, которые принадлежат
- 11. Найдите наибольшее значение функции на отрезке [ 1; 9 ] 5. Найдем критические точки, которые принадлежат
- 12. Найдите наименьшее значение функции на отрезке [ 1; 9 ] 6. Найдем критические точки, которые принадлежат
- 13. Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические точки, которые принадлежат заданному
- 14. Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические точки, которые принадлежат заданному
- 15. Найдите наибольшее значение функции на отрезке [ 1; 9 ] 8. Найдем критические точки, которые принадлежат
- 16. Найдите наибольшее значение функции на отрезке [ 3; 10 ] 9. Найдем критические точки, которые принадлежат
- 17. Найдите наименьшее значение функции на отрезке [ 1; 7 ] 10. Найдем критические точки, которые принадлежат
- 18. Найдите наибольшее значение функции y = ln(x+5)5 – 5x на отрезке [-4,5; 0] 11. max Наибольшее
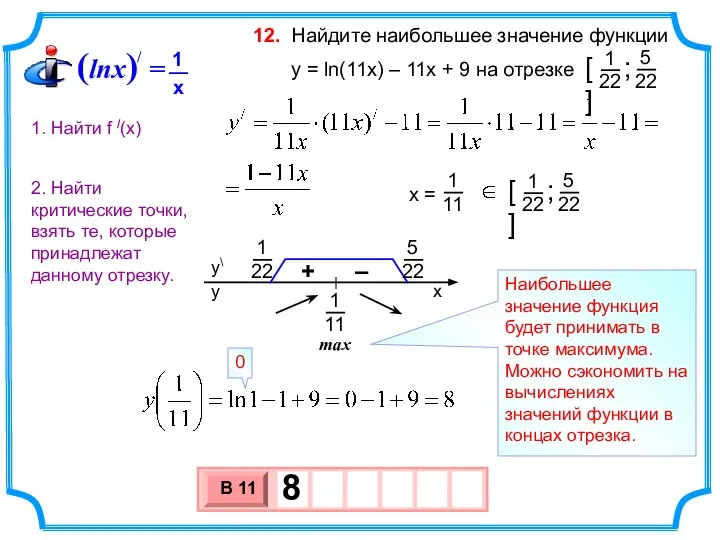
- 19. Найдите наибольшее значение функции y = ln(11x) – 11x + 9 на отрезке 12. max Наибольшее
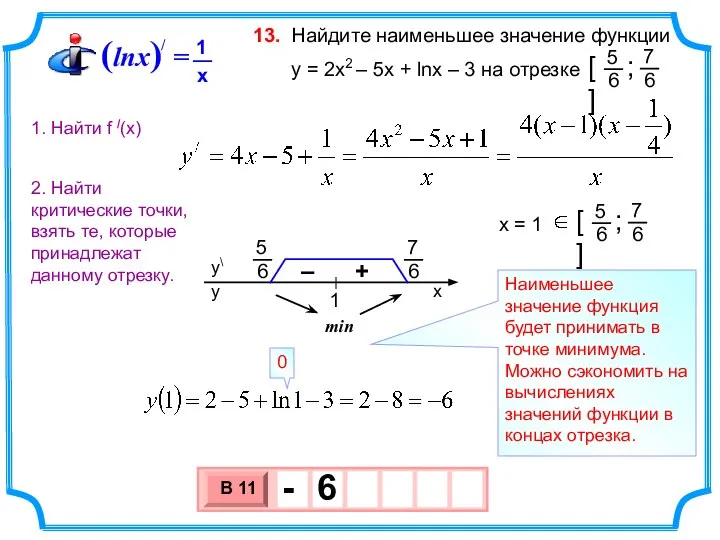
- 20. Найдите наименьшее значение функции y = 2х2 – 5x + lnx – 3 на отрезке 13.
- 21. Найдите наибольшее значение функции y = 7cosx +16x – 2 на отрезке 14. Функция на всей
- 22. Критических точек нет. Тогда наибольшее значение функция будет принимать в одном из концов отрезка. Можно было
- 23. Функция на всей области определения убывает. Нетрудно догадаться, что у / Тогда наименьшее значение функция будет
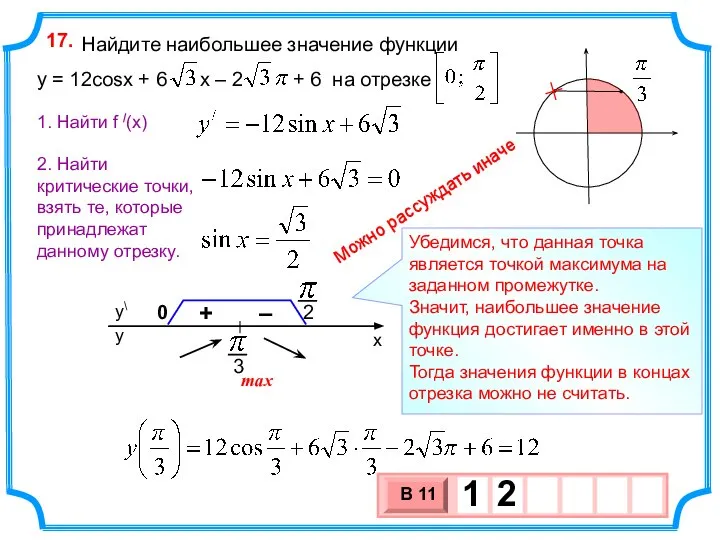
- 24. Найдите наибольшее значение функции y = 12cosx + 6 x – 2 + 6 на отрезке
- 25. Найдите наибольшее значение функции y = 12cosx + 6 x – 2 + 6 на отрезке
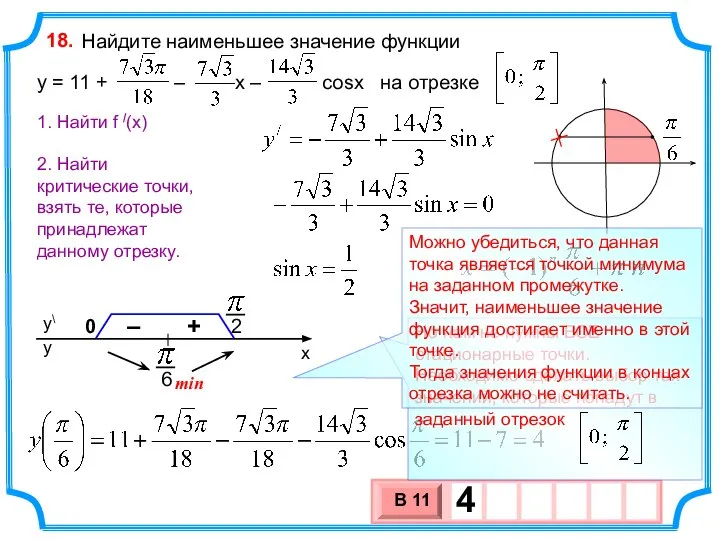
- 26. Найдите наименьшее значение функции y = 11 + – х – cosx на отрезке 18. 1.
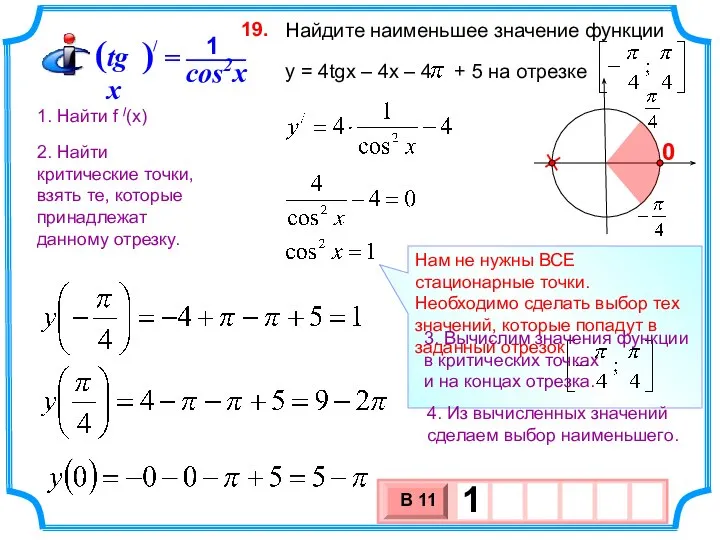
- 27. Найдите наименьшее значение функции y = 4tgx – 4x – 4 + 5 на отрезке 19.
- 29. Скачать презентацию




![Найдите наибольшее значение функции на отрезке [ -3; 3 ] 4. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/966281/slide-9.jpg)
![Найдите наибольшее значение функции на отрезке [ 1; 9 ] 5. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/966281/slide-10.jpg)
![Найдите наименьшее значение функции на отрезке [ 1; 9 ] 6. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/966281/slide-11.jpg)
![Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/966281/slide-12.jpg)
![Найдите наименьшее значение функции на отрезке [-10; 1 ] 7. Найдем критические](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/966281/slide-13.jpg)
![Найдите наибольшее значение функции на отрезке [ 1; 9 ] 8. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/966281/slide-14.jpg)
![Найдите наибольшее значение функции на отрезке [ 3; 10 ] 9. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/966281/slide-15.jpg)
![Найдите наименьшее значение функции на отрезке [ 1; 7 ] 10. Найдем](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/966281/slide-16.jpg)





 Вероятность события. Разбор задач
Вероятность события. Разбор задач Прямоугольники. Противолежащие грани (развертка № 17)
Прямоугольники. Противолежащие грани (развертка № 17) Задачи на разрезание и перекраивание фигур
Задачи на разрезание и перекраивание фигур Презентация на тему Принцип Дирихле
Презентация на тему Принцип Дирихле  Презентация на тему Геометрический смысл модуля действительного числа
Презентация на тему Геометрический смысл модуля действительного числа  Ромашка
Ромашка Михаил Васильевич Ломоносов. Умножение и деление степеней с натуральными показателями
Михаил Васильевич Ломоносов. Умножение и деление степеней с натуральными показателями Статистический анализ данных в пакете Statistica
Статистический анализ данных в пакете Statistica Умножение смешанных дробей
Умножение смешанных дробей Задачи с экономическим содержанием. Часть 1
Задачи с экономическим содержанием. Часть 1 Восстановить цепочку вычислений
Восстановить цепочку вычислений Геометрия треугольника
Геометрия треугольника Презентация Понономарев
Презентация Понономарев Метрология как наука
Метрология как наука Рисуем по координатам
Рисуем по координатам Зачет по теме Параллельность прямых, прямой и плоскости
Зачет по теме Параллельность прямых, прямой и плоскости Многогранники и тела с кривыми поверхностями
Многогранники и тела с кривыми поверхностями Аксиомы стереометрии. Следствия из аксиом
Аксиомы стереометрии. Следствия из аксиом Рисование узора из геометрических фигур
Рисование узора из геометрических фигур Правильный восьмиугольник
Правильный восьмиугольник Многогранники. Тетраэдр
Многогранники. Тетраэдр Измерение углов (5 класс)
Измерение углов (5 класс) Психолого – педагогические основы организации математического развития младших школьников
Психолого – педагогические основы организации математического развития младших школьников Что в центре круга (1 класс)
Что в центре круга (1 класс) Четырехугольники. Геометрический турнир
Четырехугольники. Геометрический турнир Волшебная страна - Геометрия. Занятие 3
Волшебная страна - Геометрия. Занятие 3 угол между прямой и плоскостью (1)
угол между прямой и плоскостью (1) Использование технологии критического мышления учащихся на уроках математики посредством чтения и письма
Использование технологии критического мышления учащихся на уроках математики посредством чтения и письма