Содержание
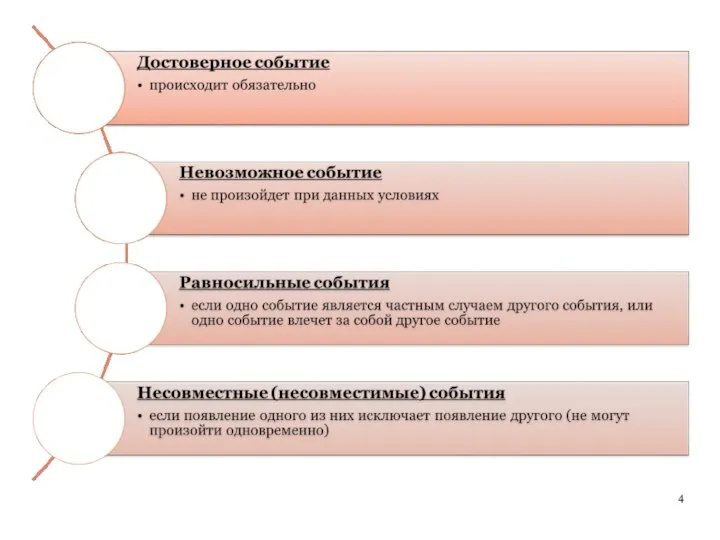
- 2. Теория вероятностей — это математическая наука, изучающая закономерности случайных явлений (событий, величин, функций, процессов и др.).
- 3. Событие (или Случайное событие) — это любой факт, который может либо произойти, либо не произойти при
- 5. Вероятность события - численная мера степени объективной возможности этого события. Вероятность события А обозначается Р(А). Вероятность
- 6. X = xi есть случайное событие, характеризующееся вероятностью P (X = xi) = pi. Случайная величина
- 7. Закон распределения — соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями, с которыми
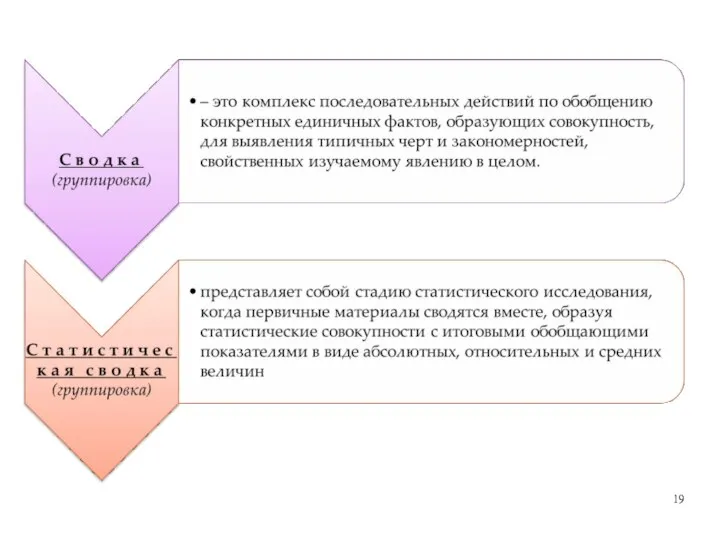
- 9. Математическая статистика — раздел математики, изучающий методы обработки результатов массовых случайных явлений с целью выявления статистических
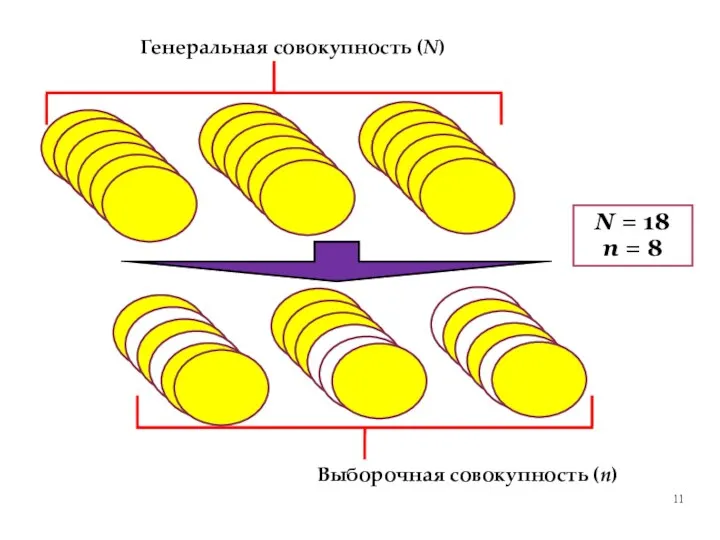
- 11. Генеральная совокупность (N) Выборочная совокупность (n) N = 18 n = 8
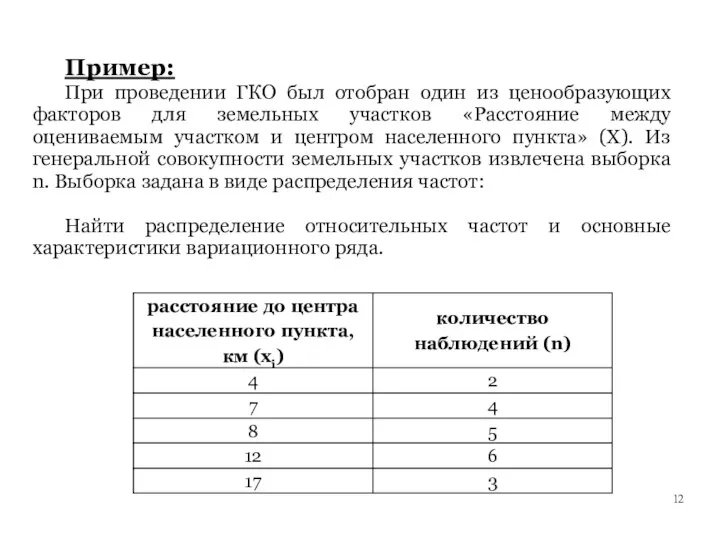
- 12. Пример: При проведении ГКО был отобран один из ценообразующих факторов для земельных участков «Расстояние между оцениваемым
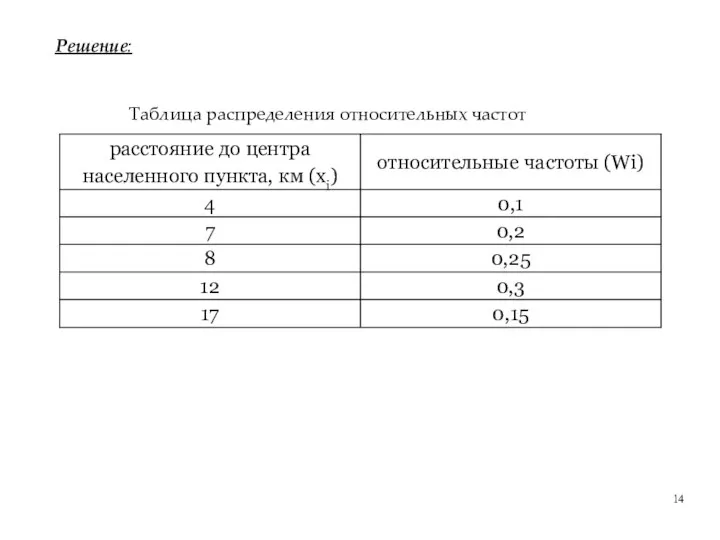
- 14. Решение: Таблица распределения относительных частот
- 15. Решение: Мода (M0 ) - варианта, имеющая наибольшую частоту. M0 = 12 Медиана (me) - варианта,
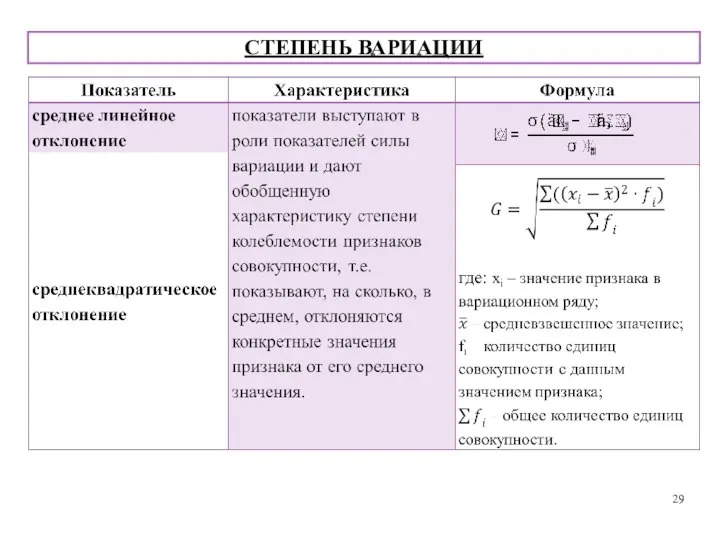
- 16. Дисперсия - это мера разброса значений случайной величины относительно среднего значения случайной величины. Дисперсия показывает, насколько
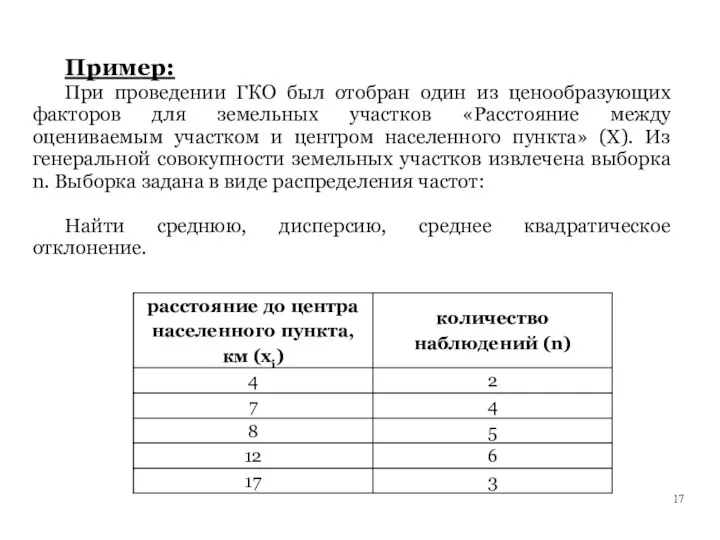
- 17. Пример: При проведении ГКО был отобран один из ценообразующих факторов для земельных участков «Расстояние между оцениваемым
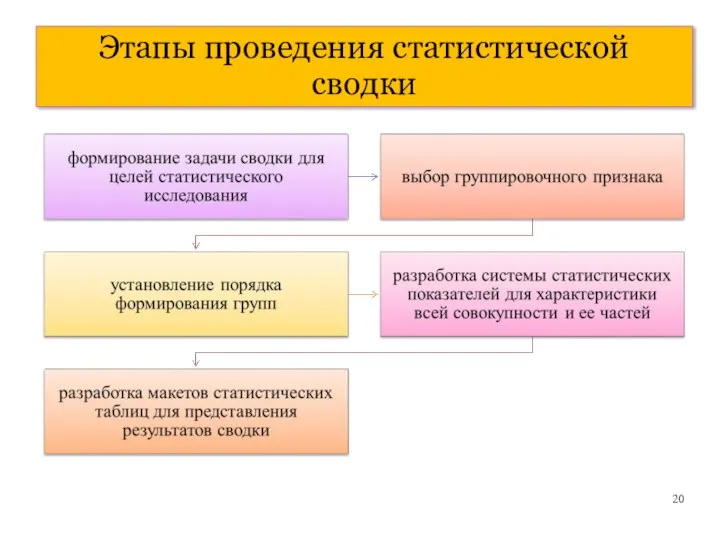
- 20. Этапы проведения статистической сводки
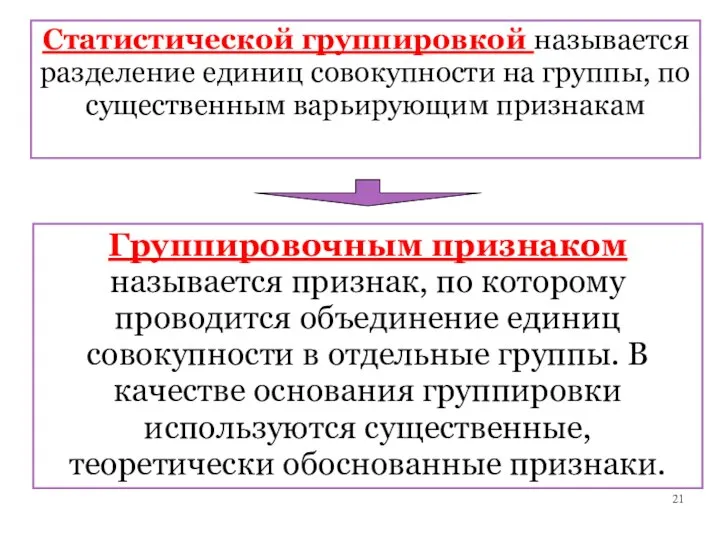
- 21. Статистической группировкой называется разделение единиц совокупности на группы, по существенным варьирующим признакам Группировочным признаком называется признак,
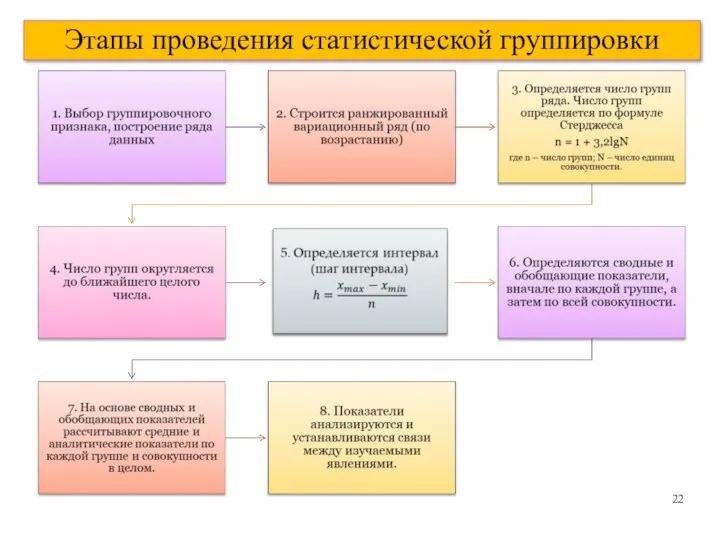
- 22. Этапы проведения статистической группировки
- 23. Для каждого массового процесса, явления, необходимо так же соблюдение определенных условий - «допусков» - т.е. специфическая
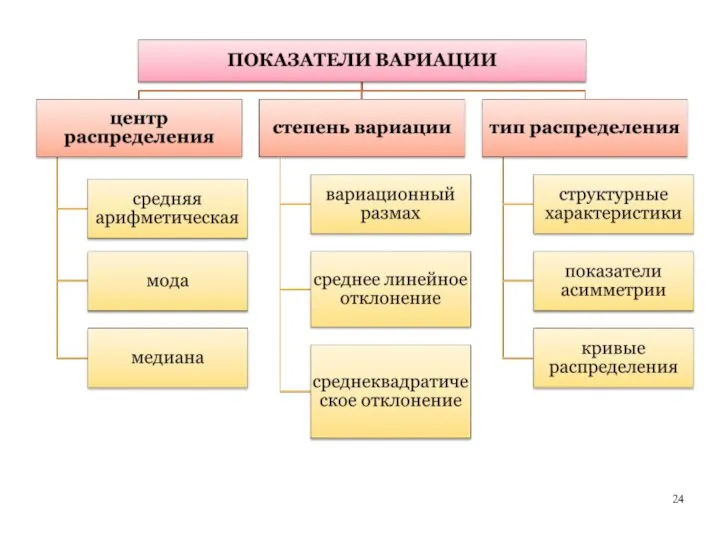
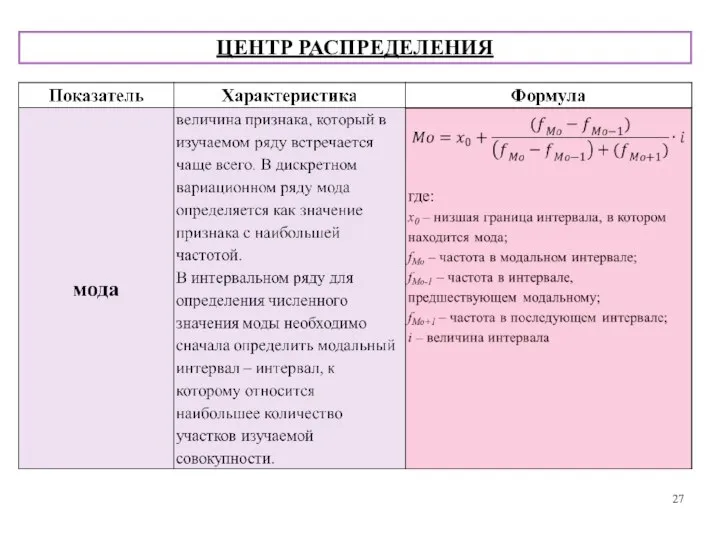
- 25. ЦЕНТР РАСПРЕДЕЛЕНИЯ
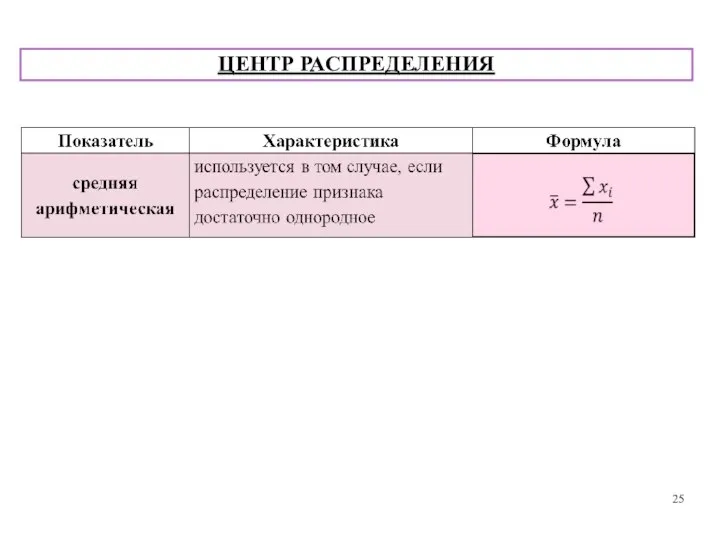
- 26. ЦЕНТР РАСПРЕДЕЛЕНИЯ
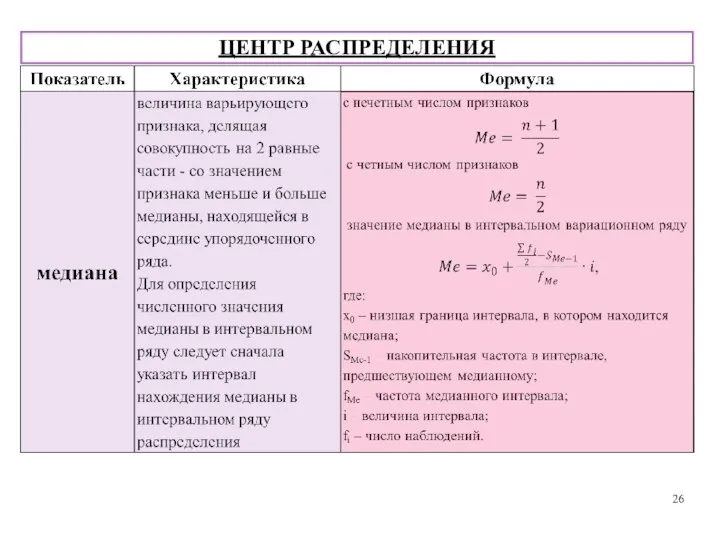
- 27. ЦЕНТР РАСПРЕДЕЛЕНИЯ
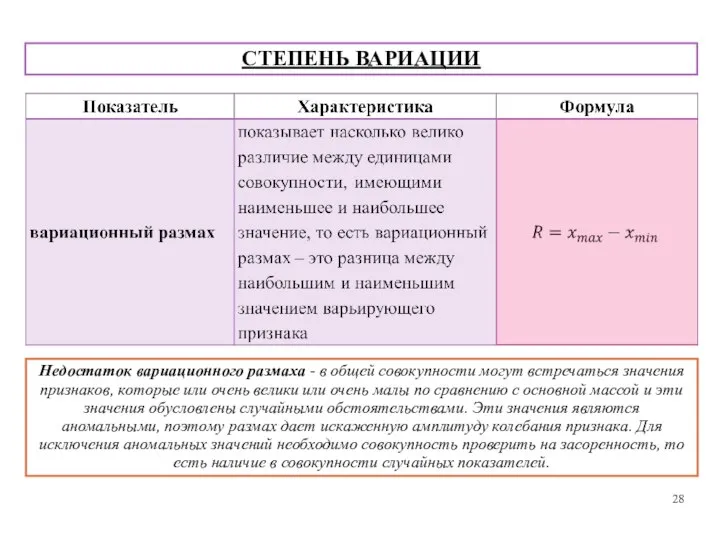
- 28. СТЕПЕНЬ ВАРИАЦИИ Недостаток вариационного размаха - в общей совокупности могут встречаться значения признаков, которые или очень
- 29. СТЕПЕНЬ ВАРИАЦИИ
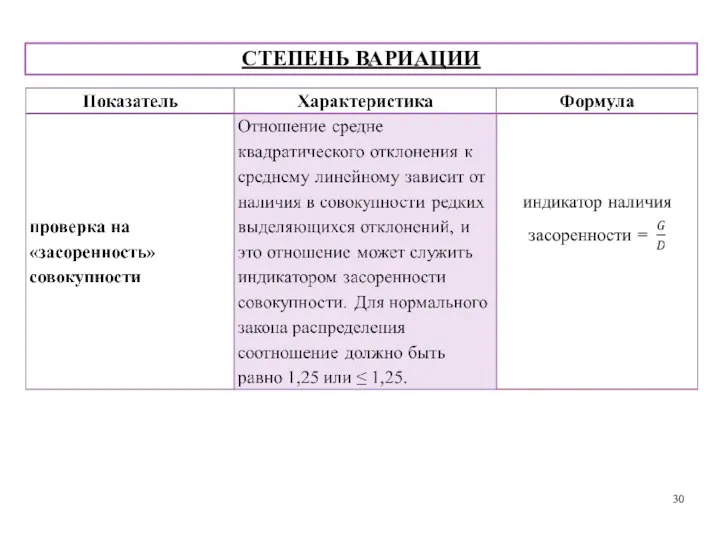
- 30. СТЕПЕНЬ ВАРИАЦИИ
- 31. Если соотношение фиксирует засоренность, необходимо найти признаки, которые засоряют совокупность. Рекомендуется исключить их, снова проверить совокупность,
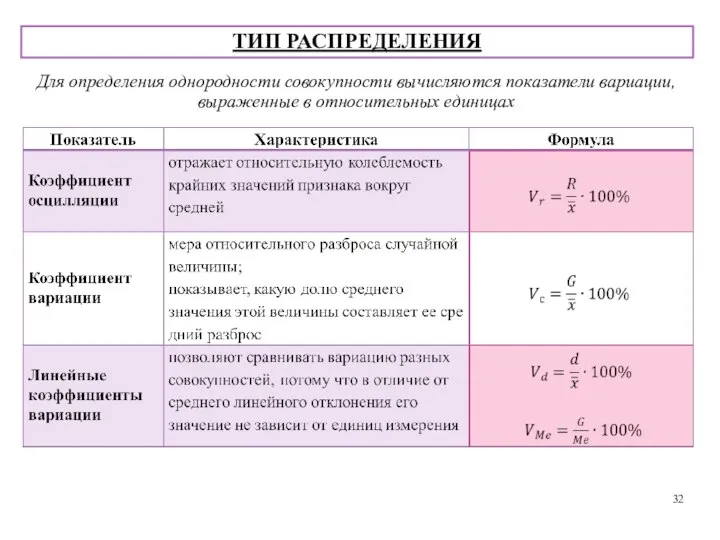
- 32. Для определения однородности совокупности вычисляются показатели вариации, выраженные в относительных единицах ТИП РАСПРЕДЕЛЕНИЯ
- 33. Совокупность считается не засоренной, если выполняются следующие условия: значение медианы находится между средневзвешенной и модой; отношение
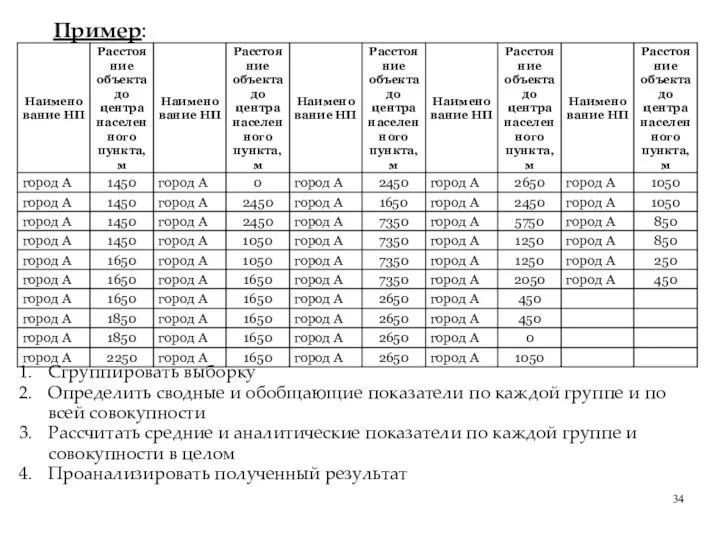
- 34. Пример: Сгруппировать выборку Определить сводные и обобщающие показатели по каждой группе и по всей совокупности Рассчитать
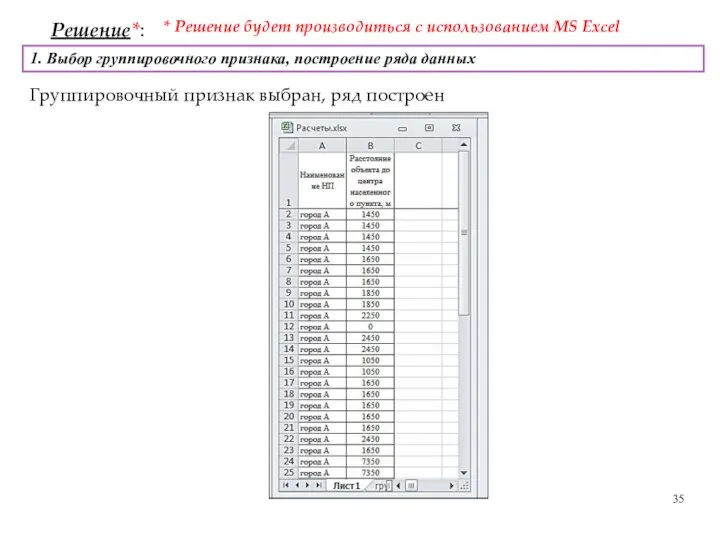
- 35. Решение*: * Решение будет производиться с использованием MS Excel 1. Выбор группировочного признака, построение ряда данных
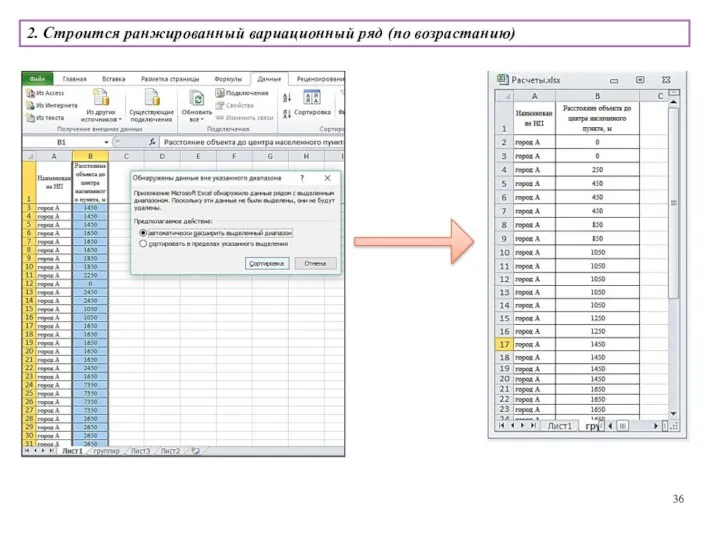
- 36. 2. Строится ранжированный вариационный ряд (по возрастанию)
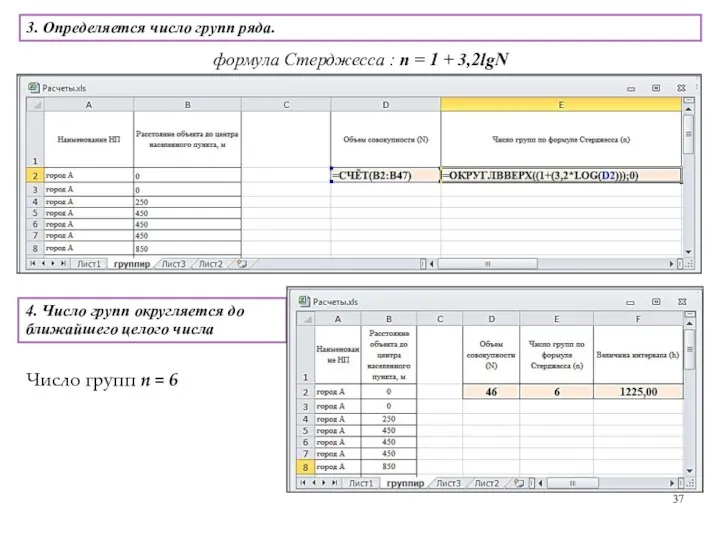
- 37. 3. Определяется число групп ряда. формула Стерджесса : n = 1 + 3,2lgN 4. Число групп
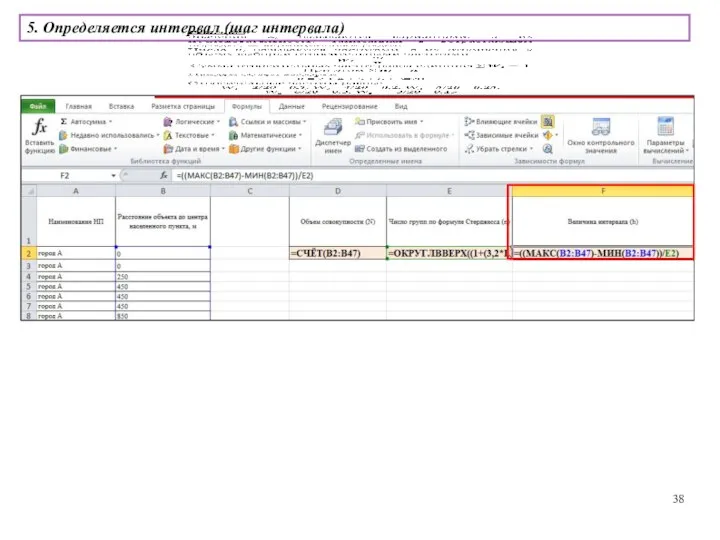
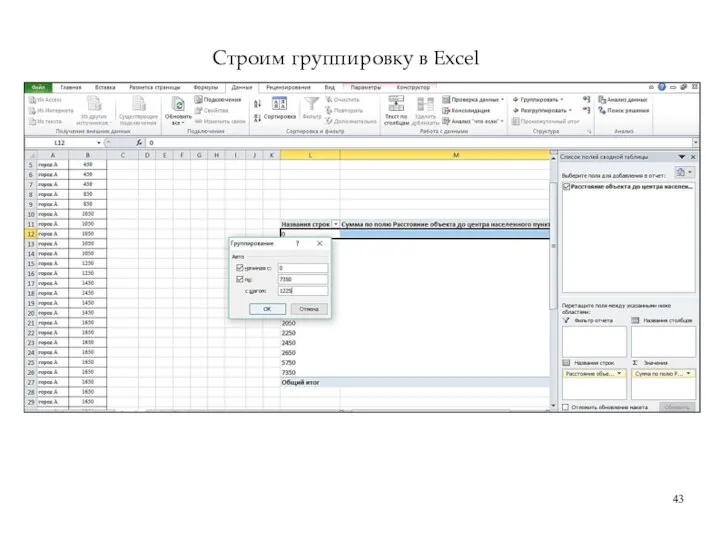
- 38. 5. Определяется интервал (шаг интервала)
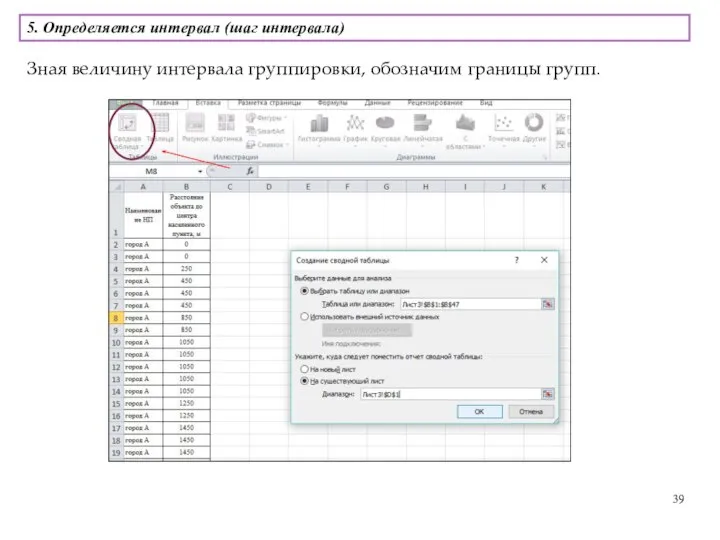
- 39. Зная величину интервала группировки, обозначим границы групп. 5. Определяется интервал (шаг интервала)
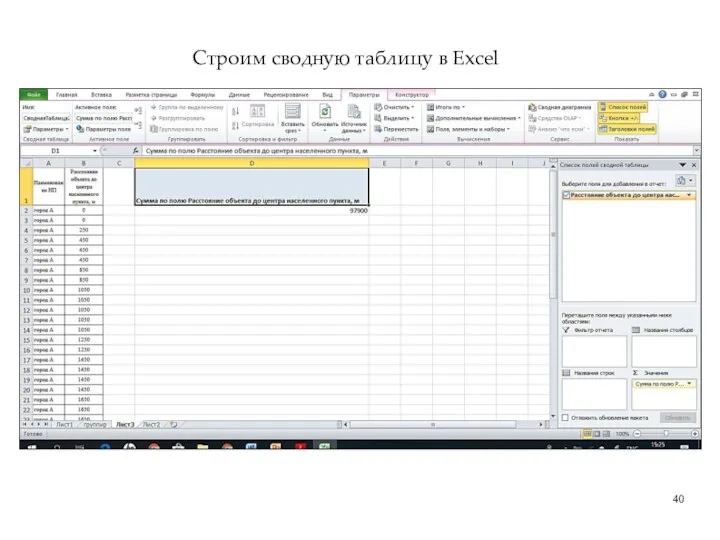
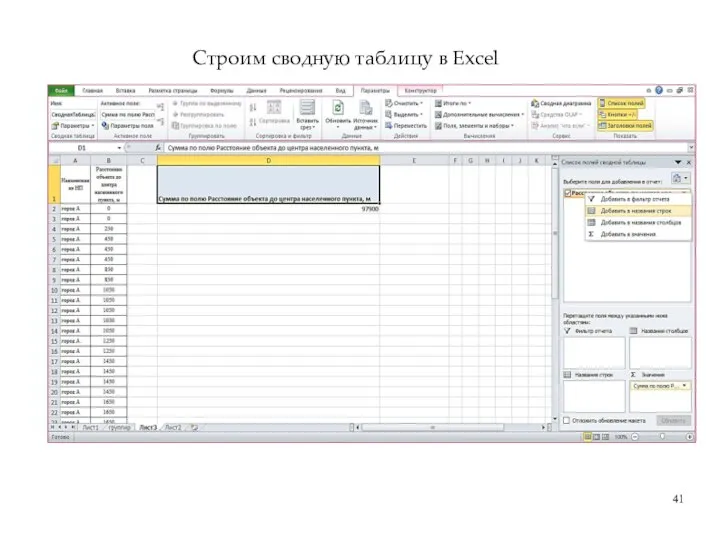
- 40. Строим сводную таблицу в Excel
- 41. Строим сводную таблицу в Excel
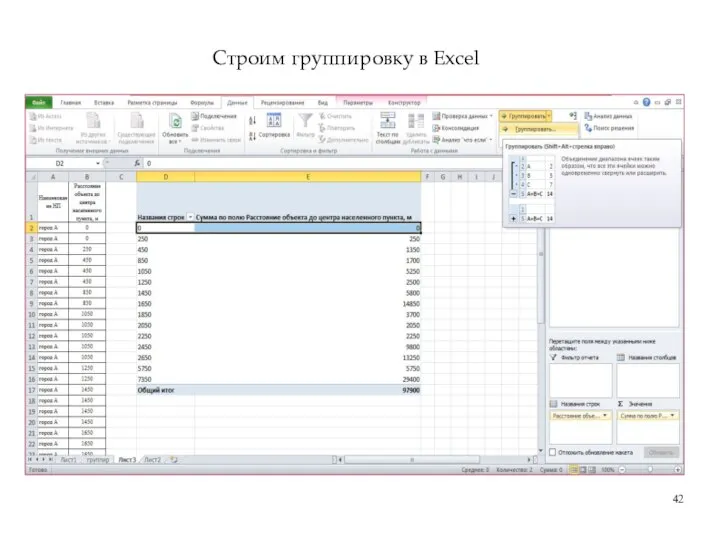
- 42. Строим группировку в Excel
- 43. Строим группировку в Excel
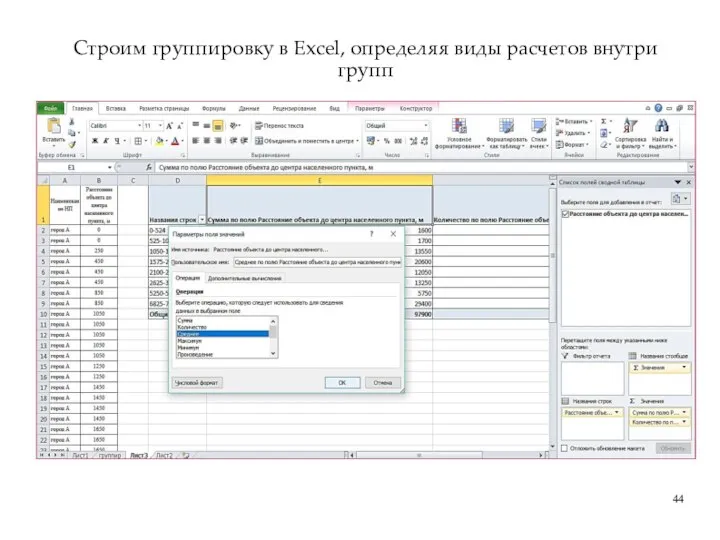
- 44. Строим группировку в Excel, определяя виды расчетов внутри групп
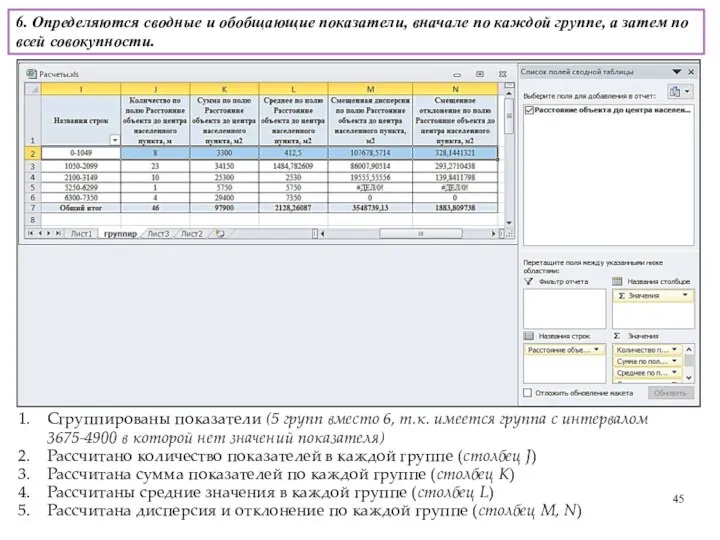
- 45. Сгруппированы показатели (5 групп вместо 6, т.к. имеется группа с интервалом 3675-4900 в которой нет значений
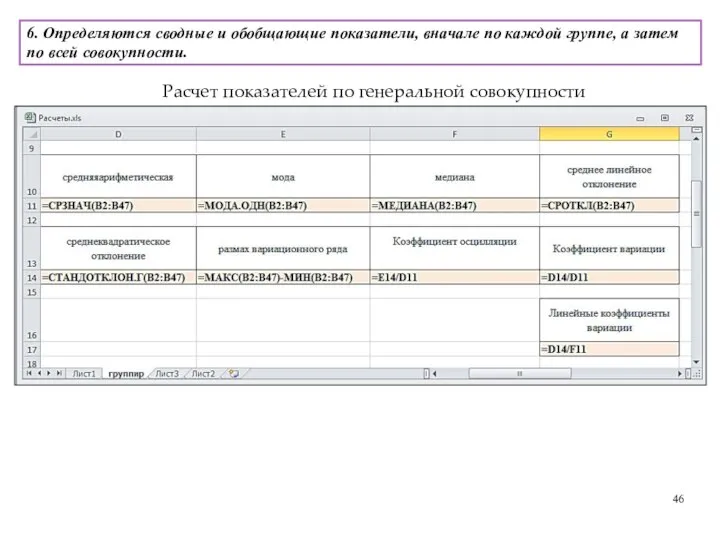
- 46. 6. Определяются сводные и обобщающие показатели, вначале по каждой группе, а затем по всей совокупности. Расчет
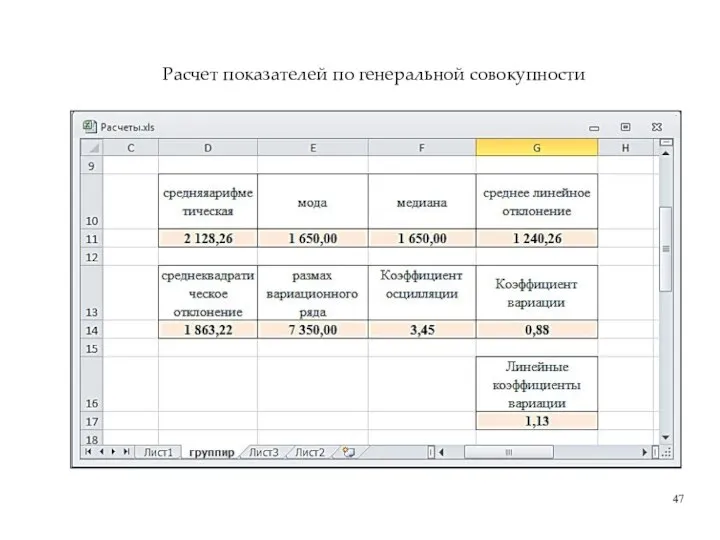
- 47. Расчет показателей по генеральной совокупности
- 48. Должно быть: значение медианы находится между средневзвешенной и модой; отношение среднеквадратического отклонения к среднему линейному отклонению
- 50. Скачать презентацию
















 Построения проекций вершин ребер и граней предмета
Построения проекций вершин ребер и граней предмета тригонометрия 1 урок
тригонометрия 1 урок Презентация на тему Дроби и проценты
Презентация на тему Дроби и проценты  Дидактическая игра Гравити Фолз по математике для учеников 6 класса направленная на итоговое повторение
Дидактическая игра Гравити Фолз по математике для учеников 6 класса направленная на итоговое повторение Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана
Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана Действия в десятичными дробями
Действия в десятичными дробями Неполные квадратные уравнения
Неполные квадратные уравнения Задачи с величинами: цена, количество, стоимость
Задачи с величинами: цена, количество, стоимость Формулы сокращённого умножения
Формулы сокращённого умножения Производная функции. Тест 1
Производная функции. Тест 1 Ментальный счет
Ментальный счет Упрощение выражений. Урок-сказка
Упрощение выражений. Урок-сказка Тест по теме: Объем наклонной призмы, пирамиды и конуса. Вариант 1
Тест по теме: Объем наклонной призмы, пирамиды и конуса. Вариант 1 Решение неравенств
Решение неравенств Алгебра высказываний
Алгебра высказываний Понятие спирали
Понятие спирали Показательные уравнения
Показательные уравнения Функции многих переменных: определение, предел, непрерывность, частные производные. Лекция 1
Функции многих переменных: определение, предел, непрерывность, частные производные. Лекция 1 Среднее арифметическое
Среднее арифметическое Тренажёр по математике 4 класс. Умножение и деление многозначных чисел на однозначное
Тренажёр по математике 4 класс. Умножение и деление многозначных чисел на однозначное Двоичная арифметика
Двоичная арифметика Буквенная запись свойств действий над числами
Буквенная запись свойств действий над числами Арифметическая прогрессия в истории
Арифметическая прогрессия в истории Понятие вектора. Равенство векторов
Понятие вектора. Равенство векторов Линейные пространства и линейные операторы. Лекция 3
Линейные пространства и линейные операторы. Лекция 3 Презентация_по_алгебре_Возрастание_и_убывание_фу
Презентация_по_алгебре_Возрастание_и_убывание_фу Obratnye_trigonometricheskie_funktsii (1)
Obratnye_trigonometricheskie_funktsii (1) Ноль и нуль
Ноль и нуль