Содержание
- 2. Лекция 5
- 3. Вероятности сложных событий
- 4. Теорема сложения Вероятность появления суммы двух несовместных событий Р ( А + В ) = Р
- 5. Вероятность появления суммы нескольких попарно несовместных событий
- 6. Сумма вероятностей противоположных событий равна единице:
- 7. Теорема о сумме любых событий Р (А+В) = Р (А) + Р (В) – Р (АВ)
- 8. NEW: Теорема о сумме любых событий. Р (А+В) = Р (А) + Р (В) – Р
- 9. Доказательство.
- 10. По теореме сложения вероятностей
- 11. Условная вероятность
- 12. Пример Студент выучил 20 из 25 экзаменационных вопросов. Найти вероятность того, что студент ответит на предложенные
- 13. Решение Обозначим события A={студент ответит на первый вопрос} B={студент ответит на второй вопрос} C={студент ответит на
- 14. Тогда искомая вероятность P(ABC)=20/25·19/24·18/23=0,496
- 15. Теорема умножения вероятностей
- 16. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести
- 17. Учитывая lg0.6
- 18. Формула полной вероятности Пусть событие А может наступить при условии появления одного из несовместных событий которые
- 19. Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий образующих
- 20. Пример Имеется два набора деталей. Вероятность того, что деталь первого набора стандартна, равна 0,8, а второго
- 21. Решение А= {«извлечённая деталь стандартна»}. Деталь из первого набора ( ), либо второго ( ).
- 23. Пример . В первой коробке содержится 20 радиоламп, из них 18 стандартных; во второй коробке –
- 24. Решение А ={из первой коробки извлечена стандартная лампа}. Из второй коробки могла быть извлечена либо стандартная
- 27. Вероятность гипотез Формула Байеса Пусть событие А может наступить при условии появления одного из несовместных событий
- 28. Допустим, что произведено испытание, в результате которого появилось событие А.
- 29. Будем искать условные вероятности
- 31. Заменив здесь P(A) , получим
- 33. Полученные формулы называют формулами Байеса (по имени английского математика, который их вывел; опубликованы в 1764г.).
- 34. Формулы Бейеса позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого
- 35. Пример. Детали, изготовленные цехом завода, попадают для проверки их на стандартность к одному из двух контролёров.
- 36. Вероятность того, что годная деталь будет признана стандартной первым контролёром, равна 0,94, а вторым – 0,98.
- 37. Решение А={ деталь признана стандартной}. Два предположения: B1={деталь проверил первый контролёр} ; B2={деталь проверил второй контролёр}
- 39. Задача Есть 50 белых и 50 черных шаров. Их разложили в два ящика: в первый положили
- 42. Задачи
- 43. Задача 1 В первом ящике имеется 20 деталей, из них 15 стандартных, во втором – 30,
- 44. Решение Обозначим A={вынута стандартная деталь} B1={стандартная деталь из ящика 1} B2={стандартная деталь из ящика 2} B3={стандартная
- 45. Условные вероятности
- 46. По формуле полной вероятности
- 47. Задача 2 Имеется 5 винтовок: 3 с оптическим прицелом, 2 без оптического прицела. Вероятность поразить мишень
- 48. Решение A={цель поражена} B1={взята винтовка с оптич. прицелом} B2={взята винтовка без оптического прицела} Найдем вероятности P(B1)=3/5
- 49. Условные вероятности Тогда искомая вероятность
- 50. Задача 3 В продажу поступили телевизоры трех заводов. Продукция первого завода содержит 10% телевизоров с дефектов,
- 51. Решение A={приобретенный телевизор с дефектом} B1={телевизор выпущен первым заводом} B2={телевизор выпущен вторым заводом} B3={телевизор выпущен третьим
- 52. Вероятности P(B1)=0,25; P(B2)=0,55; P(B3)=0,20 Условные вероятности P(A|B1)=0,1 P(A|B2)=0,05 P(A|B3)=0,03 По формуле полной вероятности P(A)=0,25·0,1+0,55·0,05+0,20·0,03= =0,0585
- 53. Задача 4 В группе студентов 12 юношей и 8 девушек. Зачет по ТВ и МС сдает,
- 54. Решение A={сдал зачет по ТВ И МС} B1={первый вышел юноша} B2={первой вышла девушка} Вероятности P(B1)=12/20; P(B2)=8/20
- 55. Условные вероятности P(A|B1)=0,70 – вероятность сдать зачет, при условии, что вышел юноша P(A|B2)=0,80 – вероятность сдать
- 56. Задача 5 В группе спортсменов 20 лыжников, 6 велосипедистов, 4 бегуна. Вероятность выполнить квал. норму для
- 57. Решение A={спортсмен выполнит норму} B1={выбран лыжник} B2={выбран велосипедист} B3={выбран бегун} Вероятности P(B1)=20/30; P(B2)=6/30; P(B3)=4/30
- 58. Условные вероятности P(A|B1)=0,9; P(A|B2)=0,8; P(A|B3)=0,75 По формуле полной вероятности P(A)=20/30·0,9+6/30·0,8+4/30·0,75
- 59. Задача 6 В торговую фирму поступили телевизоры от трех поставщиков в отношении 1:4:5. Телевизоры от первого
- 60. Решение A={телевизор не потребует ремонта в гарантийный срок} B1={телевизор от поставщика 1} B2={телевизор от поставщика 2}
- 61. Условные вероятности P(A|B1)=0,98; P(A|B2)=0,88; P(A|B3)=0,92 По формуле полной вероятности P(A)=0,1·0,98+0,4·0,88+0,5·0,92
- 62. Задача 7 Вероятности сбоя для различных элементов в компьютере относятся как 3:2:5. Вероятности обнаружения сбоя в
- 63. Решение A={сбой будет обнаружен} B1={сбой в устройстве 1} B2={сбой в устройстве 2} B3={сбой в устройстве 3}
- 64. Условные вероятности P(A|B1)=0,8; P(A|B2)=0,9; P(A|B3)=0,9 По формуле полной вероятности P(A)=0,3·0,8+0,2·0,9+0,5·0,9=0,87
- 65. Задача 8 У рыбака есть три любимых места рыбалка. Эти места он посещает с одинаковой вероятностью.
- 66. Решение A={рыбак вытащил рыбку} B1={рыбачил в первом месте} B2={рыбачил во втором месте} B3={рыбачил в третьем месте}
- 67. Условные вероятности P(A|B1)=1/3; P(A|B2)=1/2; P(A|B3)=1/4 По формуле Байеса
- 68. Задача 9 Путешественник может купить билет в одной из трех касс ж/д вокзала. Вероятность, что он
- 69. Решение A={купил билет} B1={обратился в кассу 1} B2={обратился в кассу 2} B3={обратился в кассу 3} Вероятности
- 70. Так как в условии задачи даны вероятности, что билетов в кассах уже нет, а путешественник купил
- 71. Искомая вероятность
- 72. Задача 10 Турист, заблудившись в лесу, вышел на полянку, от которой в разные стороны ведут 5
- 73. Решение A={турист вышел из леса} B1={выбрал дорогу 1} B2={выбрал дорогу 2} B3={выбрал дорогу 3} B4={выбрал дорогу
- 74. Дорог всего 5. Вероятности пойти по любой из пяти дорог одинаковы, то есть P(B1)=P(B2)=P(B3)=P(B4)=P(B5)=1/5 Условные вероятности
- 75. Имеем
- 76. Вопросы к лекции 5 Теорема сложения для любых событий Условная вероятность Формула полной вероятности Формула Байеса
- 78. Скачать презентацию







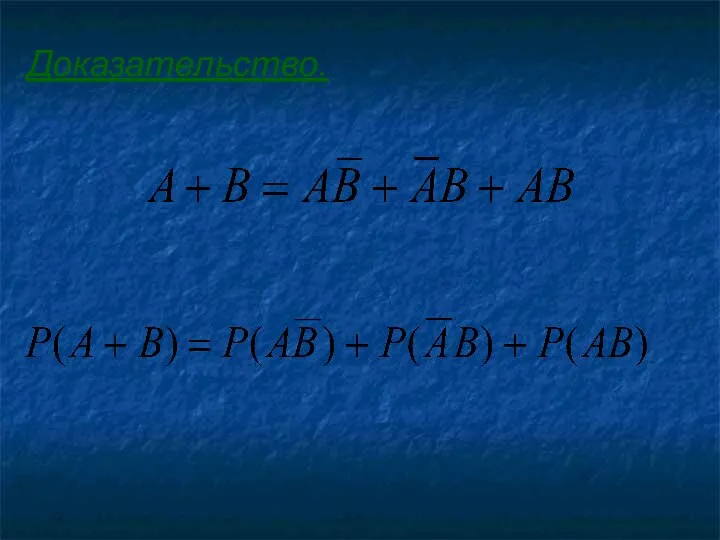












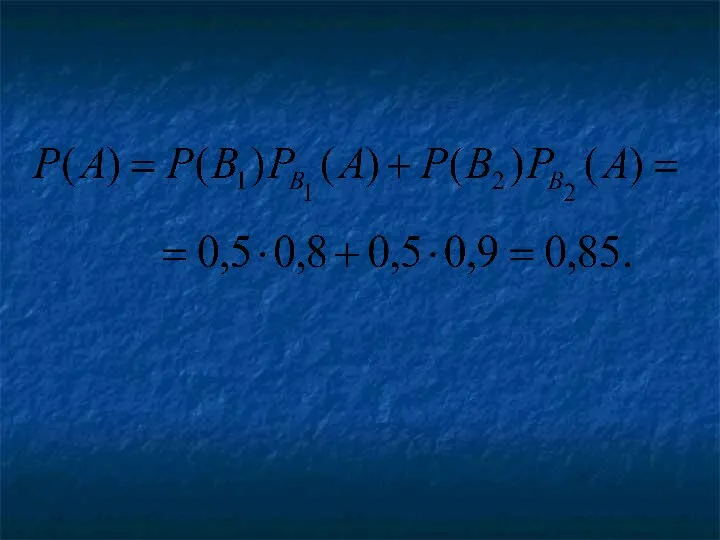


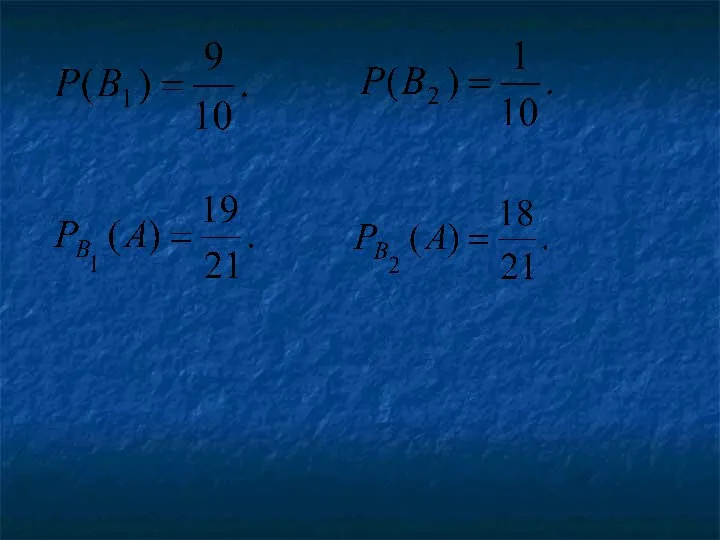
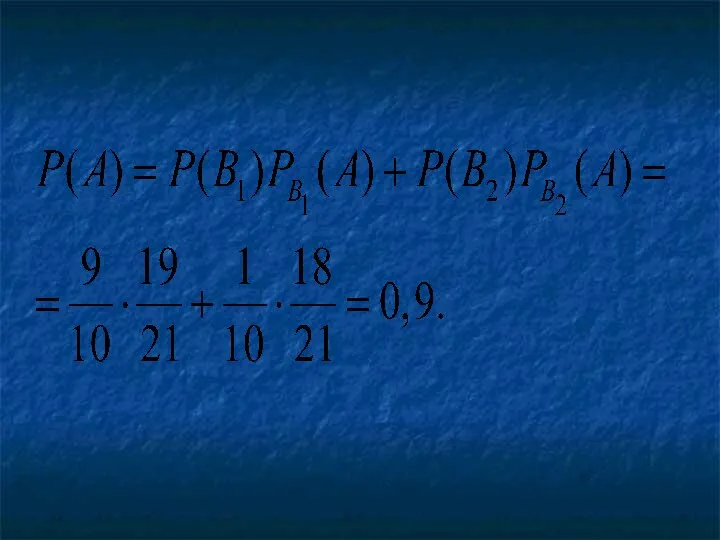



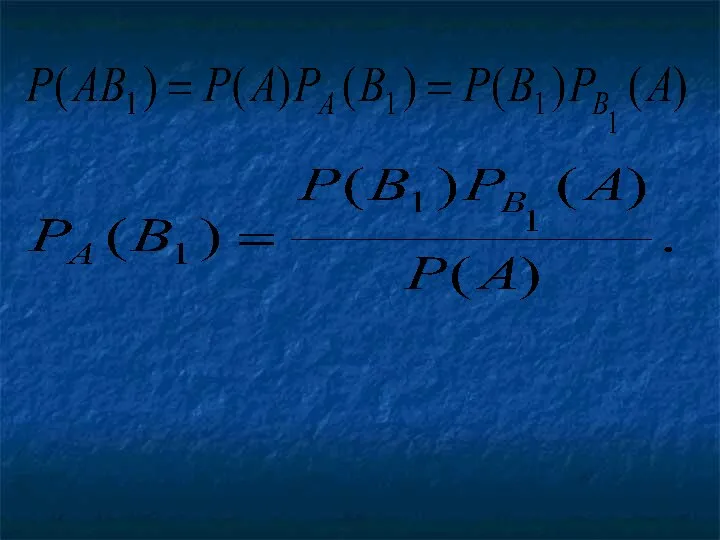

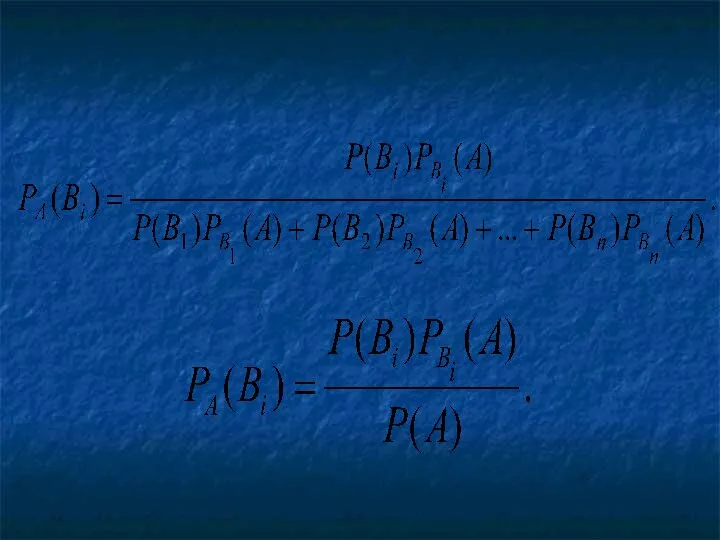





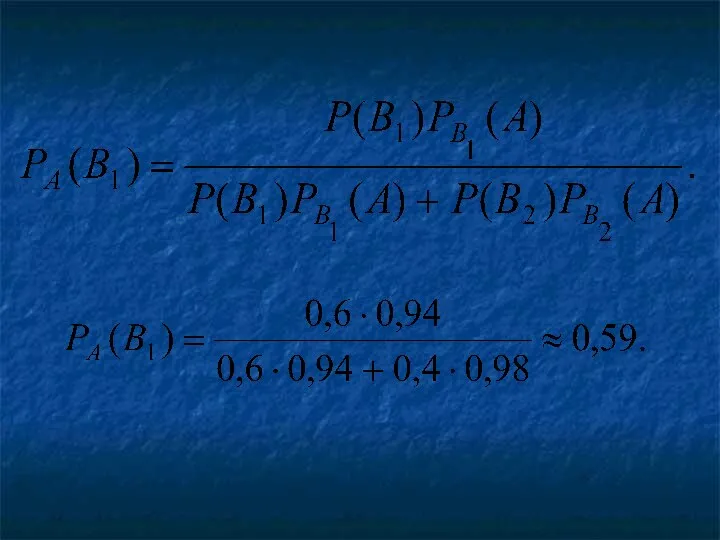


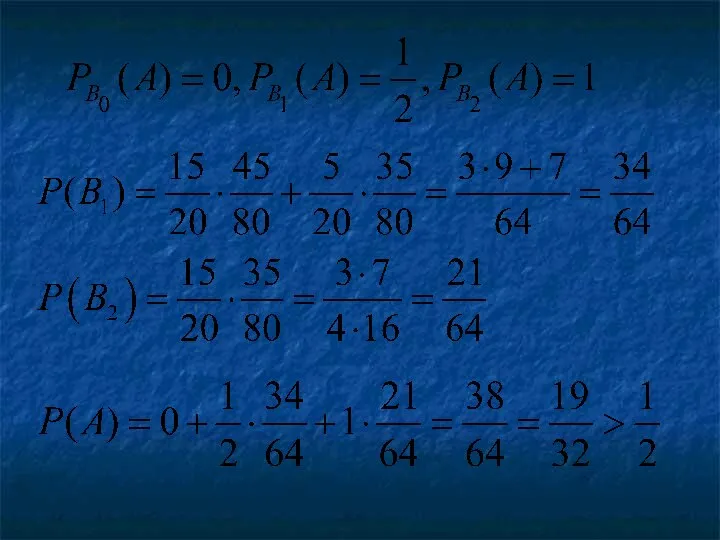





























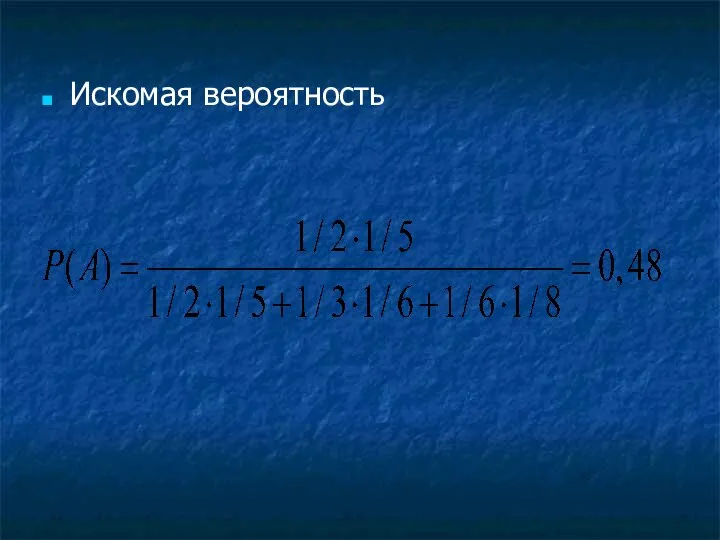





 Эконометрика. Лекция 2
Эконометрика. Лекция 2 Метод координат в пространстве
Метод координат в пространстве Треугольник. Повторение. Задачи на проверку истинности утверждений
Треугольник. Повторение. Задачи на проверку истинности утверждений Задачки со всего света. Проект Секреты чисел. Команда Искорка
Задачки со всего света. Проект Секреты чисел. Команда Искорка Числовi послiдовностi. Властивостi числових послiдовностей
Числовi послiдовностi. Властивостi числових послiдовностей Презентация на тему Геометрические преобразования в пространстве
Презентация на тему Геометрические преобразования в пространстве  Презентация на тему Умножение и деление многозначного числа на однозначное
Презентация на тему Умножение и деление многозначного числа на однозначное  Методика ознакомления обучающихся с геометрическими фигурами (прямой, ломаной) и их свойствами
Методика ознакомления обучающихся с геометрическими фигурами (прямой, ломаной) и их свойствами Иррациональные уравнения
Иррациональные уравнения Корреляционный анализ. (Тема 3)
Корреляционный анализ. (Тема 3) Треугольник
Треугольник Элементы комбинаторики
Элементы комбинаторики Многогранники: выпуклые призмы и антипризмы
Многогранники: выпуклые призмы и антипризмы Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Устный счёт. Деление на двузначное число
Устный счёт. Деление на двузначное число Презентация на тему Умножение двузначного числа на однозначное (3 класс)
Презентация на тему Умножение двузначного числа на однозначное (3 класс)  Это полезно знать. Интересные факты из жизни самых больших чисел
Это полезно знать. Интересные факты из жизни самых больших чисел Векторы в пространстве
Векторы в пространстве Математика. Основные понятия математики
Математика. Основные понятия математики Презентация на тему Преобразование плоскости
Презентация на тему Преобразование плоскости  Проценты
Проценты Морфизмы алгебр
Морфизмы алгебр Сфера и шар
Сфера и шар Сколько останется? Посчитай и назови ответ
Сколько останется? Посчитай и назови ответ Графіка. Лінійна перспектива. Графічне зображення ,,Куб
Графіка. Лінійна перспектива. Графічне зображення ,,Куб Замена числа суммой разрядных слагаемых. (дистанционное обучение)
Замена числа суммой разрядных слагаемых. (дистанционное обучение) Диагонали треугольника равны
Диагонали треугольника равны Розв'язування типових задач
Розв'язування типових задач