Прикладная физика кровообращения

Кровообращение как система
Все вокруг нас – системы
Система :
комплекс элементов,
которые связаны друг с другом
и взаимодействуют между собой определенным образом
для выполнения определенной цели

Цель системы кровообращения
Основная цель – обеспечение транспорта питательных веществ к тканям
Питательные вещества – глюкоза, вода, аминокислоты, жирные кислоты, кислород
КИСЛОРОД – вещество, запасов которого в крови хватает на 5 мин жизнедеятельности
ОСНОВНАЯ ЦЕЛЬ СИСТЕМЫ КРОВООБРАЩЕНИЯ – ТРАНСПОРТ КИСЛОРОДА К ТКАНЯМ

Транспорт кислорода
DO2 = МОК х (1,34 х Нв х SaO2)
доставка выброс содержание О2
DO2 = МОК х (1,34 х 140 х 0,98) = МОК х 184мл/л
МОК в норме – 0,1 л/кг/мин или 3,9 л/м2/мин
При МОК = 7 л/мин DO2 = 1288 мл/мин или 718мл/м2/мин

Потребление кислорода
VO2 = МОК х 1,34 x Hb x (SaO2 – SvO2)
При SaO2=0,98 и SvO2=0,73
VO2 = МОК х 1,34 x 140 x (0,98 – 0,73) = МОК х 47 мл/л
При МОК = 7 л/мин VO2 = 329 мл/мин или 183 мл/м2/мин
Коэффициент экстракции О2 = 0,25 (0,2-0,3) – используется только 25% всего приносимого к тканям кислорода

Потребность тканей может увеличиться в 20 – 30 раз
Максимальный коэффициент экстракции – 50-60%, т.е. – экстракция может увеличиться лишь в 2-3раза
Сердечный выброс может увеличиться лишь в 5–7 раз (в покое – 5 л/мин)
Третий вариант обеспечения потребности – перераспределение кровотока

Закон Ома
Сила тока = Напряжение / Сопротивление
МОК = АД / ОПСС

Георг Симон Ом (1789 - 1854)
Выдающийся немецкий физик. Изучал электрические явления и акустику. Первоначально публиковал свои открытия в газетах, за что и был уволен министром образования с должности школьного учителя.
С 1849 г. – профессор Мюнхенского университета.

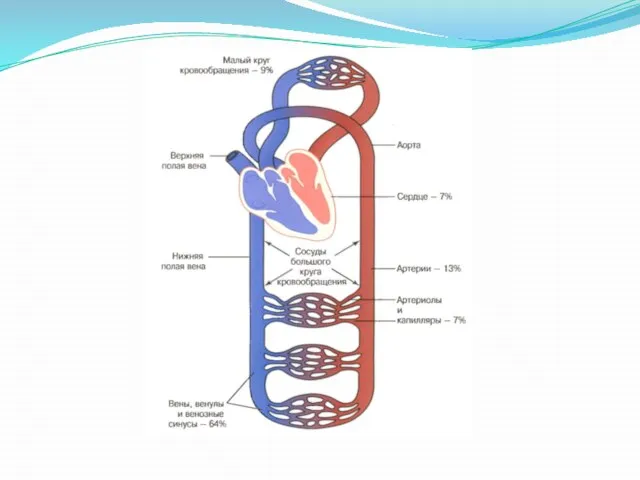
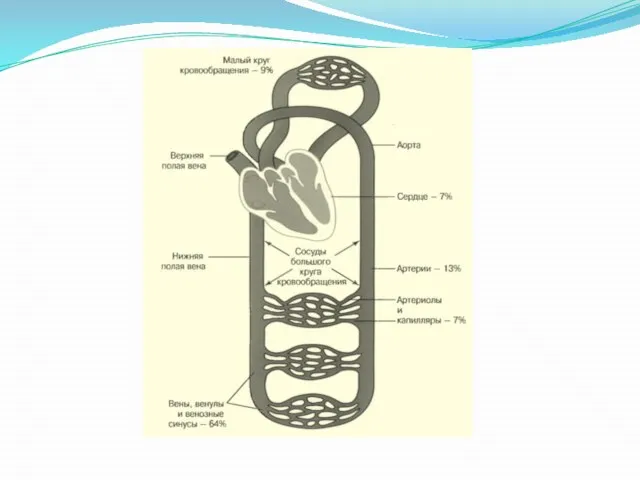
Параллельно и последовательно
Последовательная цепь:
МОК во всех участках цепи одинаков (І=const)
Давление падает (U=U1+U2+U3+…)
Сопротивление складывается (R=R1+R2+R3+…)
Параллельная цепь:
МОК складывается (І=І1+І2+І3+…)
Давление постоянно (U=const)
Складывается проводимость (1/R=1/R1+1/R2+1/R3+…)

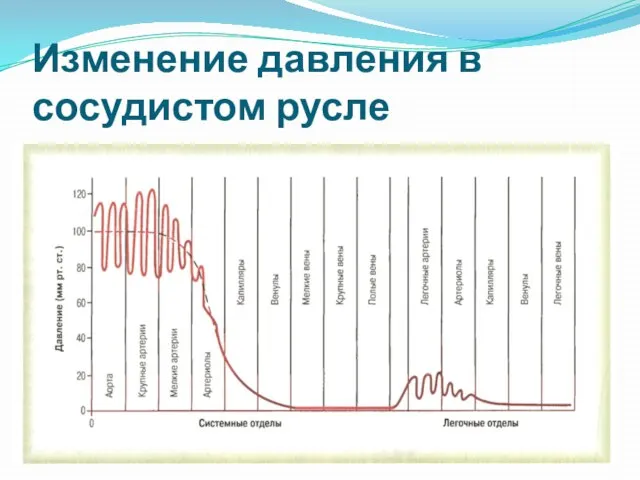
Изменение давления в сосудистом русле

Среднее давление в аорте = 100 торр
Среднее давление в капилляре БКК = 17 торр (35 торр на артериальном конце и 10 торр на венозном)
Среднее давление в месте впадения ВПВ в предсердие = 0 торр
Среднее давление в легочной артерии = 16 торр
Среднее давление в легочных капиллярах = 7 торр

Физика потока
Объемная скорость потока = Разность давлений Сопротивление
Уравнение Хагена – Пуазейля:
Q = ΔP x πR4 / 8Lµ
Вязкость (µ):
прямо пропорциональна Нt
обратно пропорциональна линейной скорости кровотока (принцип кетчупа)

Немецкий физик и гидростроитель, почетный гражданин г. Балтийск
Жан Мари Луи Пуазейль – физик и врач. Первый использовал ртутный тонометр для измерения АД

Физика потока
Объемная скорость = Объем / время (мл/с).
Теоретически – должен соблюдаться принцип постоянной объемной скорости потока!!!
Объемная скорость = Линейная скорость х Площадь,
т.е. – при сужении сосуда линейная скорость растет и наоборот (принцип водохранилища) – венозное депо
Скорость кровотока в аорте = 330 мм/с
Скорость кровотока в капилляре = 0,3 мм/с
Длина капилляра около 0,3 мм, время прохождения кровью капилляра около 1 с

Изменение диаметра сосудистого русла

Реальность потока
Скорость кровотока неодинакова в поперечном сечении сосуда (силы натяжения у стенки)
Постоянна скорость осевого потока
Выброс правого и левого желудочка неодинаков:
Левый желудочек имеет дополнительный легочной «кружок» кровообращения – из бронхиальных артерий в бронхиальные вены

Физика потока
Упрощенное уравнение Бернулли:
Р + ρv2/2 = const,
где Р – давление в потоке
ρ – плотность жидкости
v – линейная скорость потока
При ускорении потока давление снижается и наоборот (принцип инжектора) – обкрадывание коронарных артерий при аортальном стенозе

Даниил Бернулли
Голландский физик, математик, врач. Один из основателей гидродинамики.
Вместе с братом Николаем и другом Леонардом Эйлером работал в Санкт-Петербурге с 1725 по 1733 гг. Почетный член Петербургской Академии.
Ректор Базельского университета.

Поток в артериях и венах
Поток в артериях
Поток в венах
пульсирующий
под высоким давлением
при повышении тонуса артерий кровоток снижается (рост сопротивления)
постоянный
под низким давлением
при повышении тонуса вен (вены не пережимаются!) кровоток растет (выход из депо)

Поток в капиллярах
Поток в капиллярах – всегда пассивен, т.к. капилляры не имеют мышечной стенки.
Приток в капилляры – снижение тонуса артериол
Отток из капилляров – повышение тонуса вен (эффект инжектора = эффект Вентури)
Диаметр эритроцита ~ диаметр капилляра (может пройти только за счет активной деформации!)

Джованни Баттиста Вентури
Современник Леонарда Эйлера и Даниила Бернулли. Итальянский физик. Профессор физики Моденского университета

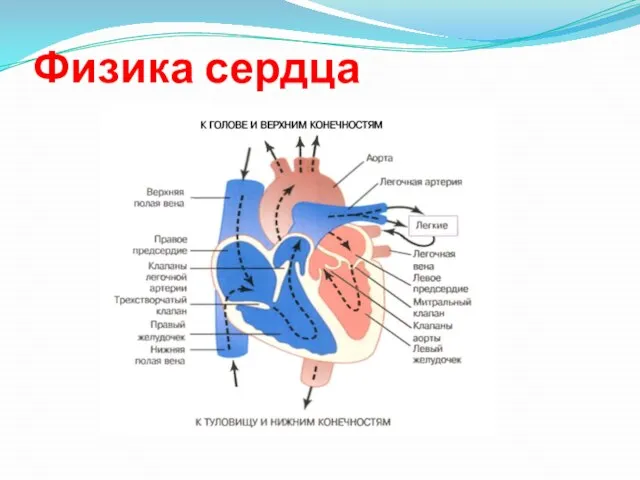
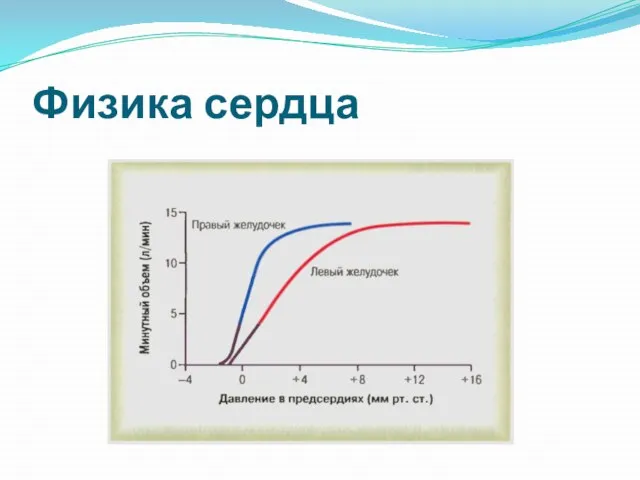
Физика сердца

Физика сердца
Основной показатель работы сердца – сердечный выброс (ударный объем х частота сердечных сокращений)
УО определяется тремя составляющими:
Преднагрузка
Сократимость
Постнагрузка

Физика сердца
Основной закон сердца – закон Франка-Старлинга: чем больше растянута мышца, тем сильнее она сокращается (преднагрузка)
Чем больше приток крови в желудочек, тем больше ударный объем (до определенного момента)

Отто Франк (1865 - 1944) – немецкий врач и физиолог, работал в Мюнхенском университете до 1934 г.
Эрнест генри Старлинг (1866 - 1927) – английский врач и физиолог, профессор Лондонского университета . Автор теории капиллярной фильтрации и термина «гормон»

Физика сердца

Физика сердца
Постнагрузка – работа, которую нужно проделать желудочку для выброса крови
Определяется законом Лапласа:
T = P x R / 2 x H,
где T – напряжение стенки желудочка (постнагрузка), P – трансмуральное давление на стенке, R – радиус полости, Н – толщина стенки

Пьер-Симон Лаплас
Выдающийся математик, физик, астроном. Один из создателей системы дифференциального исчисления и теории вероятностей.
Выходец из крестьян.
Никогда не вступал в конфликт с властями. Член Парижской Академии Наук с 1785 г. Занимал высокие научные посты во времена Французской революции, империи Наполеона Бонапарта, реставрированной династии Бурбонов. Почетный член Петербургской Академии.

Физика сердца
Трансмуральное давление – суммарное давление на стенку желудочка.
Компоненты:
Давление в полости желудочка
Наружное (внутригрудное) давление

Физика сердца
Правый желудочек:
Тонкая стенка (5мм)
Работа против малого давления (Рла = 16 торр)
Высокая зависимость УО от преднагрузки
Левый желудочек:
Толстая стенка (10 мм )
Работа против высокого давления (Рао = 100 торр)
Высокая зависимость УО от сократимости

Коронарный кровоток
Закон Хагена-Пуазейля:
Q = ΔP x π R4 / 8Lµ
Давление!
Радиус сосудов!
Толщина стенки желудочки! (длина)
Вязкость (гематокрит)!
Потребность!!! (постнагрузка, преднагрузка, сократимость и ЧСС)

Коронарный кровоток
Левый желудочек
Толстая стенка – сильное сжатие коронаров в систолу -кровоток в диастолу
Правый желудочек
Тонкая стенка – слабое сжатие коронаров в систолу- кровоток и в систолу, и в диастолу