Содержание
- 2. Что означает владение математикой? Это есть умение решать задачи, причем не только стандартные, но и требующие
- 3. Учебные исследования можно разделить на три вида: монопредметные, межпредметные, надпредметные. Монопредметное исследование — это исследование, выполняемое
- 4. В процессе обучения математике на уроке и во внеклассной работе используется монопредметное исследование. Вместе с тем
- 5. Покажу на примере, как учащиеся вовлекаются в исследовательскую деятельность. Задача Древнегреческих, а также древнеиндийских математиков интересовали
- 6. Фигурные числа
- 7. СОДЕРЖАНИЕ 1.История вопроса. 2.Определение фигурных чисел. 3.Формулы фигурных чисел. 4. Фигурные числа в пространстве.
- 8. Опунтиус Эратосфен Диофант
- 9. Треугольные числа 1,3,6,10,15,21,28,36,45….
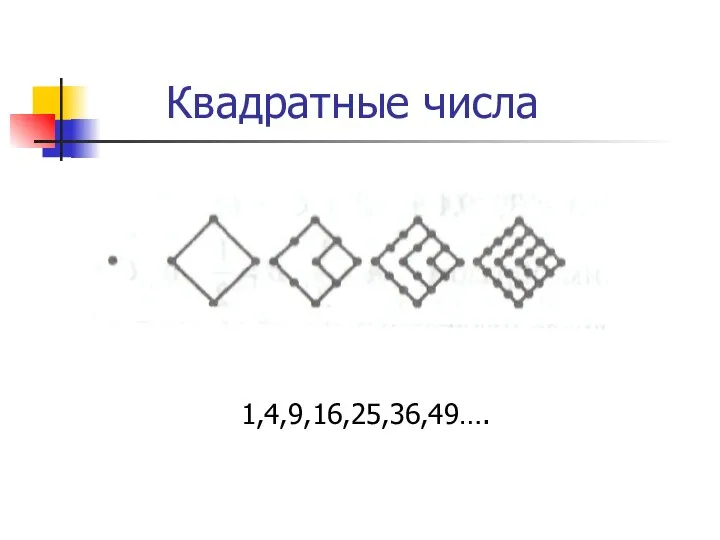
- 10. Квадратные числа 1,4,9,16,25,36,49….
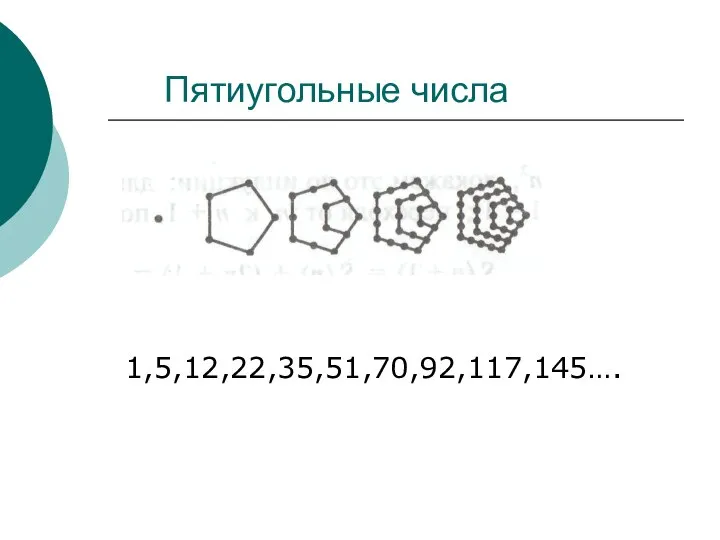
- 11. Пятиугольные числа 1,5,12,22,35,51,70,92,117,145….
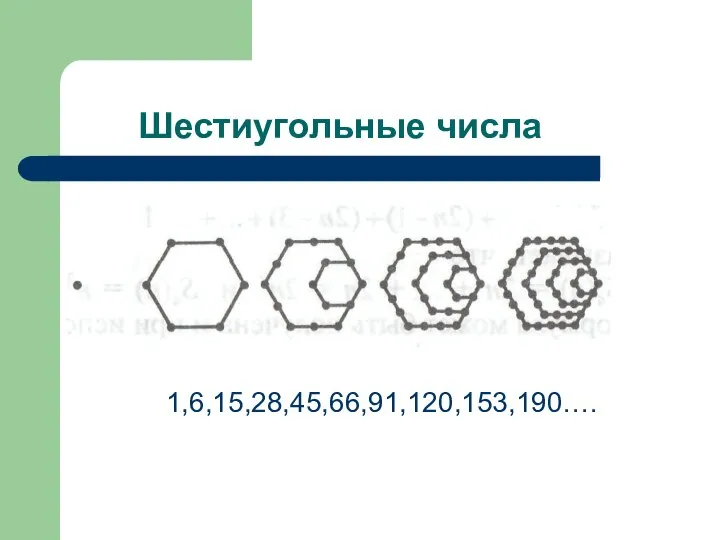
- 12. Шестиугольные числа 1,6,15,28,45,66,91,120,153,190….
- 13. Семиугольные числа 1,7,18,34,55,81,112,148,189,235…. Восьмиугольные числа 1,8,21,40,65,96,133,176,225,280….
- 14. Таким образом, треугольные числа получаются как последовательные суммы элементов последовательности 1,2, 3, ...; квадратные числа -
- 15. Гипоксил Александрийский (II в до н.э) N-ым m-угольным числом S(n) называется сумма n членов последовательности 1,
- 17. Пирамидальные числа
- 19. Скачать презентацию











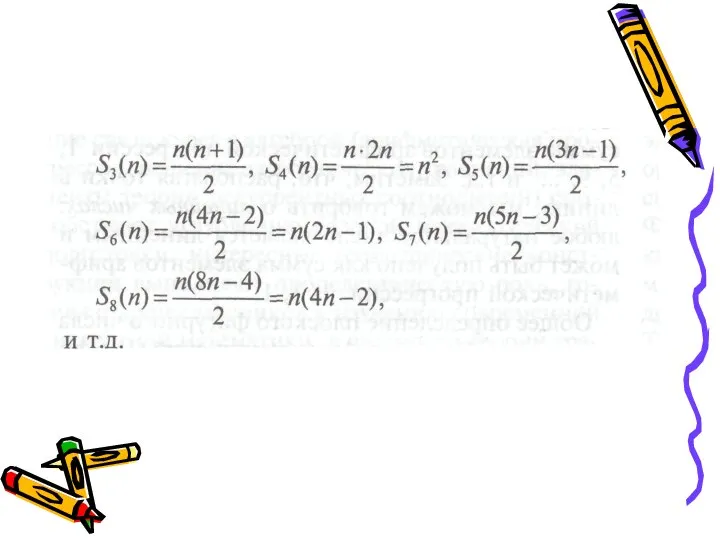

 Бально-рейтинговая система оценивания внеучебных достижений учащихся
Бально-рейтинговая система оценивания внеучебных достижений учащихся Мастер-класс Космическая ракета
Мастер-класс Космическая ракета Современные здоровьесберегающие технологии в педагогическом процессе ДОУ
Современные здоровьесберегающие технологии в педагогическом процессе ДОУ Обеспечение дифференцированного подхода к обучению с помощью разноуровневых заданий
Обеспечение дифференцированного подхода к обучению с помощью разноуровневых заданий Пальчиковые игры. Морские обитатели
Пальчиковые игры. Морские обитатели Требования к игровой деятельности
Требования к игровой деятельности Игровая программа Все работы хороши – выбирай на вкус!
Игровая программа Все работы хороши – выбирай на вкус! Конкурс Одаренные дети
Конкурс Одаренные дети Нарушение письма и чтения (НПЧ) – проблема современной школы
Нарушение письма и чтения (НПЧ) – проблема современной школы Выжить в походных условиях. Знания, которые нужны для жизни в походных условиях
Выжить в походных условиях. Знания, которые нужны для жизни в походных условиях Учитель года 2013
Учитель года 2013 Отчет о проведении мероприятий, посвящённых Всероссийскому дню правовой помощи детям в средне-старшей группе Ладушки
Отчет о проведении мероприятий, посвящённых Всероссийскому дню правовой помощи детям в средне-старшей группе Ладушки 12 апреля - всемирный день авиации и космонавтики
12 апреля - всемирный день авиации и космонавтики Весёлая зарядка. Физкультминутка
Весёлая зарядка. Физкультминутка Как эффективно развить интеллект ребенка
Как эффективно развить интеллект ребенка Професії майбутньго
Професії майбутньго Школьный экологический клуб ЭкоТворцы
Школьный экологический клуб ЭкоТворцы Сторителлинг. Технология Сторителлинг
Сторителлинг. Технология Сторителлинг Что? Где? Когда?
Что? Где? Когда? Фроттаж
Фроттаж Облыстық жас туристер станциясының туристік спорт бөлімінің қосымша білім беру педагогы
Облыстық жас туристер станциясының туристік спорт бөлімінің қосымша білім беру педагогы Новогоднее Поле чудес
Новогоднее Поле чудес Система педагогических наук
Система педагогических наук Создание книжки-малышки. Совместный проект с родителями
Создание книжки-малышки. Совместный проект с родителями Метод проектов на уроках технологии
Метод проектов на уроках технологии Социальное партнерство вуза и детского лагеря как ресурс преодоления аксиологической незрелости студентов-вожатых
Социальное партнерство вуза и детского лагеря как ресурс преодоления аксиологической незрелости студентов-вожатых Моим любознательным, немного озорным, самым добрым и искренним ученикам посвящается…
Моим любознательным, немного озорным, самым добрым и искренним ученикам посвящается… Этапы творческого проекта
Этапы творческого проекта