Содержание
- 2. Нулевой (основной) называют выдвинутую гипотезу. Конкурирующей (альтернативной) называют гипотезу, которая противоречит нулевой.
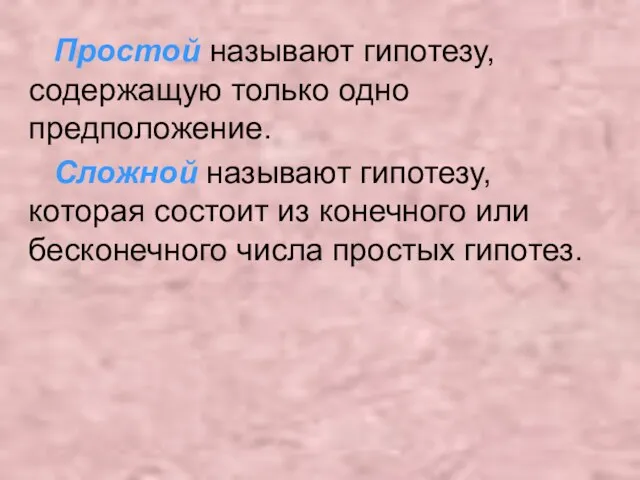
- 3. Простой называют гипотезу, содержащую только одно предположение. Сложной называют гипотезу, которая состоит из конечного или бесконечного
- 4. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода -в том,
- 5. Вероятность совершить ошибку первого рода принято обозначать через ; её называют уровнем значимости.
- 6. Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия Для проверки нулевой гипотезы используют специально подобранную случайную
- 7. Статистическим критерием (или просто критерием) называют случайную величину K, которая служит для проверки нулевой гипотезы.
- 8. Наблюдаемым значением называют значение критерия, вычисленное по выборкам.
- 9. Теоретическим значением называют значение критерия, вычисленное согласно нулевой гипотезе.
- 10. Критическая область. Область принятия гипотезы. Критические точки. Критической областью называют совокупность значений критерия, при которых нулевую
- 11. Основной принцип проверки статистических гипотез : Если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают,
- 12. Критическими точками (границами) называют точки, отделяющие критическую область от области принятия гипотезы.
- 13. Правосторонней называют критическую область, определяемую неравенством К > kкр , где kкр > 0. Левосторонней называют
- 14. Дополнительные сведения о выборе критической области. Мощность критерия Мощностью критерия называют вероятность попадания критерия в критическую
- 15. Другими словами, мощность критерия есть вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза.
- 16. Замечание 1. Поскольку вероятность события «ошибка второго рода допущена» равна β, то вероятность противоположного события «ошибка
- 17. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона. Если закон распределения неизвестен, но есть
- 18. Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
- 19. Критерий Пирсона основан на сравнении эмпирических (наблюдаемых) и теоретических (вычисленных в предположении о виде распределения) частот.
- 20. Пусть по выборке объёма n получено эмпирическое распределение: варианты…… xi x1 x2 x3 … эмп.частоты... ni
- 21. В качестве критерия проверки нулевой гипотезы примем случайную величину
- 22. Доказано, что при закон распределения случайной величины независимо от того, какому закону распределения подчинена генеральная совокупность,
- 23. Число степеней свободы находят по равенству k = m – 1 – r, где m –
- 24. В частности, если предполагаемое распределение – нормальное, то оценивают два параметра, поэтому r = 2 и
- 25. Правило. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу H0: генеральная совокупность распределена нормально,
- 26. По таблице критических точек распределения , по заданному уровню значимости α и числу степеней свободы k
- 27. Гипотеза о нормальном распределении случайной величины – рост случайно выбранного человека Экономический факультет, 2009год
- 28. Исходные данные Выборка роста студентов и критерий значимости ά=0,01
- 29. Шаг первый - оценки параметров распределения по выборке n=93 среднее=171,8710 s=8,833
- 30. Шаг второй Определяем наименьшее 156 см и наибольшее 195 см значения вариант
- 31. Шаг третий Определяем m -число интервалов(не менее 4). Возьмем m=7
- 32. Шаг 4 Определяем длину конечных промежутков (195-156)/7=5,57; для удобства возьмем расстояние между точками 5,75.
- 33. Шаг 5 Используя найденную длину, определяем концы промежутков
- 34. Шаг 6 и далее Оформим в виде таблицы
- 35. Исходная таблица
- 36. Подсчитываем эмпирические частоты по выборке
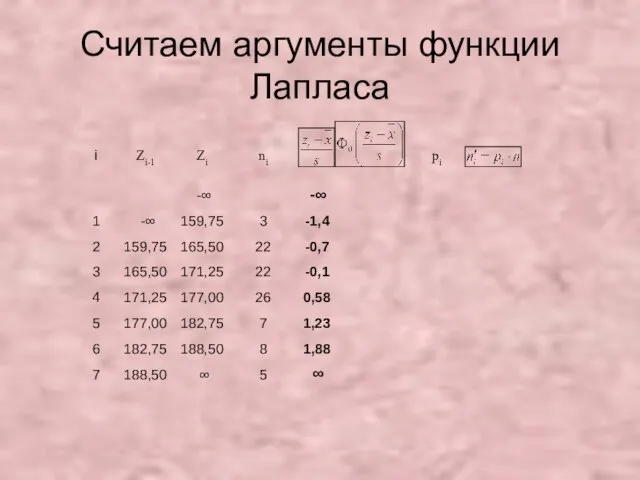
- 37. Считаем аргументы функции Лапласа
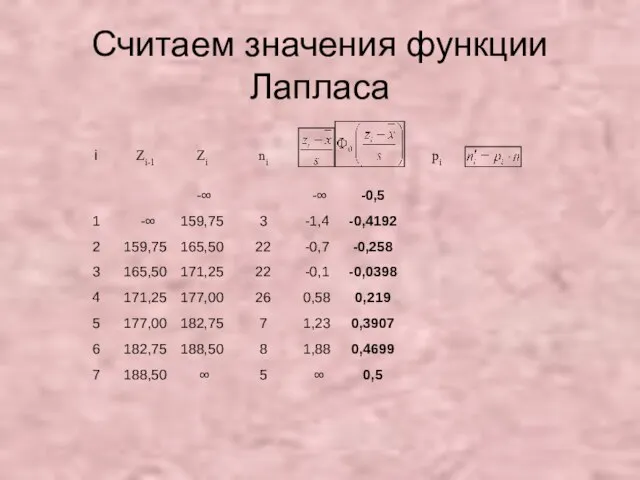
- 38. Считаем значения функции Лапласа
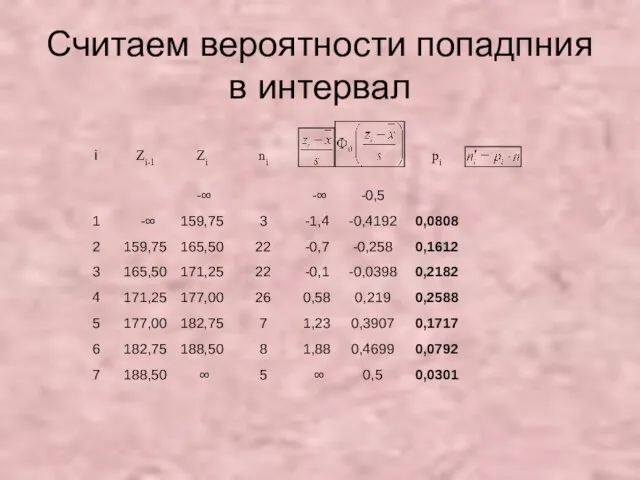
- 39. Считаем вероятности попадпния в интервал
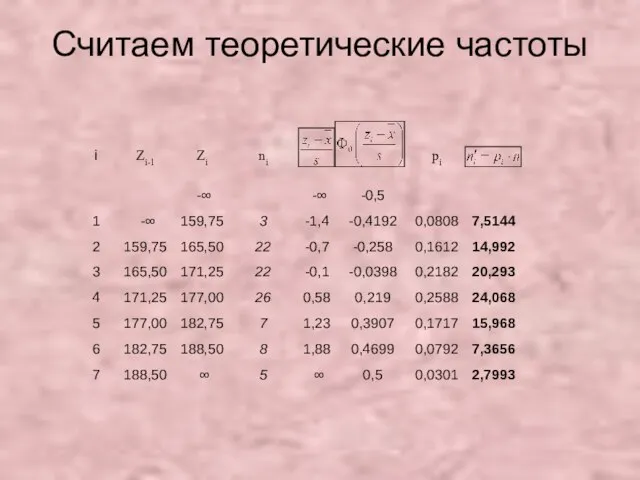
- 40. Считаем теоретические частоты
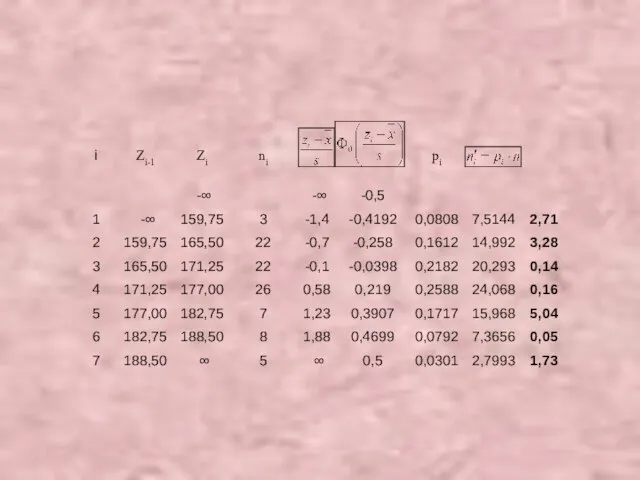
- 41. Считаем
- 43. Находим наблюдаемое значение критерия по формуле
- 44. Находим критическое значение По уровню значимости ά=0,05 и числу степеней свободы k=m-3=7-3= 4 Kкр=9,5
- 45. ВЫВОД Kнабл>Kкр – гипотезу отвергаем с вероятностью 0,05 совершить ошибку первого рода.
- 46. Цепь Маркова
- 47. Пусть некоторая система в каждый момент времени находится в одном из k состояний: первом, втором,…, k-м.
- 48. Цепью Маркова называют последовательность испытаний, в каждом из которых система принимает только одно из k состояний
- 49. Цепью Маркова с дискретным временем называют цепь, изменение состояний которой происходит в определённые фиксированные моменты времени.
- 50. Однородная цепь Маркова. Переходные вероятности. Матрица перехода. Однородной называют цепь Маркова, если условная вероятность pij (s)
- 51. Пример (случайное блуждание). Пусть на прямой Ox в точке с целочисленной координатой x = n находится
- 52. Переходной вероятностью pij называют условную вероятность того, что из состояния i (в котором система оказалась в
- 53. Пусть число состояний конечно и равно k. Матрицей перехода системы называют матрицу, которая содержит все переходные
- 54. Пример матрицы перехода системы, которая может находиться в трёх состояниях: Здесь p11 = 0,5 – вероятность
- 55. Равенство Маркова Обозначим через pij(n) вероятность того, что в результате n шагов (испытаний) система перейдёт из
- 56. Из первоначального состояния i за m шагов система перейдёт в промежуточное состояние r с вероятностью Pir(m),
- 57. Пусть n=2, m=1 в равенстве Маркова тогда или
- 58. Таким образом, по данной формуле можно найти все вероятности Pij(2) , следовательно, и саму матрицу Г2.
- 59. Пример. Задана матрица перехода Найти матрицу перехода: :
- 61. Скачать презентацию


















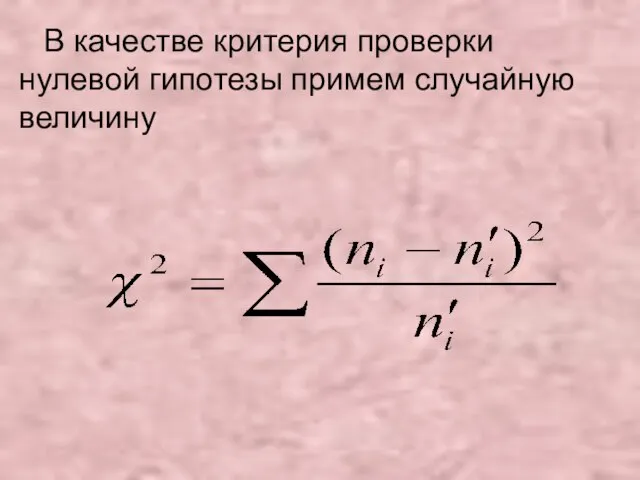















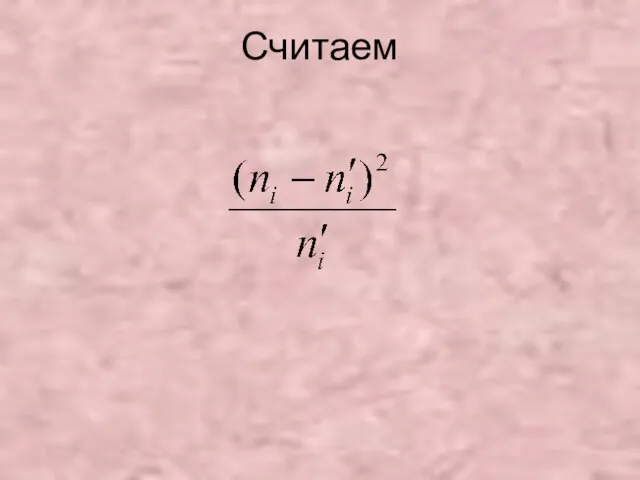
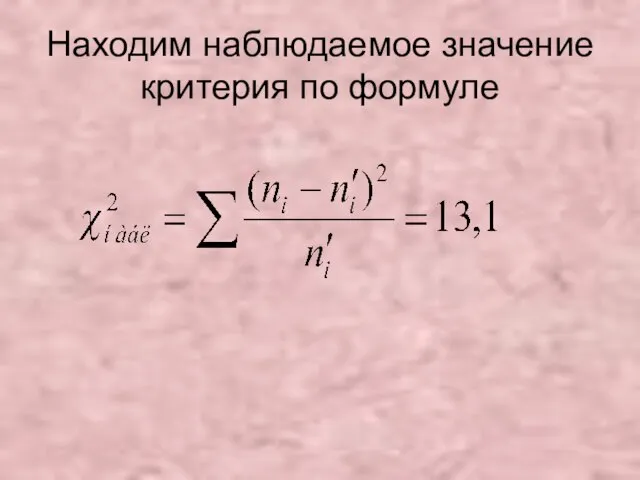
















 Проблемы умственного воспитания в трудах зарубежных педагогов
Проблемы умственного воспитания в трудах зарубежных педагогов Папа, мама, я - дружная семья! Младшая группа
Папа, мама, я - дружная семья! Младшая группа Дружба - великая сила
Дружба - великая сила Детский сад
Детский сад Справочник классного руководителя
Справочник классного руководителя Внедрение модели проектирования развивающей предметнопространственной среды в учреждениях дошкольного образования
Внедрение модели проектирования развивающей предметнопространственной среды в учреждениях дошкольного образования Виды конструкционных материалов (технология, 5 класс)
Виды конструкционных материалов (технология, 5 класс) Скворечник своими руками
Скворечник своими руками Арт-объект из природного материала
Арт-объект из природного материала Подготовка к контрольной работе по литературе в 5 классе
Подготовка к контрольной работе по литературе в 5 классе Игры для развития познавательных процессов
Игры для развития познавательных процессов Значение дней воинской славы России для понимания государства Российского
Значение дней воинской славы России для понимания государства Российского Ткани и их виды (1 класс)
Ткани и их виды (1 класс) Подготовка КДР. Краевая диагностическая работа
Подготовка КДР. Краевая диагностическая работа Вода вокруг нас
Вода вокруг нас Роль игры в развитии детей дошкольного возраста
Роль игры в развитии детей дошкольного возраста Основы научных исследований. Лекция 1
Основы научных исследований. Лекция 1 Квест- игра Большие гонки по правилам
Квест- игра Большие гонки по правилам Родительское собрание. Воспитаем вместе. (1 класс)
Родительское собрание. Воспитаем вместе. (1 класс) Тюльпан из фетра
Тюльпан из фетра Гласные буквы Я, я
Гласные буквы Я, я Экспериментальная деятельность. Как ржавел Железный дровосек
Экспериментальная деятельность. Как ржавел Железный дровосек Открытка папе. Урок технологии в начальной школе; изготовление открытки ко Дню защитника отечества
Открытка папе. Урок технологии в начальной школе; изготовление открытки ко Дню защитника отечества Применение кроссенса в практической работе педагога
Применение кроссенса в практической работе педагога Первая младшая группа
Первая младшая группа Семена и фантазии (1 класс)
Семена и фантазии (1 класс) Лепка из соленого теста
Лепка из соленого теста Составление рассказа по сюжетной картинке
Составление рассказа по сюжетной картинке