1. Расчет фазовых превращений в металлах и сплавах В работе предложены аналитические выражения для расчета критических темпер

Энергия образования кристаллического вещества равна :
Уравнения (3,4) позволяют рассчитать также координационные числа атомов
в жидких и твердых фазах, образующиеся при нагреве или охлаждении металла,
а также их изменения при фазовых переходах.
При температурах фазовых переходов, когда устанавливается критическое расстояние между соседними ионами, должно выполнятся следующее условие :
:
Расчет температур фазовых переходов в чистых металлах :
где:
где: - температуры испарения, плавления и полиморфного превращения.

• Выражения (1-6) применимы и для расчета фазовых превращений в сплавах. В этом случае энергии связи атомов и тепловые эффекты превращений будут зависимыми, кроме температуры, также и от состава фаз.
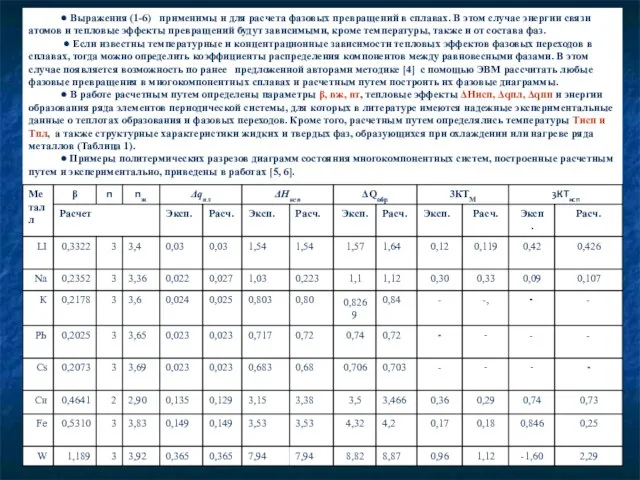
• Если известны температурные и концентрационные зависимости тепловых эффектов фазовых переходов в сплавах, тогда можно определить коэффициенты распределения компонентов между равновесными фазами. В этом случае появляется возможность по ранее предложенной авторами методике [4] с помощью ЭВМ рассчитать любые фазовые превращения в многокомпонентных сплавах и расчетным путем построить их фазовые диаграммы.
• В работе расчетным путем определены параметры β, nж, nт, тепловые эффекты ΔНисп, Δqпл, Δqпп и энергии образования ряда элементов периодической системы, для которых в литературе имеются надежные экспериментальные данные о теплотах образования и фазовых переходов. Кроме того, расчетным путем определялись температуры Тисп и Тпл, а также структурные характеристики жидких и твердых фаз, образующихся при охлаждении или нагреве ряда металлов (Таблица 1).
• Примеры политермических разрезов диаграмм состояния многокомпонентных систем, построенные расчетным путем и экспериментально, приведены в работах [5, 6].

2. Расчет фазовых равновесий в трехкомпонентных
металлических системах
Существующие методы термодинамического расчета фазовых равновесий и построения диаграмм состояния не позволяют количественно описать процесс формирования фазового состава и структуры конкретных сплавов заданного состава.
В работе получены аналитические зависимости между составами исходных сплавов, составами и относительными количествами равновесных фаз и коэффициентами распределения компонентов, позволяющие рассчитать составы и относительные количества фаз в зависимости от температуры и состава исходного сплава (число компонентов сплава n= 2,3, …N) .
• Состав жидкой фазы Хn (n=А,В,С индексы компонентов) рассчитывается:
• Состав твердой фазы, находящейся в равновесии с жидкой при заданной температуре, определяется, как:
где:
- грамм-атомные доли компонентов А, В и С в твердой (α) и жидкой (Ж) фазах,
- грамм-атомные доли компонентов А, В и С в исходном сплаве.
• Относительные количества твердой
и жидкой (1-
)
фаз
можно определить из уравнении:
• Например, при кристаллизации тройных твердых растворов
температуры ликвидуса и солидуса определяются из условий:
где:

Расчет процесса кристаллизации многокомпонентных твердых растворов,
где число компонентов n>3
Для многокомпонентных систем в случае двухфазных равновесий α+ж
зависимости между составами исходного сплава
, жидкой
и твердой
фазами, а также коэффициентами распределения компонентов также имеют вид:
где: i – индекс компонента сплава (i=1÷n):
αT - относительное количество твердой фазы при заданной температуре Т0К.
Для определения относительной доли твердой фазы αТ:
Определяя концентрационные и температурные зависимости коэффициентов распределенияв многокомпонентных сплавах независимыми способами, из уравнений () можно найти долю равновесных твердой (αТ) и жидкой (1-αТ) фаз при любой температуре, рассчитать их составы и определить положения конод.
Температуры ликвидуса и солидуса многокомпонентных сплавов также могут быть определены из условий:

4 Расчет неравновесной кристаллизации твердых растворов
При разработке метода расчета весь процесс неравновесной кристаллизации сплава рассматривается как сумма начальных моментов кристаллизации набора сплавов, составы которых соответствуют составу жидкой фазы, остающейся после каждой стадии кристаллизации. Согласно теории Бартона, Прим и Слихтора на границе кристалл - жидкий раствор имеет место равновесие между жидкой и твердой фазами. Тогда первые кристаллы твердой фазы на любой стадии процесса кристаллизации будут иметь составы, соответствующие равновесной диаграмме состояния. В этом случае для любой стадии процесса неравновесной кристаллизации можно использовать уравнения, полученные для случая равновесной кристаллизации сплавов. При этом необходимо только знание зависимостей равновесных коэффициентов распределения компонентов сплава от температуры.
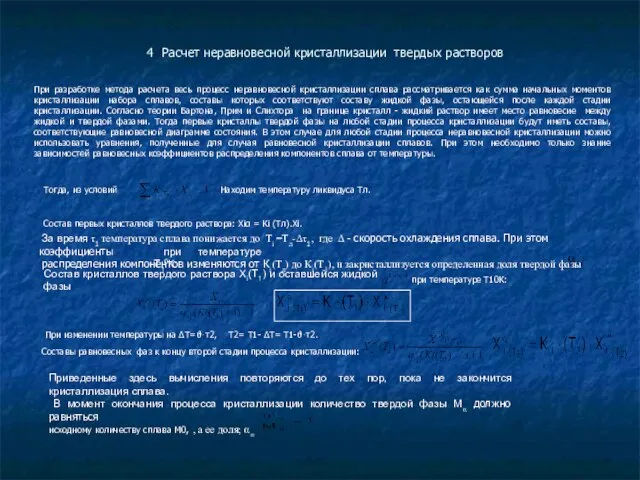
Тогда, из условий
Находим температуру ликвидуса Тл.
Состав первых кристаллов твердого раствора: Хiα = Кi (Тл).Хi.
За время τ1 температура сплава понижается до Тi =Тл-Δτ1, где Δ - скорость охлаждения сплава. При этом коэффициенты
распределения компонентов изменяются от Кi(Тл) до Кi(Т1), и закристаллизуется определенная доля твердой фазы
.
Состав кристаллов твердого раствора Хi(Т1) и оставшейся жидкой фазы
при температуре Т10К:
при температуре Т10К:
При изменении температуры на ΔТ=ϑ⋅τ2, Т2= Т1- ΔТ= Т1-ϑ⋅τ2.
Составы равновесных фаз к концу второй стадии процесса кристаллизации:
Приведенные здесь вычисления повторяются до тех пор, пока не закончится кристаллизация сплава.
В момент окончания процесса кристаллизации количество твердой фазы Мα должно равняться
исходному количеству сплава М0, , а ее доля; α=
.

Выводы:
Для расчета общего количества твердой фазы m-αn и ее относительной доли Sn после n-й стадий процесса кристаллизации:
m-αn= m-α1+ m-α2+…+ m-αn ,
Sn= α1+(1- α1)α2+(1- α1) (1- α2) α3+…+(1- α1) (1- α2)… (1- αn-1) αn .
Температуру при которой Sn становится равной единице, примем за температуру неравновесного солидуса. Общее время кристаллизации сплава (τ0) при заданной скорости охлаждения ϑ равно: τ0=(Тлик-Тсолид) ϑ.
1.Предложен метод расчета фазовых равновесий в многокомпонентных металлических системах и построения их диаграмм состояния, основанный на впервые сформулированных условиях определения критических точек фазовых превращений с использованием температурных и концентрационных зависимостей коэффициентов распределения компонентов. Установлены аналитические зависимости между коэффициентами распределения компонентов, средним химическим составом сплавов, составом и относительными количествами равновесных фаз. Предложенный метод позволяет количественно описать процесс формирования фазового состава и структуры сплавов при равновесных и неравновесных условиях охлаждения.
2. Предложены математические модели изменения избыточных химических потенциалов компонентов при фазовых переходах и произведения растворимостей компонентов при выделении кристаллов химических соединений в сплавах систем на основе алюминия и меди. Разработаны программы расчета фазовых превращений в равновесных и неравновесных условиях охлаждения.
3. Расчетным методом, а также методами микроскопического, дифференциально-термического и микрорентгеноспектрального анализов исследованы фазовые равновесия в сплавах систем Al-Cu-Si, Al-Ni-Si, Al-Si-Cu-Ni. Показано хорошее соответствие между расчетными и опытными данными.Впервые установлено, что в сплавах изученных систем имеет место ряд безвариантных эвтектических и перитектических превращений. Уточнены положения критических точек.