Содержание
- 2. Умножение:
- 3. Деление: 1.Выяснить степень частного 2.Выяснить степень остатка
- 4. Многочлены называются тождественно равными, если при всех значениях переменной их значения совпадают (их разность при всех
- 5. У равных многочленов равны коэффициенты при соответствующих степенях переменной. Доказательство: 1.Если коэффициенты при соответствующих степенях переменной
- 6. 2. Если многочлены тождественно равны, то и коэффициенты при соответствующих значениях х равны. Дано: Доказать: ;
- 8. Скачать презентацию
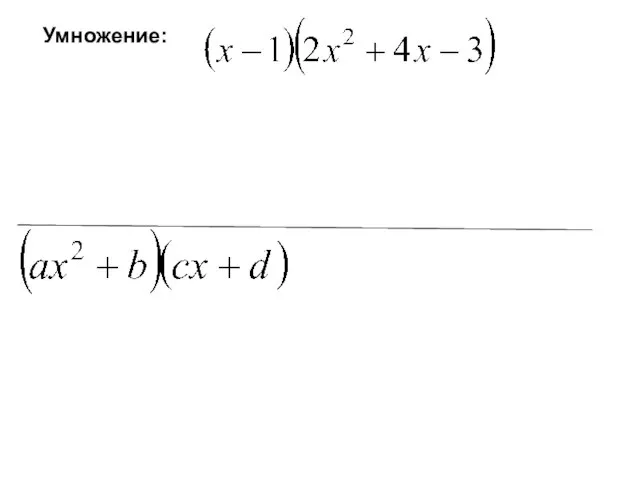




 Породы кроликов
Породы кроликов Орехоплодовые сосны. Достижения и перспективы в центрально-черноземном регионе
Орехоплодовые сосны. Достижения и перспективы в центрально-черноземном регионе Моделирование как метод познания
Моделирование как метод познания НПО «Криста»
НПО «Криста» Ахроматическая гармония. Общие принципы построения композиции. Занятие №4
Ахроматическая гармония. Общие принципы построения композиции. Занятие №4 Визитная карточка начальной школы ГУО «Гимназия №20 г.Минска»
Визитная карточка начальной школы ГУО «Гимназия №20 г.Минска» ПЕРМСКИЙ КАДЕТСКИЙ КОРПУС
ПЕРМСКИЙ КАДЕТСКИЙ КОРПУС Голливудский макияж. Классика, которая всегда уместна
Голливудский макияж. Классика, которая всегда уместна Скульптура Санкт-Петербурга
Скульптура Санкт-Петербурга На родине Астафьева
На родине Астафьева  Автор: Жаринов Николай Викторович, учитель истории МОУ «Васильчуковская СОШ» МОУ «Васильчуковская СОШ» Ключевского района, Алтай
Автор: Жаринов Николай Викторович, учитель истории МОУ «Васильчуковская СОШ» МОУ «Васильчуковская СОШ» Ключевского района, Алтай Архитектура западноевропейского средневековья
Архитектура западноевропейского средневековья Стекловолокно. Получение стекловолокна
Стекловолокно. Получение стекловолокна به نام خدا
به نام خدا The simple or indefinite past tense in Lithuanian. Simplified view of the past tense conjugation in Lithuanian
The simple or indefinite past tense in Lithuanian. Simplified view of the past tense conjugation in Lithuanian Техника борьбы лёжа. Удержания
Техника борьбы лёжа. Удержания Россия! Роса и сила и синее что-то
Россия! Роса и сила и синее что-то «Поспорили однажды корень, стебель, лист – кто из них важнее?»
«Поспорили однажды корень, стебель, лист – кто из них важнее?» Наследственные болезни 9 класс
Наследственные болезни 9 класс Концепция проведения ежегодного всероссийского слёта юных туристов в 2020 году
Концепция проведения ежегодного всероссийского слёта юных туристов в 2020 году Реклама instagram. Макет рекламы
Реклама instagram. Макет рекламы Психология профессиональной карьеры
Психология профессиональной карьеры Сжатие текста Урок русского языка, 9 класс, подготовка к ГИА 9
Сжатие текста Урок русского языка, 9 класс, подготовка к ГИА 9 Практикум по решению задач. Природа и основные свойства цвета
Практикум по решению задач. Природа и основные свойства цвета Презентация на тему Святые войны
Презентация на тему Святые войны  Развивающая программа
Развивающая программа Детские зарисовки
Детские зарисовки Изделие Волшебные фигурки
Изделие Волшебные фигурки