Содержание
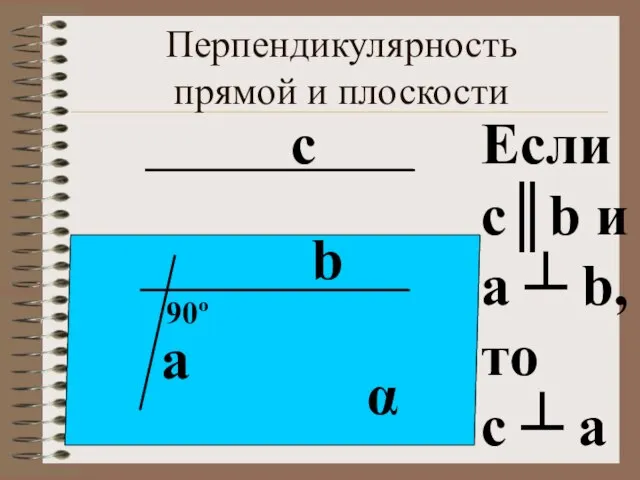
- 2. Перпендикулярность прямой и плоскости α а b Если с║b и а ┴ b, то с ┴
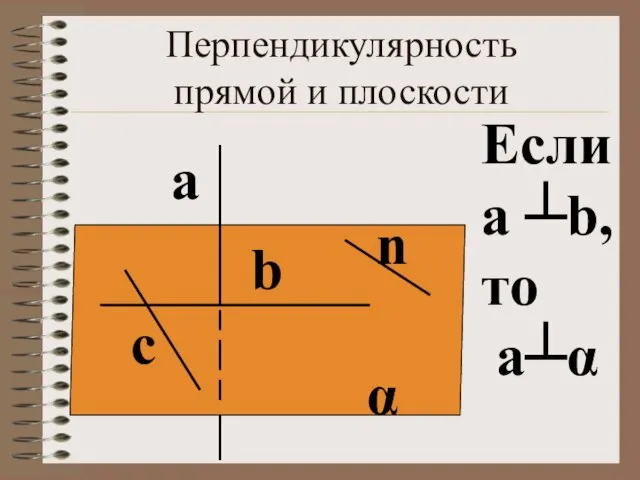
- 3. Перпендикулярность прямой и плоскости α а b Если а ┴b, то а┴α с n
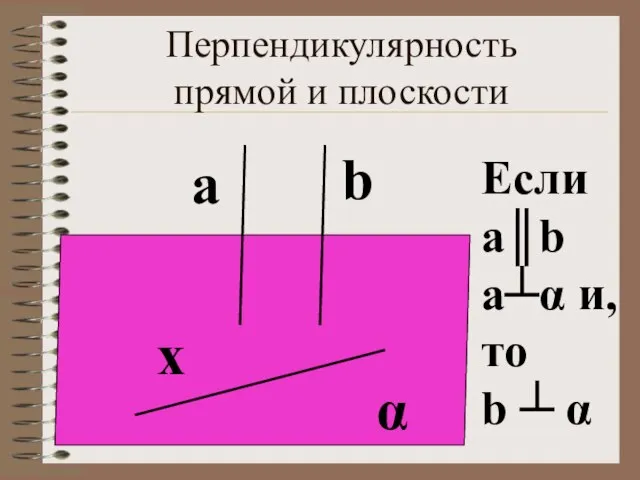
- 4. Перпендикулярность прямой и плоскости α b Если а║b а┴α и, то b ┴ α а x
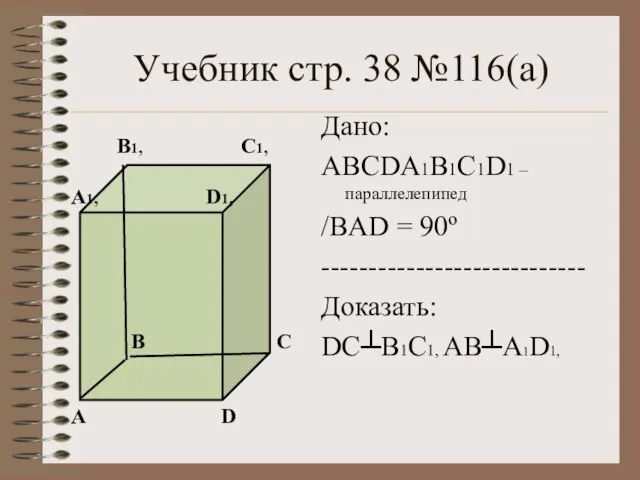
- 5. Учебник стр. 38 №116(а) Дано: ABCDA1B1C1D1 – параллелепипед /BАD = 90º ---------------------------- Доказать: DC┴B1C1, АВ┴А1D1, А
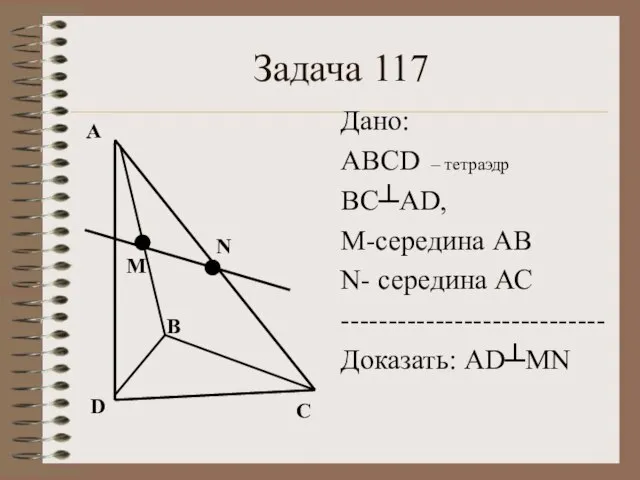
- 6. Задача 117 А В С D М N Дано: ABCD – тетраэдр ВС┴AD, М-середина АВ N-
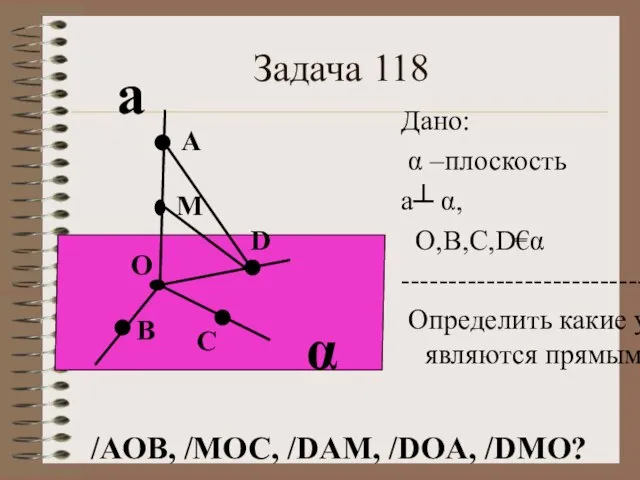
- 7. Задача 118 α а О М А Дано: α –плоскость а┴ α, О,В,С,D€α ---------------------------- Определить какие
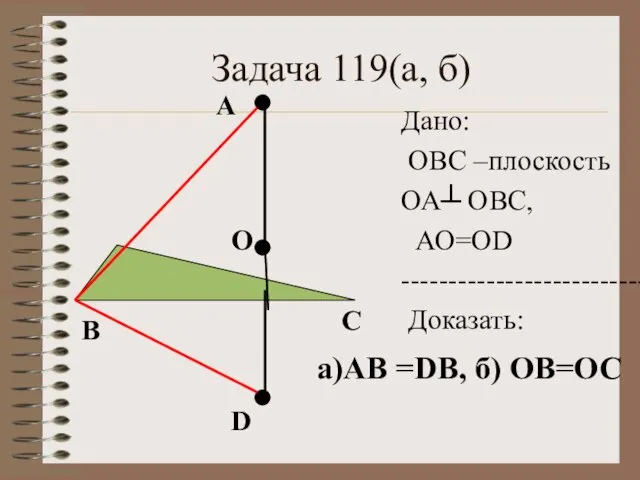
- 8. Задача 119(а, б) О А Дано: ОВС –плоскость ОА┴ ОВС, АО=ОD ---------------------------- Доказать: B C D
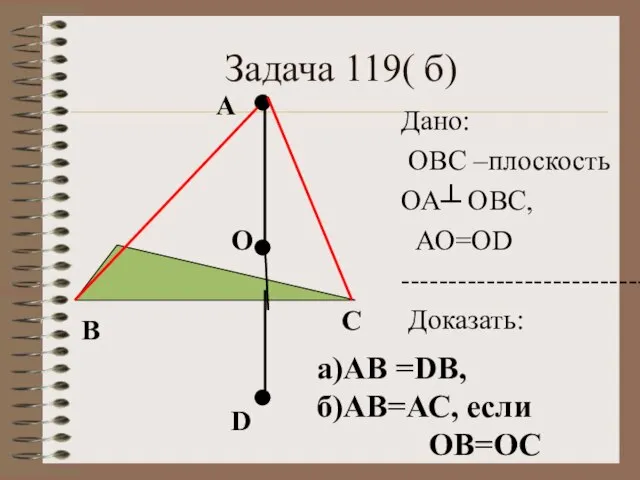
- 9. Задача 119( б) О А Дано: ОВС –плоскость ОА┴ ОВС, АО=ОD ---------------------------- Доказать: B C D
- 11. Скачать презентацию
 Международная коммерческая сделка и способы ее оформления Понятие международной коммерческой сделки, классификация сделок Спос
Международная коммерческая сделка и способы ее оформления Понятие международной коммерческой сделки, классификация сделок Спос Переносные окрасочные агрегаты для окраски масляными составами
Переносные окрасочные агрегаты для окраски масляными составами Основы теории права. Понятие права и его признаки
Основы теории права. Понятие права и его признаки СТАТИСТИКА ЗДОРОВЬЯ В КЫРГЫЗСКОЙ РЕСПУБЛИКЕ
СТАТИСТИКА ЗДОРОВЬЯ В КЫРГЫЗСКОЙ РЕСПУБЛИКЕ Гимнастика
Гимнастика Всероссийская перепись: вчера и сегодня
Всероссийская перепись: вчера и сегодня ??
?? «Только живите достойно благовествования Христова, чтобы мне, приду ли я и увижу вас, или не приду, слышать о вас, что вы стоите в одн
«Только живите достойно благовествования Христова, чтобы мне, приду ли я и увижу вас, или не приду, слышать о вас, что вы стоите в одн Живопись
Живопись Балясины
Балясины «И снизу лед…»
«И снизу лед…» Масленица в «Берегине» фотоотчёт о поездке в Бердск 2 класс Б МБОУ Гимназия №4 классный руководитель: Аникина Н.А.
Масленица в «Берегине» фотоотчёт о поездке в Бердск 2 класс Б МБОУ Гимназия №4 классный руководитель: Аникина Н.А.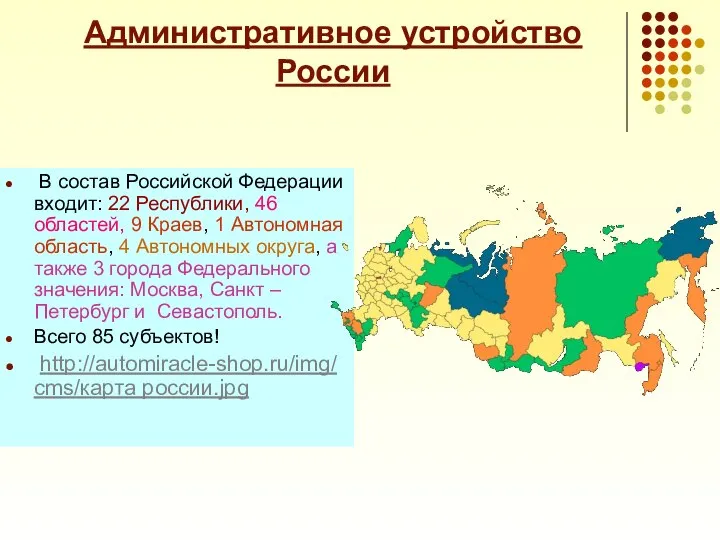 Административное устройство России
Административное устройство России Альтернативна програма інвестування
Альтернативна програма інвестування Презентация на тему семейный бюджет основа
Презентация на тему семейный бюджет основа  Программа посткризисного восстановления (оздоровление конкурентоспособных предприятий)
Программа посткризисного восстановления (оздоровление конкурентоспособных предприятий) Презентация на тему ПСКОВ – ГОРОД ВОИНСКОЙ СЛАВЫ
Презентация на тему ПСКОВ – ГОРОД ВОИНСКОЙ СЛАВЫ  Презентация на тему Что такое биосфера и как она устроена
Презентация на тему Что такое биосфера и как она устроена Организация простых работ по техническому обслуживанию и ремонту электрического оборудования. Электрические аппараты
Организация простых работ по техническому обслуживанию и ремонту электрического оборудования. Электрические аппараты Экстремумы функции
Экстремумы функции Модернизация литейного производства
Модернизация литейного производства Психолого - педагогическое сопровождение учащихся в период адаптации
Психолого - педагогическое сопровождение учащихся в период адаптации Тело человека
Тело человека Презентация на тему Славянская мифология
Презентация на тему Славянская мифология  Лидерство
Лидерство Причины нарушения осанки школьников
Причины нарушения осанки школьников ВЫБОР ПРОФЕССИИ - ОСНОВА ЖИЗНЕННОГО УСПЕХА
ВЫБОР ПРОФЕССИИ - ОСНОВА ЖИЗНЕННОГО УСПЕХА Екатерина Гильфанова, дайвер с 15 летним стажем
Екатерина Гильфанова, дайвер с 15 летним стажем