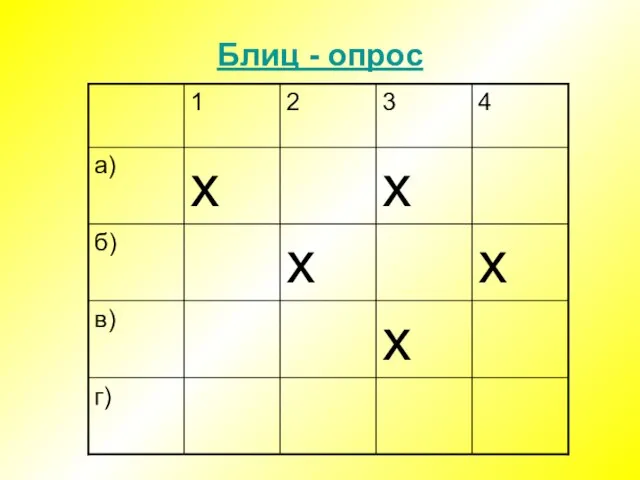
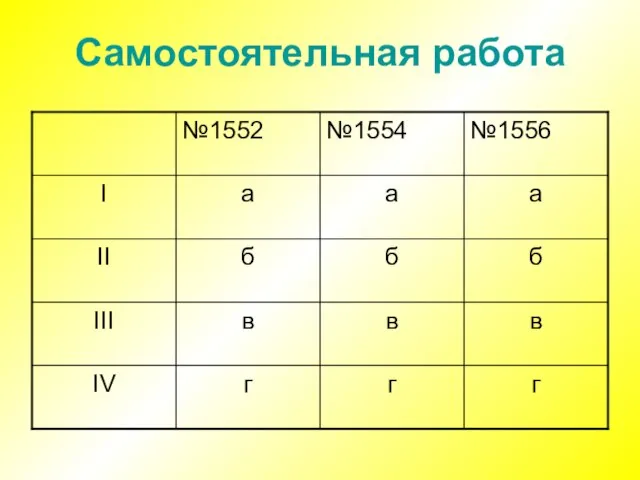
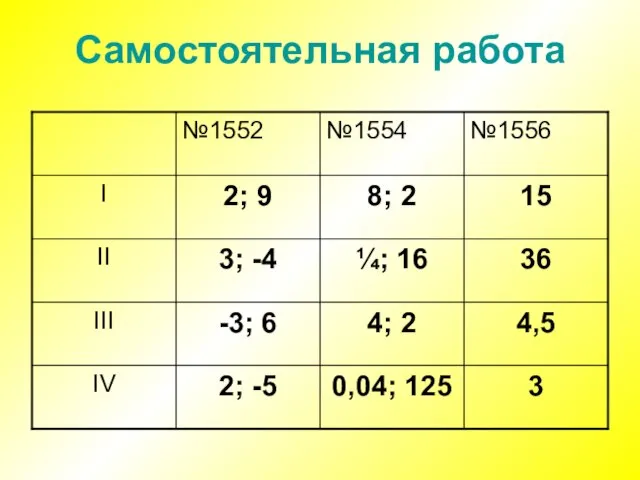
Слайд 3Блиц - опрос
Какие из данных функций являются логарифмическими?
а) y= lg (2x+3)
б) y

= 43x-5
в) y = log 3 27 + 8x
г) y = log 5 125 – 4x3
2. Область определения логарифмической функции y= log2 (x-5) +2 :
а) (7; +∞)
б) (5; +∞)
в) (-∞; -5)
г) [5; +∞)
Слайд 43. Какие из данных функций являются возрастающими?
а) y= log2.5 (x+7)
б) y =

log 0.5 (x-5)
в) y = ln (2x+3)
г) y = log 2 4
4. Какая из записей является формулой перехода от логарифмов по основанию m к логарифмам по основанию n:
а) б)
в) ?
Слайд 5 Свойства логарифмов
log а а n log а b
log а а n
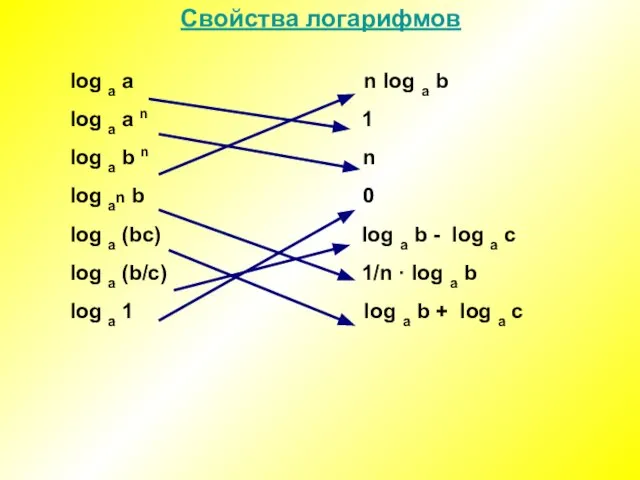
1
log а b n n
log аn b 0
log а (bc) log а b - log а c
log а (b/c) 1/n · log а b
log а 1 log а b + log а c
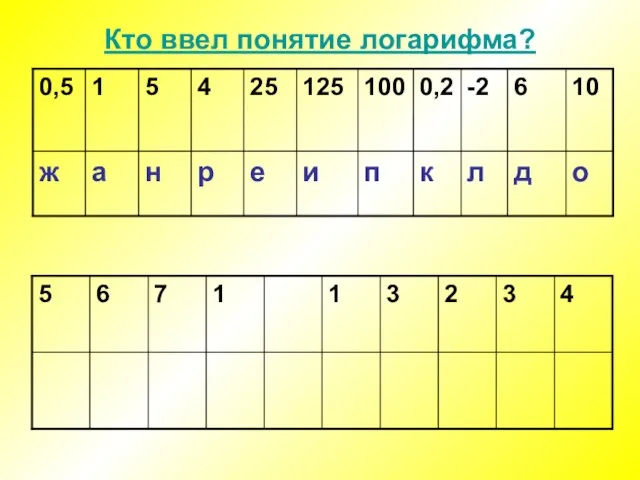
Слайд 8Джон Непер – шотландский математик, который впервые ввел понятие логарифма.
«Логарифм» -
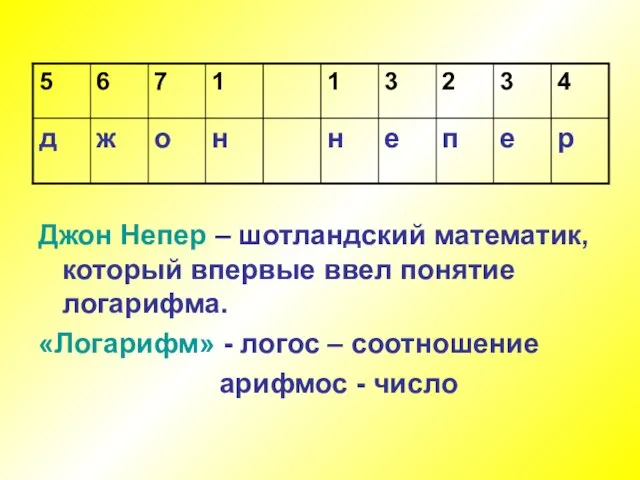
логос – соотношение
арифмос - число
Слайд 9 Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а

подчас и довольно тонкие ошибки
Мартин Гарднер
Слайд 10Логарифмическая комедия
«2 >3»
Рассмотрим неравенство
¼ > ⅛
(½)² > (½)³
Прологарифмируем по основанию 10
lg (½)²

> lg (½)³
2 lg (½) > 3lg (½)
Разделим обе части неравенства на lg (½)
2 >3







 Реформа языка Карамзина
Реформа языка Карамзина Варианты расчета бонуса за два месяца
Варианты расчета бонуса за два месяца Эксплуатация автомобильного транспорта
Эксплуатация автомобильного транспорта Государство в политической системе
Государство в политической системе ИСТОРИЯ СПИЧЕК
ИСТОРИЯ СПИЧЕК Презентация на тему Растения-индикаторы
Презентация на тему Растения-индикаторы Мышление как психический процесс. Виды и формы мышления. 4 формата мышления
Мышление как психический процесс. Виды и формы мышления. 4 формата мышления Субъекты правовых отношений. Правовое положение лиц
Субъекты правовых отношений. Правовое положение лиц скульптура «Под одними звездами» ("Unter den gleichen Sternen")
скульптура «Под одними звездами» ("Unter den gleichen Sternen") Виды гимнастики
Виды гимнастики Hilton Hotels & Resorts
Hilton Hotels & Resorts Шар. Елка. Снеговик
Шар. Елка. Снеговик Обзор православной литературы Доброе слово для малых ребят
Обзор православной литературы Доброе слово для малых ребят Водные маршруты
Водные маршруты Презентация на тему Василий Тёркин
Презентация на тему Василий Тёркин  Технология приготовления пиццы
Технология приготовления пиццы Мир в свечах Выполнила: Плаксунова Людмила МОУ СОШ №4 Руководитель: Чуприна Т.В.
Мир в свечах Выполнила: Плаксунова Людмила МОУ СОШ №4 Руководитель: Чуприна Т.В. "Поле - чудес" по произведениям К.И. Чуковского
"Поле - чудес" по произведениям К.И. Чуковского PURE_THERAPY_Bezuprechnaya_idealno_ochischennaya_kozha
PURE_THERAPY_Bezuprechnaya_idealno_ochischennaya_kozha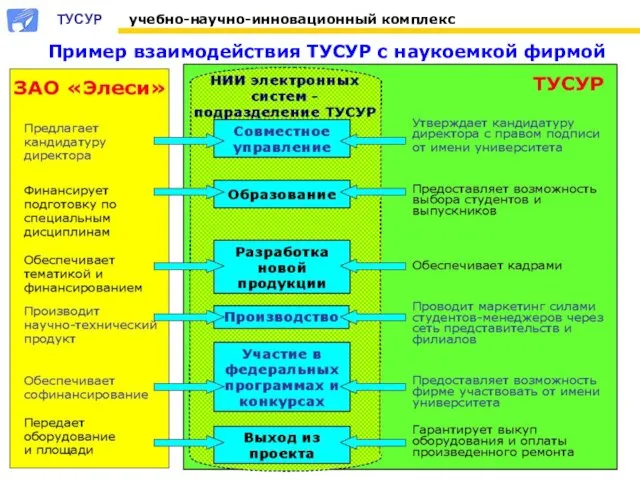 Пример взаимодействия ТУСУР с наукоемкой фирмой
Пример взаимодействия ТУСУР с наукоемкой фирмой Введение в менеджмент
Введение в менеджмент Австралия
Австралия Who should be the first ?
Who should be the first ? Велосипедный туризм
Велосипедный туризм Музей восстания машин
Музей восстания машин Презентация "Художники пореформенной России" - скачать презентации по МХК
Презентация "Художники пореформенной России" - скачать презентации по МХК Хочу отдыхать
Хочу отдыхать Сенситивные периоды человека (методика Марии Монтессори)
Сенситивные периоды человека (методика Марии Монтессори)