«Многогранники вокруг нас или мы внутри многогранника»

«Математика владеет не только истиной, но и высшей красотой - красотой отточенной и строгой, возвышенно чистой и стремящейся к подлинному совершенству, которое свойственно лишь величайшим образцам искусства.»
Бертран Рассел

Цели работы:
Познакомиться с многогранниками.
Показать влияние правильных многогранников на возникновение философских теорий и гипотез.
Показать связь геометрии и природы.
Познакомиться с примерами применения многогранников в архитектуре и искусстве.

Содержание:
Многогранники в природе.
Историческая справка.
Многогранники в искусстве.
Многогранники в архитектуре.

часть пространства, ограниченная совокупностью конечного числа плоских многоугольников, соединенных таким образом, что каждая сторона любого многоугольника является стороной ровно одного другого многоугольника (называемого смежным), причем вокруг каждой вершины существует ровно один цикл многоугольников.
МНОГОГРАННИК

Правильные многогранники имеют красивые формы.
Они являются удивительным символом симметрии, привлекавшим внимание выдающихся мыслителей.
Этим и объясняется интерес человека к многогранникам.

Многогранники в природе
"Природа вскармливает на своем лоне неисчерпаемое количество удивительных созданий, которые по красоте и разнообразию далеко превосходят все созданные искусством человека формы".
В книге немецкого биолога Э. Геккеля "Красота форм в природе"
можно прочитать такие строки:

По законам «строгой» архитектуры…
Пчёлы - удивительные создания.
Пчелиные соты представляют собой пространственный паркет и заполняют пространство так, что не остается просветов.
«Мой дом построен по законам самой строгой архитектуры. Сам Эвклид мог бы поучиться, познавая геометрию сот».
Как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»:

Простейшее животное
Скелет одноклеточного организма феодарии (Circogonia icosahedra) по форме напоминает икосаэдр. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя двенадцатью иглами, выходящими из 12 вершин скелета. Он больше похоже на звёздчатый многогранник.
Из всех многогранников с тем же числом граней икосаэдр имеет наибольший объём при наименьшей площади поверхности.
Это свойство помогает морскому организму преодолевать давление толщи воды.

Интересно
Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов.
Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр.

Чудо природы – кристаллы
куб передает форму кристаллов поваренной соли NaCl
монокристалл алюминиево-калиевых квасцов имеет форму октаэдра,
кристалл сернистого колчедана FeS имеет форму додекаэдра,
сернокислый натрий - тетраэдр,
бор - икосаэдр.
Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников:

Шеелит,5см, найден в Китае.
(блочное строение кристалла),
Геологические находки

Друза кристаллов кварца (горный хрусталь),
9см, найден на Урале.
Геологические находки

Геологические находки
Гранаты: Андрадит и Гроссуляр ( найдены в бассейне реки Ахтаранда, Якутия)

История правильных многогранников уходит в глубокую древность. Начиная с 7 века до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.
Историческая справка
Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком
пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.

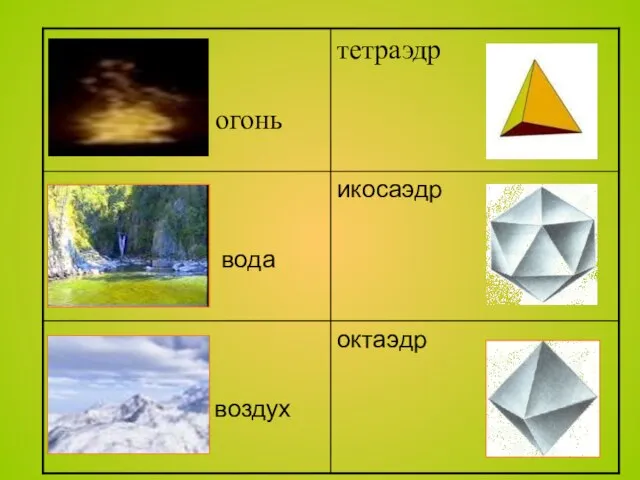
Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды.
Существование пяти правильных многогранников они относили к строению материи и Вселенной.
Согласно этому мнению, атомы основных элементов должны иметь форму различных Платоновых тел:

Все использовали в своих философских теориях
правильные многогранники.
Дальнейшее развитие математики связано с именами
Платона, Евклида, Архимеда, Кеплера

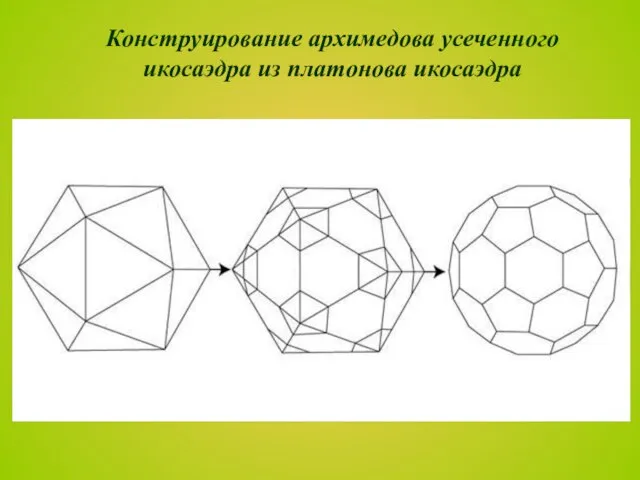
Конструирование архимедова усеченного икосаэдра из платонова икосаэдра

Двойственные многогранники
Куб и октаэдр находятся в положении двойственности друг другу, грани являются q-угольниками, р из которых примыкают к каждой вершине.

Космологическая гипотеза Кеплера
Кеплер попытался связать со свойствами правильных многогранников некоторые свойства Солнечной системы.
Он предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел). Между каждой парой "небесных сфер", по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел. Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна.

Многогранники в искусстве
«Поистине, живопись — наука и законная дочь природы,
ибо она порождена природой»
(Леонардо да Винчи)

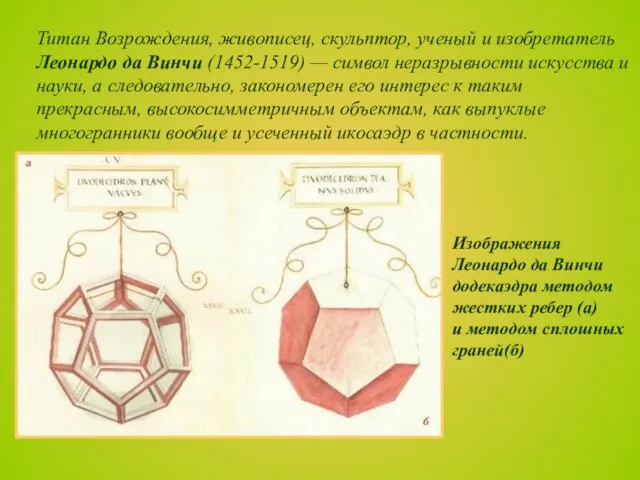
Титан Возрождения, живописец, скульптор, ученый и изобретатель
Леонардо да Винчи (1452-1519) — символ неразрывности искусства и науки, а следовательно, закономерен его интерес к таким прекрасным, высокосимметричным объектам, как выпуклые многогранники вообще и усеченный икосаэдр в частности.
Изображения Леонардо да Винчи
додекаэдра методом жестких ребер (а)
и методом сплошных граней(б)

Знаменитый художник, увлекавшийся геометрией,
Альбрехт Дюрер
(1471- 1528),
в известной гравюре «Меланхолия»
на переднем плане
изобразил додекаэдр.

Правильные геометрические тела - многогранники - имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.
Голландский художник Мориц Корнилис Эшер (1898-1972)создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.
На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

Изящный пример звездчатого додекаэдра можно найти в его работе "Порядок и хаос". В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором.
Наиболее интересная работа Эшера - гравюра "Звезды", на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров.
Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры.

На картине художника Сальвадора Дали «Тайная Вечеря» Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра.
Форму додекаэдра, по мнению древних, имела ВСЕЛЕННАЯ , т.е. они считали, что мы живём внутри свода, имеющего форму поверхности правильного додекаэдра.

Применения икосаэдров
Титульный лист
книги Ж. Кузена
«Книга о перспективе».
Надгробный памятник
в кафедральном соборе Солсбери.

Многогранники в архитектуре
Наука геометрия возникла из практических задач, ее предложения выражают реальные факты и находят многочисленные применения.
Геометрия появляется всюду, где нужна хотя бы малейшая точность в определении формы и размеров.

В III веке до н.э. был построен маяк, чтобы корабли могли благополучно миновать рифы на пути в александрийскую бухту. Ночью им помогало в этом отражение языков пламени, а днем - столб дыма. Это был первый в мире маяк, и простоял он 1500 лет
Фаросский маяк состоял из трех мраморных башен, стоявших на основании из массивных каменных блоков. Первая башня была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню. Верхняя башня формой напоминала цилиндр, в котором горел огонь, помогавший кораблям благополучно достигнуть бухты. На вершине башни стояла статуя Зевса Спасителя. Общая высота маяка составляла 117 метров.
Александрийский маяк

Царская гробница
Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц. Пирамида Хуфу, самая дальняя на рисунке, является самой большой. Пирамида его сына находится в середине и смотрится выше, потому что стоит на более высоком месте.

Многогранники в архитектуре Москвы
Собор непорочного зачатия
Девы Марии
на малой Грузинской
Исторический музей

Казанская церковь в Москве
Многогранники в архитектуре Москвы

ЦУМ
Высотки. Котельники
Многогранники в архитектуре Москвы

Телеграф
Многогранники в архитектуре Москвы

Малый Ржевский пер.
Новоарбатский замок
Многогранники в архитектуре Москвы

ул Пятницкая
Многогранники в архитектуре Москвы

Литература:
- Энциклопедия для детей. Т. 11. Математика. – М: Аванта плюс, 2002.
- Энциклопедия для детей. Я познаю мир.Математика. – М: Издательство АСТ, 1999.
- Ворошилов А.В. Математика и искусство. - М. просвещение, 1992. – 352
- Рыбников К.А. История математики: Учебник. - М.: Изд-во МГУ, 1994. - 495 с