«Определение показателя Херста акций компаний-составляющих индекса Dow Jones››

Показатель Херста
Свой эмпирический закон Хёрст открыл, занимаясь изучением Нила. Впоследствии оказалось, что многие другие природные явления хорошо описываются этим законом. Оказывается, временные последовательности измерений таких величин, как температура, сток рек, количество осадков, толщина колец деревьев или высота морских волн можно исследовать методом нормированного размаха или методом Хёрста. Такие последовательности характеризуются показателем Н, показателем Хёрста.
Временные последовательности, для которых Н больше 0.5, относятся к классу персистентных - сохраняющих имеющуюся тенденцию. Если приращения были положительными в течение некоторого времени в прошлом, то есть происходило увеличение, то и впредь в среднем будет происходить увеличение. Таким образом, для процесса с Н > 0.5 тенденция к увеличению в прошлом означает тенденцию к увеличению в будущем. И наоборот, тенденция к уменьшению в прошлом означает, в среднем, продолжение уменьшения в будущем. Чем больше Н, тем сильнее тенденция.
При Н=0.5 никакой выраженной тенденции процесса не выявлено, и нет оснований считать, что она появится в будущем. Примером такого процесса может быть броуновское движение.
Случай Н < 0.5 характеризуется антиперсистентностью - рост в прошлом означает уменьшение в будущем, а тенденция к уменьшению в прошлом делает вероятным увеличение в будущем. И чем меньше Н, тем больше эта вероятность. В таких процессах после возрастания переменной обычно происходит её уменьшение, а после уменьшения - возрастание.

Метод скалирования временного ряда
Алгоритм
берется временной ряд Sn (к примеру цены закрытий акций в конце торгового дня), из него путем взятия натурального логарифма получаем новый ряд Sn → ln(Sn);
далее считаем логарифмические доходности с разными приращениями, взятыми по степеням двойки δ=2, 4, 8, 16, 32, 64, 128:
Δ1(δ)= ln(Sδ+1)- ln(S1)
Δ2(δ)= ln(Sδ+2)- ln(S2)
…
ΔN(δ) (δ)= ln(Sδ+ N(δ))- ln(S N(δ))
получаем 7 временных рядов Δk(δ) и вычиляем для каждого стандартное отклонение:
После чего строится график log2 от log2 - по полученным точкам с помощью линейной регрессии проводится прямая. Тангенс угла наклона регрессионной прямой к оси Ox и будет значением искомого показателя Херста.

Проверка на искусственных данных
Алгоритм тестировался на временном ряде фрактального броуновского движения, генерируемого специальной функций в Matlab с заранее заданным значением H.
Брались значения длин ряда N от 212 до 215 со значениями H от 0,05 до 0,95 с шагом 0,05. Для каждого подсчитывался H и его отклонение от реального значения ΔH. В результате многократных компьютерных симуляций (N=1000 для каждого значения H) были получены средние значния отклонений вычиляемого алгоритмом показателя от его реального значения

Ошибка алгоритма при различных изначальных значениях H

Подсчет показателя Херста акций компаний Dow Jones

Результаты вычислений для всех 30 компаний-составляющих индекса Dow Jones

DMA
Шаг 1. На первом шаге метод определят тренды в данных используя скользящее среднее. Простое скользящее среднее придает одинаковые веса каждому значению ряда в окне размера n. Позиция, к которой приписывается среднее всех взвешенных данных, определяет относительный вклад «прошлых» и «будущих» отсчетов. Здесь будет рассматриваться отстающее скользящее среднее.
Для окна размера n простое отстающее скользящее среднее определяется как
где y(i) – это интегрированный сигнал, определяемый как y(i)=
u(j)-исходные данные.
Шаг 2. Когда получено скользящее среднее , следующим шагом мы «детрендруем» сигнал, вычитая тренд из :
Для запаздывающего скользящего среднего считаются флуктуации для окна размера n как
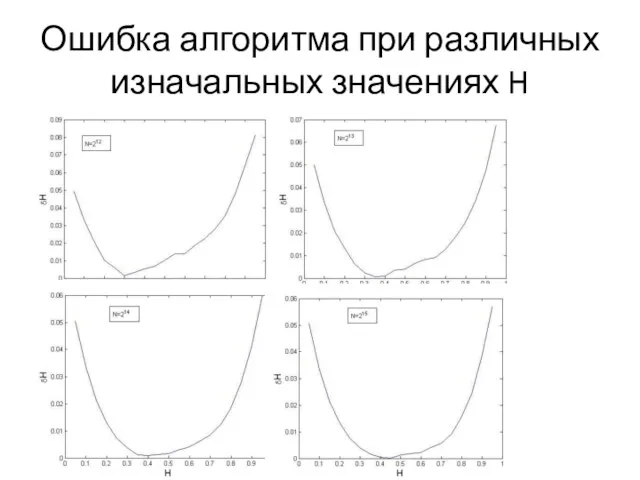
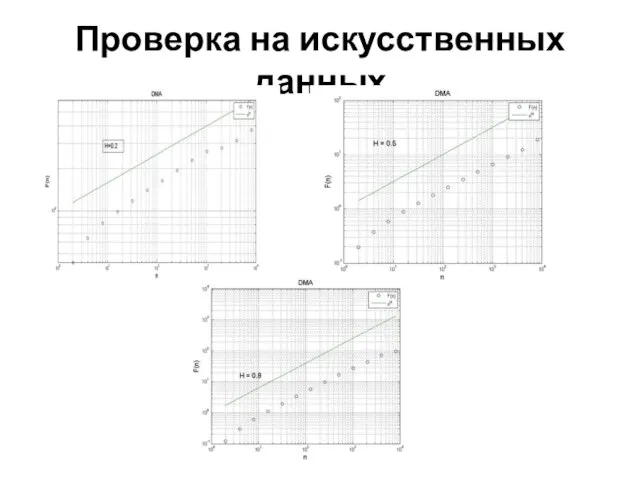
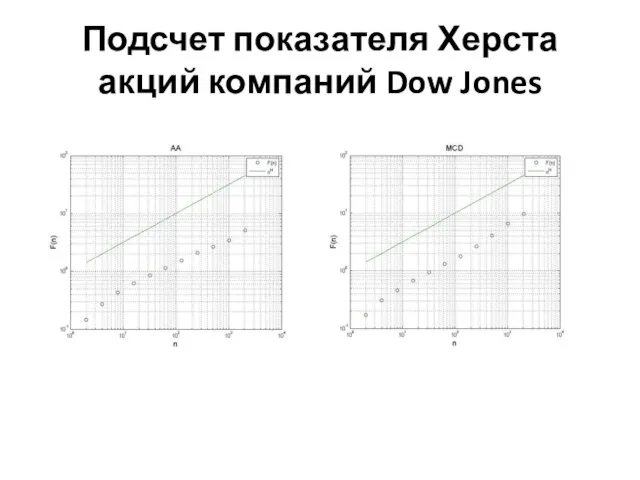
Шаг 3. Повторяя расчет для разных n получим флуктуационную функцию F(n). Степенное отношение между F(n) и размером n указывает на автомодельное поведение.
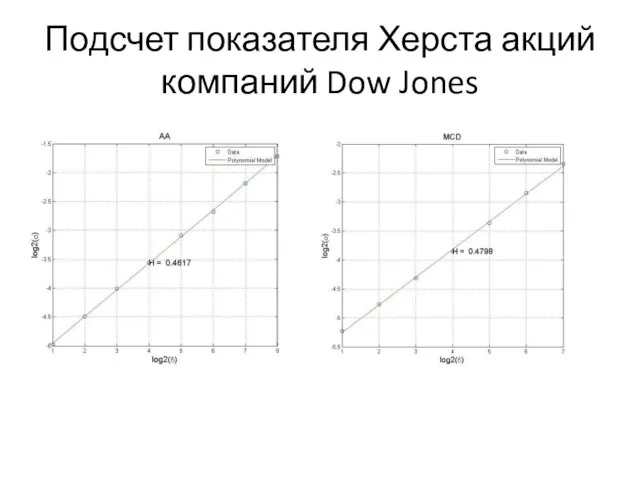
Цель – получить такую зависимость, поскольку показатель степени α и есть искомый показатель Херста.
,

Проверка на искусственных данных

Подсчет показателя Херста акций компаний Dow Jones

Результаты вычислений для всех 30 компаний-составляющих индекса Dow Jones