Содержание
- 2. 1.1. Понятие множества. Логические символы Под множеством понимают совокупность определенных и отличных друг от друга объектов,
- 3. Если множество А состоит из элементов а, b, с, d, то пишут Если множество А задается
- 4. Квантор общности обозначается (“любой”, “всякий”, “каждый”). Выражение “для любого x из множества М” можно записать короче:
- 5. Символ логического следствия (“следует”, “вытекает”). Выражение “из утверждения a следует утверждение b ” записывают так: .
- 6. Множества А и В называются равными, если каждый элемент множества А является элементом множества В и,
- 7. Множество А, называется подмножеством множества В , если каждый элемент множества А является элементом множества В.
- 8. Пусть дано универсальное множество U. Множества А и В - произвольные подмножества множества U. Объединением множеств
- 9. Пересечением множеств А и В называется множество, содержащее из всех тех и только тех элементов, каждый
- 10. Разностью двух множеств А и В называется множество, содержащее из всех тех и только тех элементов,
- 11. Пара элементов называется упорядоченной, если указан порядок записи элементов x и y. Считается, что Элементы x
- 13. 1.3. Отображение множеств. Эквивалентность множеств Пусть А, В произвольные множества и f - закон (правило), по
- 14. Отображение называют взаимно однозначным или биективным, если каждый элемент является образом только одного элемента . Отображение
- 15. Два множества А и В называются эквивалентными (равномощными), если существует хотя бы одно взаимно однозначное отображение
- 17. Скачать презентацию














 Финансовая поддержка субъектов малого и среднего предпринимательства
Финансовая поддержка субъектов малого и среднего предпринимательства Отдел энергоаудита - Спартак
Отдел энергоаудита - Спартак Презентация на тему: Вильфредо Парето
Презентация на тему: Вильфредо Парето Презентация на тему Прекращение уголовного дела и уголовного преследования. Порядок и основания
Презентация на тему Прекращение уголовного дела и уголовного преследования. Порядок и основания  Виды предложений по цели высказывания и по интонации
Виды предложений по цели высказывания и по интонации Тема урока: Актуальные и вечные проблемы в повести В.Г. Распутина «Прощание с Матерой»
Тема урока: Актуальные и вечные проблемы в повести В.Г. Распутина «Прощание с Матерой» Дискурс-анализ в теории перевода
Дискурс-анализ в теории перевода УПРАВЛЕНИЕ МЕТРОЛОГИИ
УПРАВЛЕНИЕ МЕТРОЛОГИИ К.Д.Ушинский - классик педагогики и мой учитель.
К.Д.Ушинский - классик педагогики и мой учитель. V конкурс художественного и декоративно-прикладного творчества Рождество Христово – 2021г
V конкурс художественного и декоративно-прикладного творчества Рождество Христово – 2021г Проблемы молодежи
Проблемы молодежи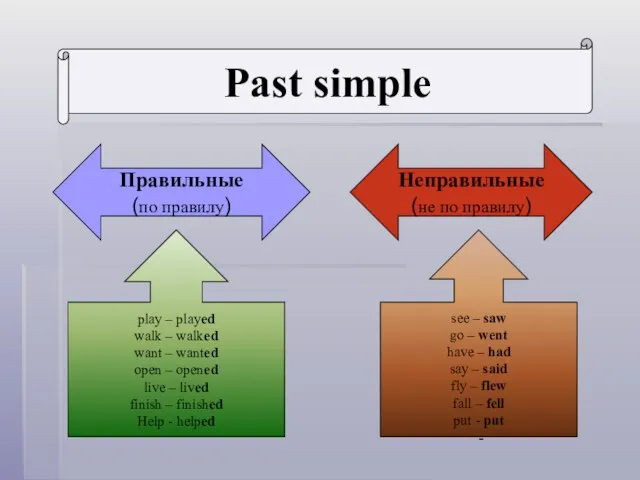 Past simple
Past simple Экзаменационная работа по алгебре
Экзаменационная работа по алгебре Костанайская Епархия
Костанайская Епархия Необходимые условия для обеспечения качественного инклюзивного образования
Необходимые условия для обеспечения качественного инклюзивного образования Презентация классного коллектива 3В классаМОУ «Вурнарская СОШ №2» п.Вурнары Чувашской Республики
Презентация классного коллектива 3В классаМОУ «Вурнарская СОШ №2» п.Вурнары Чувашской Республики Автоматизированная система управления грузовой станцией (АСУ ГС)
Автоматизированная система управления грузовой станцией (АСУ ГС) СССР в 1953-1964 гг
СССР в 1953-1964 гг Притча – источник народной мудрости
Притча – источник народной мудрости Тема+3+Формы+общественного+хозяйства
Тема+3+Формы+общественного+хозяйства Галерея искусств индейцев
Галерея искусств индейцев Выборочное образование. И почему оно необходимо
Выборочное образование. И почему оно необходимо Что изучает физика (7 класс)
Что изучает физика (7 класс) Постная кухня. Посты в православии
Постная кухня. Посты в православии Готовимся к встрече годаЧёрного водяного дракона
Готовимся к встрече годаЧёрного водяного дракона Почему болеют цингой
Почему болеют цингой Сиқырлы тон ертегісі
Сиқырлы тон ертегісі Подчинительная связь слов в словосочетании
Подчинительная связь слов в словосочетании