20141028_ustroystvo_summatora

Содержание
Основные понятия
Полусумматор
Сумматор
Построение схемы последовательного сумматора
Работа сумматора

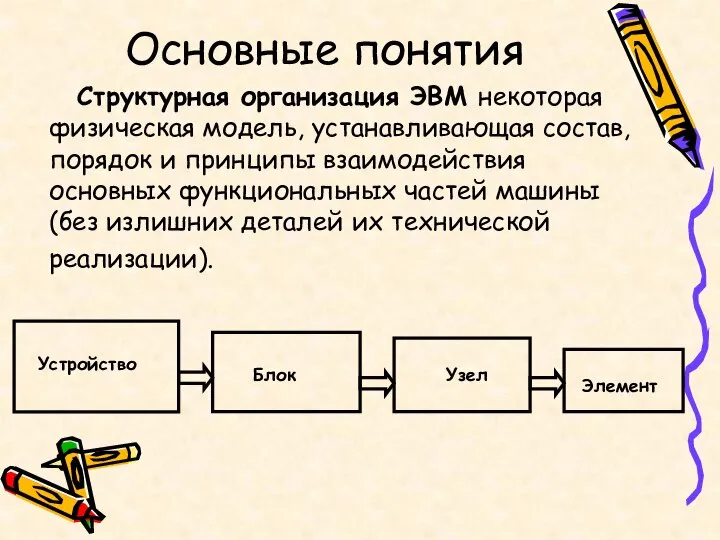
Основные понятия
Структурная организация ЭВМ некоторая физическая модель, устанавливающая состав, порядок и принципы взаимодействия основных функциональных частей машины (без излишних деталей их технической реализации).

Элемент, простейшее устройство ЭВМ, выполняющее одну операцию над входными сигналами (пример – логический элемент).

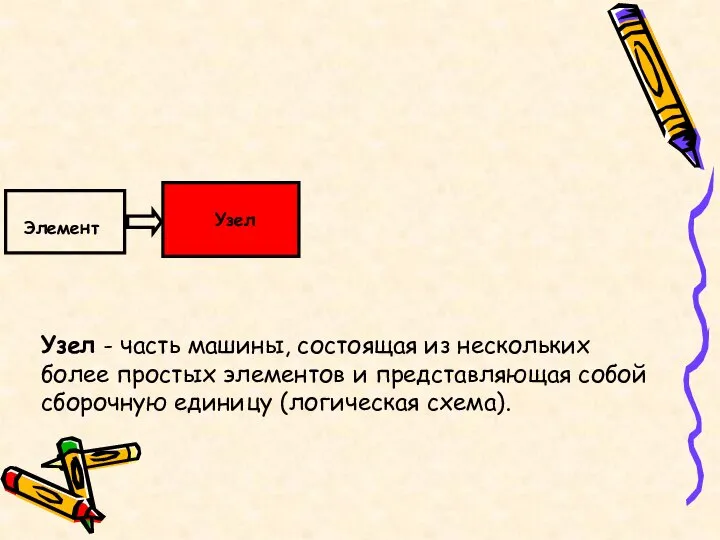
Узел - часть машины, состоящая из нескольких более простых элементов и представляющая собой сборочную единицу (логическая схема).

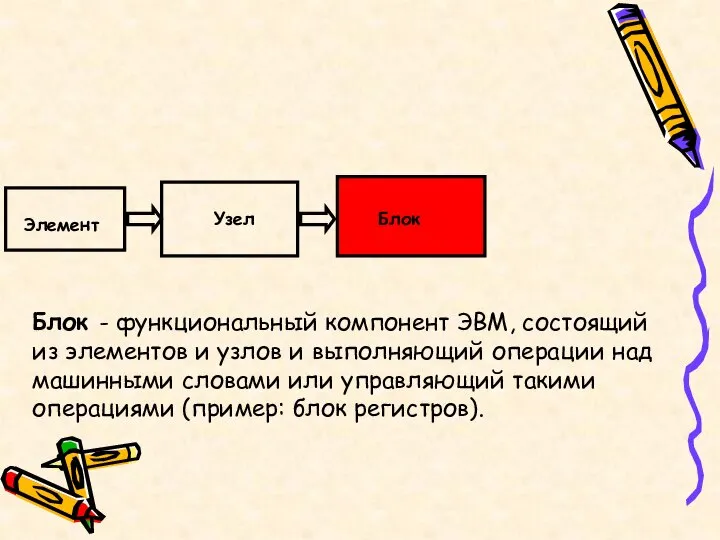
Блок - функциональный компонент ЭВМ, состоящий из элементов и узлов и выполняющий операции над машинными словами или управляющий такими операциями (пример: блок регистров).

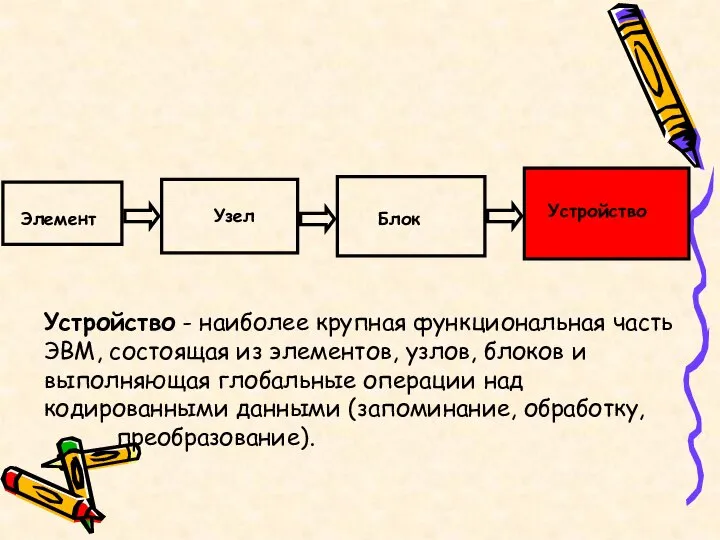
Устройство - наиболее крупная функциональная часть ЭВМ, состоящая из элементов, узлов, блоков и выполняющая глобальные операции над кодированными данными (запоминание, обработку, преобразование).

Узел ЭВМ выполняющий арифметическое суммирование кодов чисел, называется сумматором.

Операция суммирования осуществляется в сумматорах поразрядно с использованием одноразрядных суммирующих схем. При этом в каждом разряде требуется выполнить сложение трех двоичных цифр данного разряда: первого слагаемого Хi, цифры этого же разряда второго слагаемого Yi и цифры переноса Pi из соседнего младшего разряда.
И тогда такое суммирование разбивают на две аналогичные операции: суммирование двух цифр слагаемых и суммирование полученного результата с переносом из соседнего младшего разряда. Каждая из этих операций выполняется схемой, называемой полусумматором.

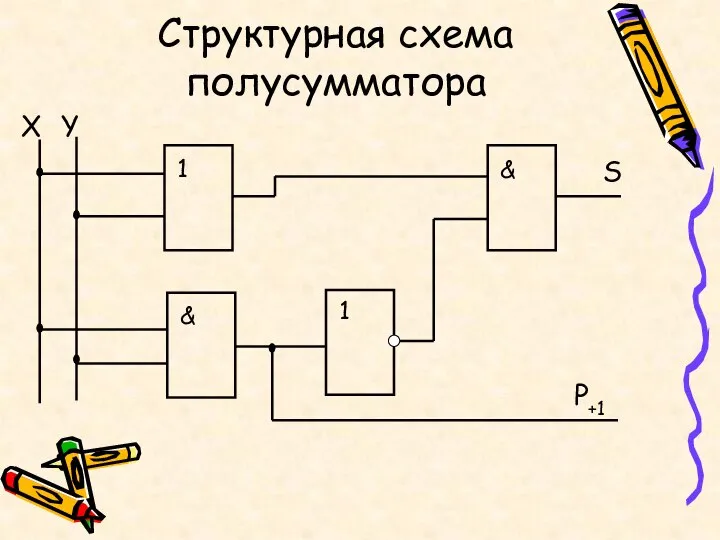
Полусумматор
Рассмотрим таблицу истинности работы полусумматора на два входа X 0 и Y0. Его можно использовать при сложении «0» разрядов. На его выходах образуется сумма S данного разряда и осуществляется перенос Р+1 в следующий старший разряд.

По таблице можно составить логическое выражение для суммы S и переноса Р +1:
P+1 = X&Y

Структурная схема полусумматора

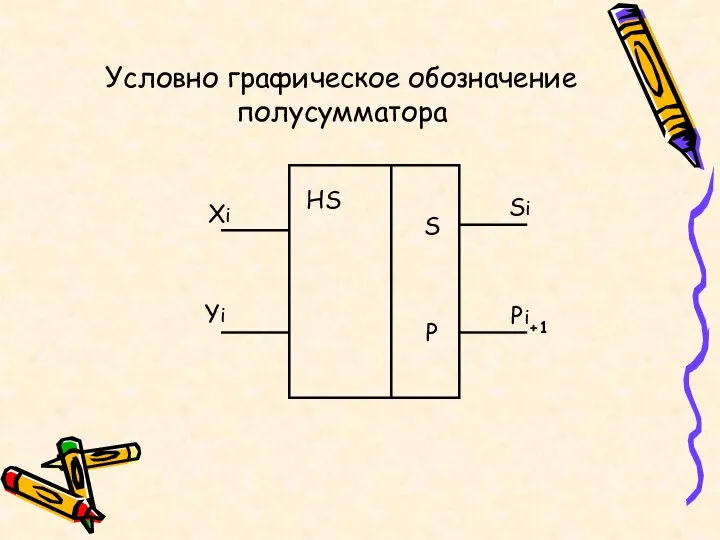
Условно графическое обозначение полусумматора
HS
S
P
Xi
Yi
Si
Pi+1

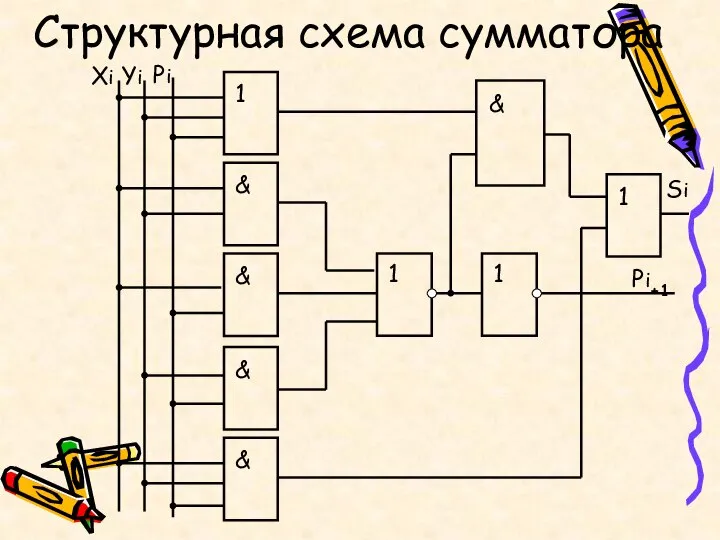
Сумматор
Рассмотрим таблицу истинности сложения цифр в одном из разрядов

Составим минтермы для Si и Pi+1
Целесообразно эти выражения преобразовать так, чтобы в формулах для Si и Pi+1 были по возможности одинаковые члены, что, естественно, сократит количество используемых элементов. Один из вариантов таких преобразований дают выражения:
Pi+1 = Xi&Yi + Xi&Pi + Yi&Pi

Структурная схема сумматора

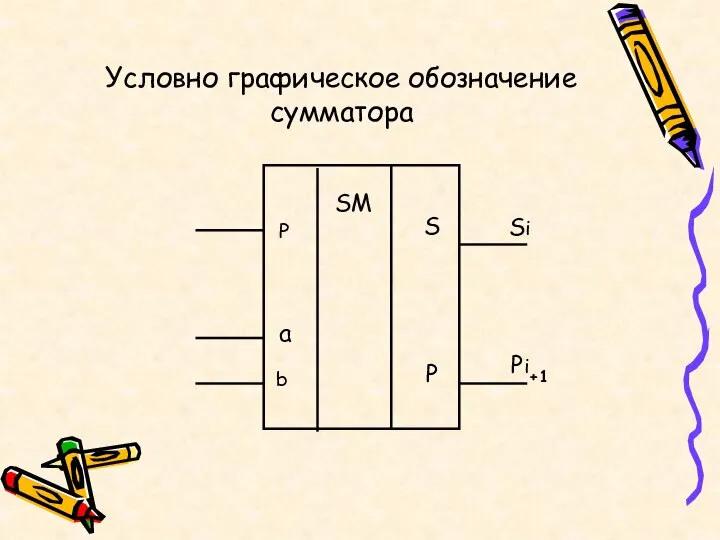
SM
S
P
Si
Pi+1
a
b
P
Условно графическое обозначение сумматора

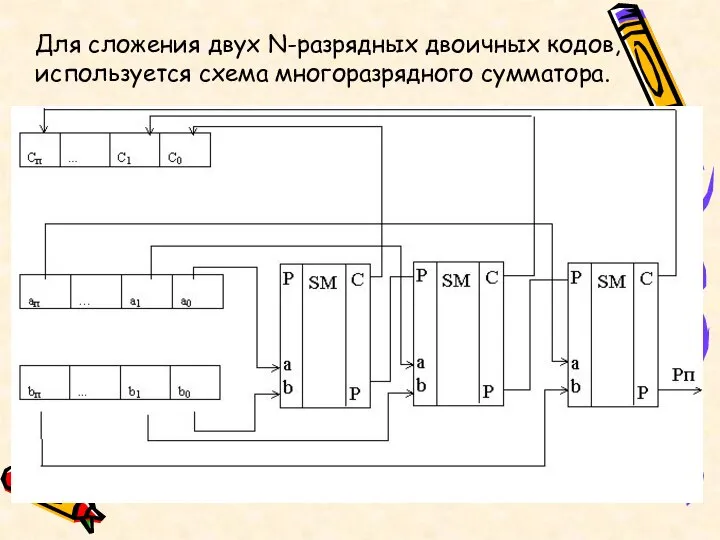
Для сложения двух N-разрядных двоичных кодов, используется схема многоразрядного сумматора.

Работа сумматора
Даны числа 12 и 5.
Построить таблицу истинности и схему полного последовательного сумматора сложения этих чисел.
1. Переводим эти числа в двоичную СС:
3 2 1 0
12-> 1100
2 1 0
5-> 101

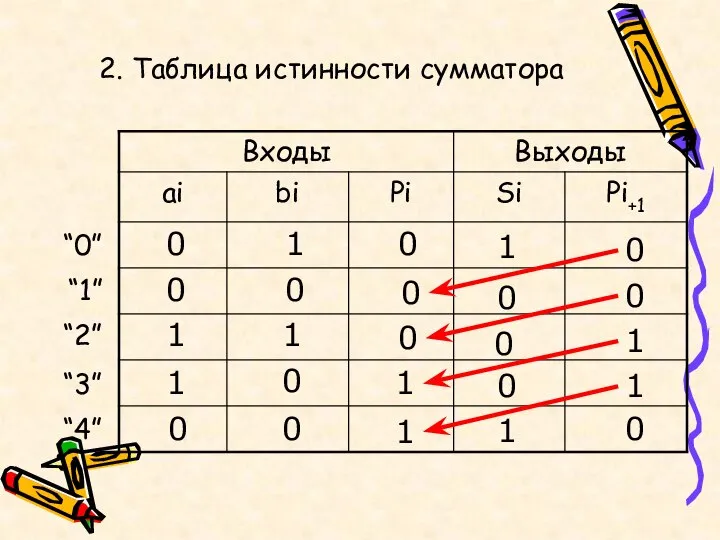
2. Таблица истинности сумматора
0
1
1
0
0
0
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0

Структурная схема сумматора
0