Содержание
- 2. Некоторые утверждения о свойствах геометрических фигур принимаются в качестве исходных положений, на основе которых доказываются далее
- 3. АКСИОМЫ: Через любые две точки проходит прямая, и притом только одна. На любом луче от его
- 4. «аксиома» «аксиос» - ценный, достойный
- 5. АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ
- 6. НИКОЛАЙ ИВАНОВИЧ ЛОБАЧЕВСКИЙ (1792-1856)
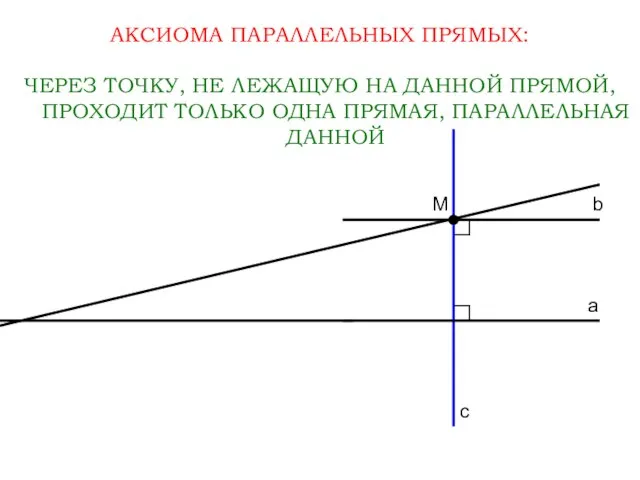
- 7. АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: ЧЕРЕЗ ТОЧКУ, НЕ ЛЕЖАЩУЮ НА ДАННОЙ ПРЯМОЙ, ПРОХОДИТ ТОЛЬКО ОДНА ПРЯМАЯ, ПАРАЛЛЕЛЬНАЯ ДАННОЙ
- 8. УТВЕРЖДЕНИЯ, КОТОРЫЕ ВЫВОДЯТСЯ НЕПОСРЕДСТВЕННО ИЗ АКСИОМ ИЛИ ТЕОРЕМ НАЗЫВАЮТСЯ СЛЕДСТВИЯМИ
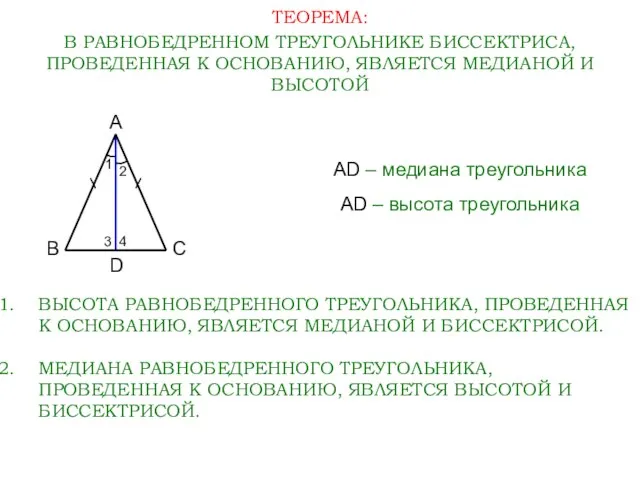
- 9. ТЕОРЕМА: В РАВНОБЕДРЕННОМ ТРЕУГОЛЬНИКЕ БИССЕКТРИСА, ПРОВЕДЕННАЯ К ОСНОВАНИЮ, ЯВЛЯЕТСЯ МЕДИАНОЙ И ВЫСОТОЙ А В С 1
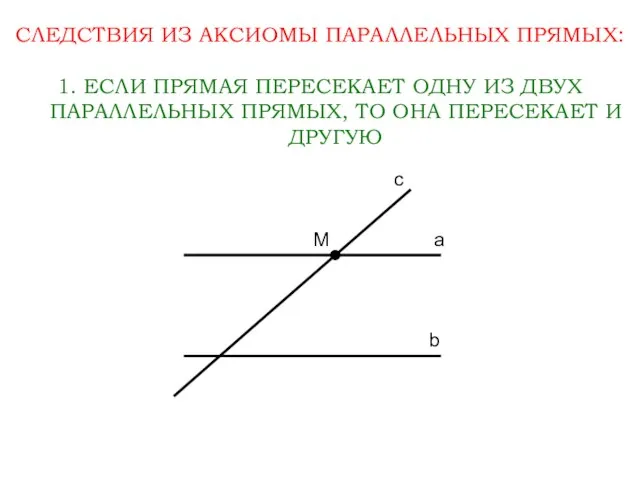
- 10. СЛЕДСТВИЯ ИЗ АКСИОМЫ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: 1. ЕСЛИ ПРЯМАЯ ПЕРЕСЕКАЕТ ОДНУ ИЗ ДВУХ ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ, ТО ОНА
- 12. Скачать презентацию






 Человек и Бог всемогущий
Человек и Бог всемогущий 21 ноября - всемирный день приветствий
21 ноября - всемирный день приветствий Искусство критического реализма во Франции. Гюстав Курбе (1819-1877). Дробильщики
Искусство критического реализма во Франции. Гюстав Курбе (1819-1877). Дробильщики Дослідження сучасних тенденцій
Дослідження сучасних тенденцій Решение задач на расчет количества теплоты
Решение задач на расчет количества теплоты Чистый ручеек нашей речи. Правила общения
Чистый ручеек нашей речи. Правила общения Интернет заплахи
Интернет заплахи Презентация на тему Семья и семейные ценности
Презентация на тему Семья и семейные ценности  Отчет о стажировке в Австрии
Отчет о стажировке в Австрии Урок математики в 6 классе
Урок математики в 6 классе Самые необычные и интересные профессии мира
Самые необычные и интересные профессии мира Рождение фотографии
Рождение фотографии Традиции празднования зимних праздников на Руси
Традиции празднования зимних праздников на Руси 14 декабря – День Наума-Грамотника
14 декабря – День Наума-Грамотника Правила поведения летом
Правила поведения летом Weather. Vocabulary
Weather. Vocabulary Трудные случаи таблицы умножения и деления
Трудные случаи таблицы умножения и деления Geografia_5_klass_23_09_Prezentatsia_k_uroku
Geografia_5_klass_23_09_Prezentatsia_k_uroku Архитектура в Киевской Руси
Архитектура в Киевской Руси Интернет-каталог B2B.by
Интернет-каталог B2B.by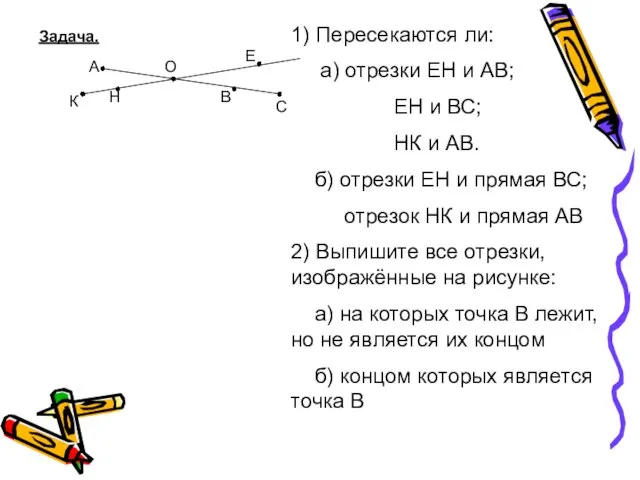 1) Пересекаются ли: а) отрезки ЕН и АВ; ЕН и ВС; НК и АВ. б) отрезки ЕН и прямая ВС; отрезок НК и прямая АВ 2) Выпиш
1) Пересекаются ли: а) отрезки ЕН и АВ; ЕН и ВС; НК и АВ. б) отрезки ЕН и прямая ВС; отрезок НК и прямая АВ 2) Выпиш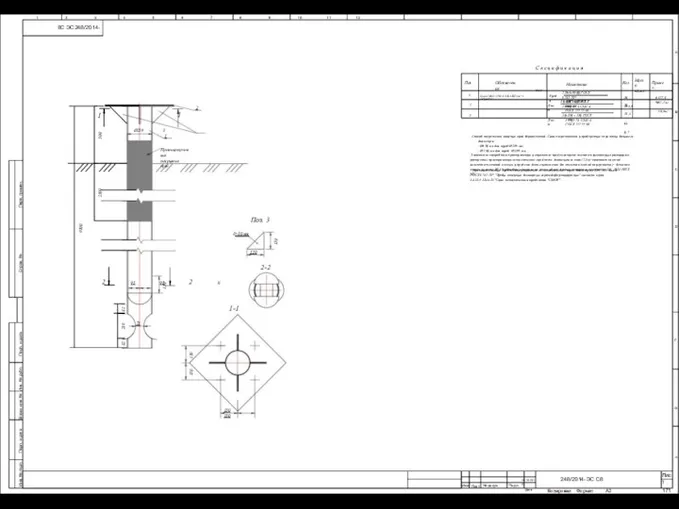 Свая СМОТ с противопучинным покрытием
Свая СМОТ с противопучинным покрытием Дом кольцо
Дом кольцо Псалом 45. Бог прибежище нам и сила, поддержит в скорби, ожидающей нас
Псалом 45. Бог прибежище нам и сила, поддержит в скорби, ожидающей нас Клуб японского языка и культуры. Вводный урок
Клуб японского языка и культуры. Вводный урок Vertex Standard VX-231
Vertex Standard VX-231 Demograficheskaya_situatsia_Brazilii (1)
Demograficheskaya_situatsia_Brazilii (1) Многоточечная видеоконференцсвязь Tandberg.
Многоточечная видеоконференцсвязь Tandberg.