АЛГЕБРА ЛОГИКИ

Алгебра логики (булева алгебра, алгебра высказываний) – это математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют
и преобразовывают логические высказывания.
Система обозначений и правил, применимая ко всевозможным объектам, от чисел до предложений, и позволяющая закодировать высказывания с помощью символов своего языка, а затем манипулировать ими.
Джордж Буль
(1815-1864)

ПРОСТОЕ высказывание
(логическая переменная) -
ни одна его часть сама
не является высказыванием
СЛОЖНОЕ высказывание
(логическая функция)
Состоит из нескольких простых, соединенных между собой с помощью логических операций
это форма мышления, выраженная
повествовательным
предложением, в которой что-либо
утверждается или отрицается
о предметах, их свойствах или отношениях
ВЫСКАЗЫВАНИЕ

Основные операции булевой алгебры
Конъюнкция – И, логическое умножение
Дизъюнкция – ИЛИ, логическое сложение
Отрицание - НЕ
Любое сложное высказывание можно записать
с помощью основных логических операций
И, ИЛИ, НЕ
С помощью логических схем И, ИЛИ, НЕ можно реализовать
любую логическую функцию, описывающую работу
различных устройств компьютера.

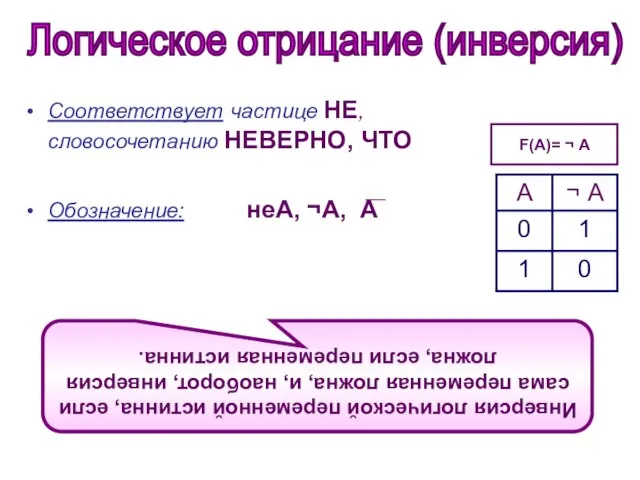
Соответствует частице НЕ, словосочетанию НЕВЕРНО, ЧТО
Обозначение: неА, ¬А, А
F(A)= ¬ А
Логическое отрицание (инверсия)
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.

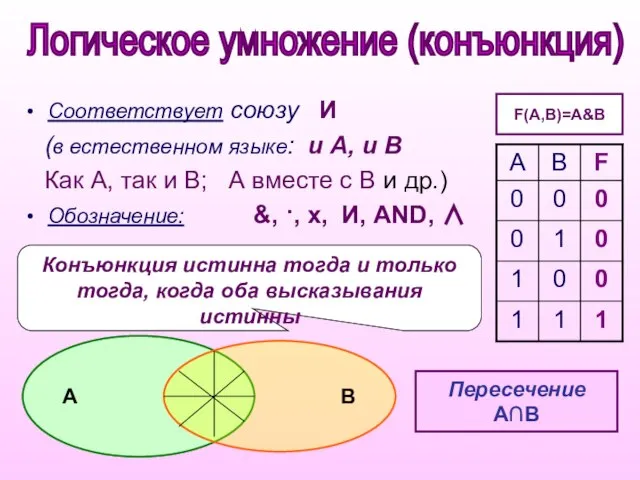
Конъюнкция истинна тогда и только тогда, когда оба высказывания истинны
Соответствует союзу И (в естественном языке: и А, и В
Как А, так и В; А вместе с В и др.)
Обозначение: &, ·, x, И, AND, ∧
F(A,B)=A&B
Пересечение
А∩В
Логическое умножение (конъюнкция)
А
В

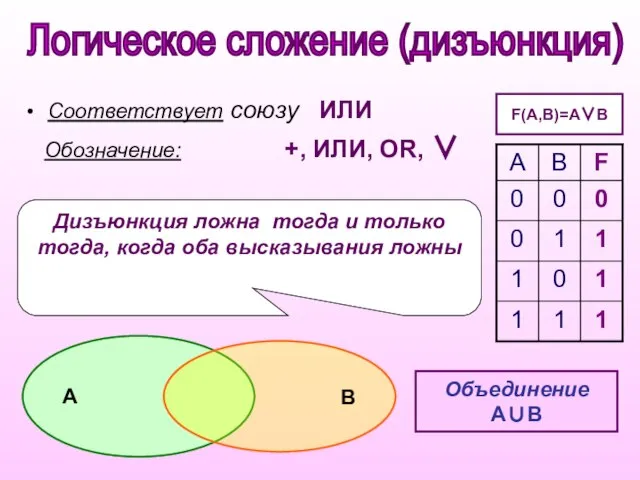
Дизъюнкция ложна тогда и только тогда, когда оба высказывания ложны
Соответствует союзу ИЛИ Обозначение: +, ИЛИ, OR, ∨
F(A,B)=A∨B
Объединение
А∪В
Логическое сложение (дизъюнкция)

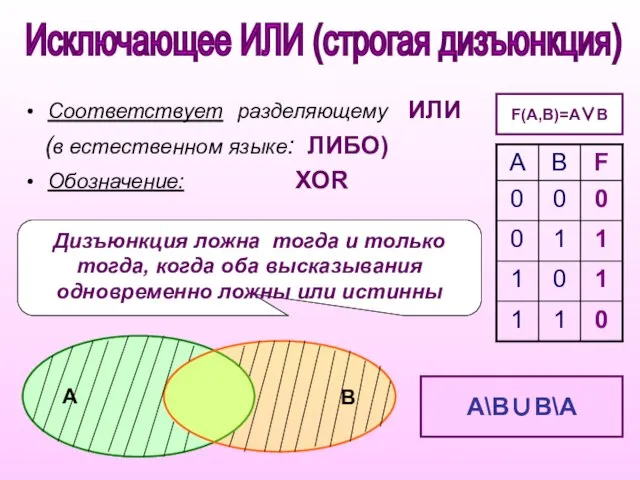
Дизъюнкция ложна тогда и только тогда, когда оба высказывания одновременно ложны или истинны
Соответствует разделяющему ИЛИ
(в естественном языке: ЛИБО)
Обозначение: ХOR
F(A,B)=A∨B
А\В∪В\А
Исключающее ИЛИ (строгая дизъюнкция)

Соответствует речевому обороту ЕСЛИ… ТО
(в естественном языке: если А, то В;
В, если А;
В необходимо для А;
А достаточно для В;
Все А есть В и др.
Обозначение: →, ⇒
F(A,B)=A⇒B
Логическое следование (импликация)
Импликация истинна всегда, за исключением случая, когда А истинно, а В ложно

Соответствует речевым оборотам ЭКВИВАЛЕНТНО;
РАВНОЗНАЧНО,
НЕОБХОДИМО И ДОСТАТОЧНО ДЛЯ;
ТОГДА И ТОЛЬКО ТОГДА, КОГДА
Обозначение: ↔; ≡; ⇔
F(A,B)=A⇒B
Логическое тождество (эквиваленция)
Эквиваленция истинна тогда и только тогда, когда оба высказывания одновременно либо истинны, либо ложны.

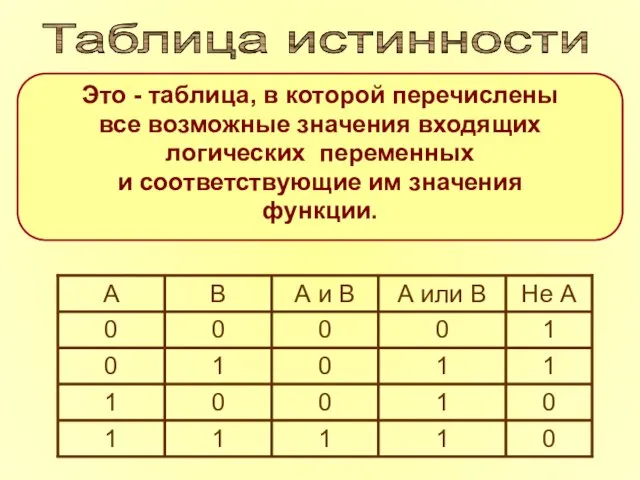
Это - таблица, в которой перечислены
все возможные значения входящих
логических переменных
и соответствующие им значения
функции.
Таблица истинности

Построение таблиц истинности по булеву выражению:
Определить число переменных n.
Определить число строк по формуле q=2n.
3) Записать все возможные значения переменных
4) Определить количество логических операций и их порядок.
5) Количество столбцов в таблице истинности равно числу переменных n плюс количество логических операций.
6) Записать логические операции в таблицу истинности и определить для каждой значение.

1) операция в скобках;
2) отрицание;
3) логическое умножение;
4) логическое сложение;
5) импликация;
6) эквиваленция.
Порядок выполнения логических операций

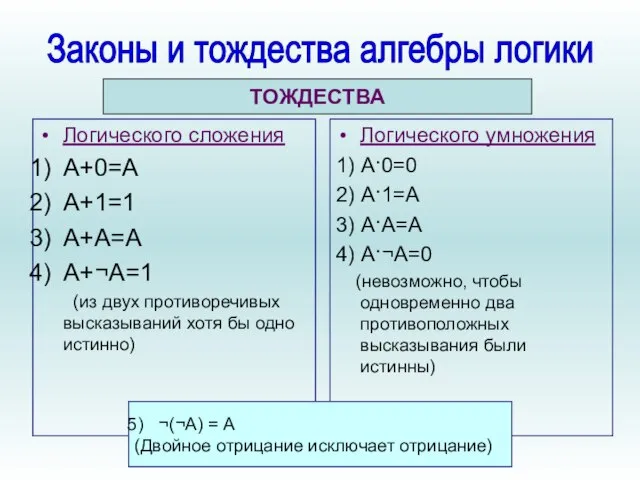
Логического сложения
А+0=А
А+1=1
А+А=А
А+¬А=1
(из двух противоречивых высказываний хотя бы одно истинно)
Логического умножения
1) А·0=0
2) А·1=А
3) А·А=А
4) А·¬А=0
(невозможно, чтобы одновременно два противоположных высказывания были истинны)
Законы и тождества алгебры логики
ТОЖДЕСТВА
¬(¬А) = А
(Двойное отрицание исключает отрицание)

А+В=В+А
2) (А+В)+С=А+(В+С)
3) (А+В)·С=АС+ВС
4) ¬(А+В)=¬А · ¬В
А·В=В·А
2) (А·В)·С=А·(В·С)
3) АВ+С=(А+С)(В+С)
4) ¬(АВ)=¬А+¬В
Законы алгебры логики
А → В = ¬В → ¬А = ¬А + В
6) А⇔В = АВ + ¬(АВ) = (¬А + В)(А + ¬В)
Переместительный закон
Сочетательный закон
Распределительный закон
Закон де Моргана (закон отрицания)

1) 1+А·0
2) Х·Х·1
3) А или (неА и В)
4) F = неХ и (не(неY или Х))
5) F = не(Х и (неХ и неY))
6) А и (А или В) и (В или неВ)
7) (А или В) и (неВ или А) и (неС или В)
Проверь себя
Упростите выражения:

Задача. Даны 3 посылки:
Если Иван – брат Марьи или Иван – сын Марьи, то Иван и Марья – родственники.
Иван и Марья – родственники.
Иван – не сын Марьи.
Можно ли вывести следствие, что «Иван – брат Марьи»?

Вводим обозначения:
А – Иван – брат Марьи.
В – Иван – сын Марьи.
С – Иван и Марья – родственники.
Запишем символически:
А xor В → С
С
¬В
Общая формула:
(((А xor B)→C) and C and ¬B)→A

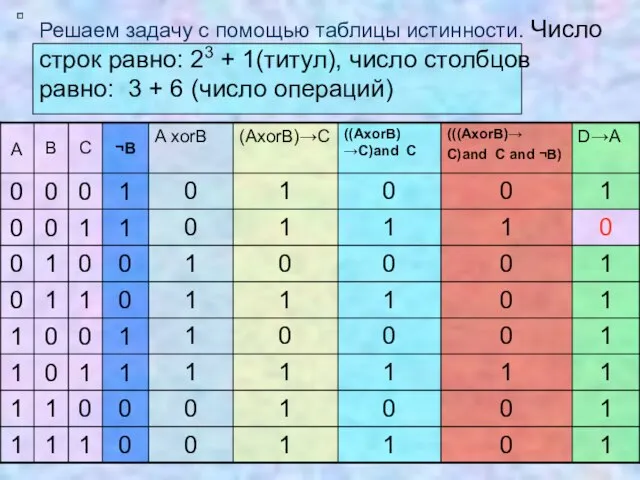
Решаем задачу с помощью таблицы истинности. Число строк равно: 23 + 1(титул), число столбцов равно: 3 + 6 (число операций)

Формула называется тождественно-истинной, если при любых комбинациях значений для входящих в нее переменных принимает значение «истина».
Вывод. Из данных 3-х посылок не следует с необходимостью заключение, что «Иван – брат Марьи». Иван может быть племянником или отцом Марьи, или дядей и т.п.