Алгоритмы

Немного истории
Появление алгоритмов связывают с зарождением математики. В 825 году ученый из города Хорезма Муса аль-Хорезми создал книгу по математике, в которой описал способы выполнения арифметических действий над многозначными числами. Слово «алгоритм» возникло в Европе после перевода на латынь книги этого среднеазиатского математика.

В школьном курсе информатики используется следующее определение:
алгоритм – описание последовательности действий, строгое исполнение которых приводит к решению поставленной задачи за конечное число шагов.

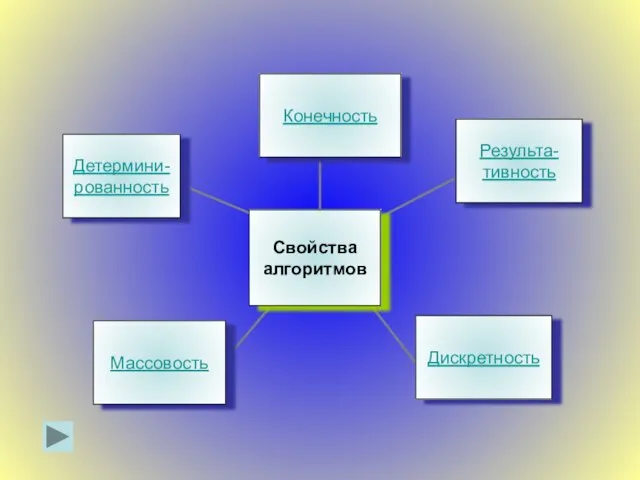
Свойство массовости
показывает, что один и тот же алгоритм можно использовать с разными исходными данными.

Свойство дискретности
указывает, что любой алгоритм должен состоять из конкретных действий, следующих в определенном порядке.

Свойство результативности
требует, чтобы в алгоритме не было ошибок.

Свойство детерминированности
указывает, что любое действие алгоритма должно быть строго и недвусмысленно определено в каждом случае.

Свойство конечности
определяет, что каждое действие в отдельности и алгоритм в целом должны иметь возможность завершения.

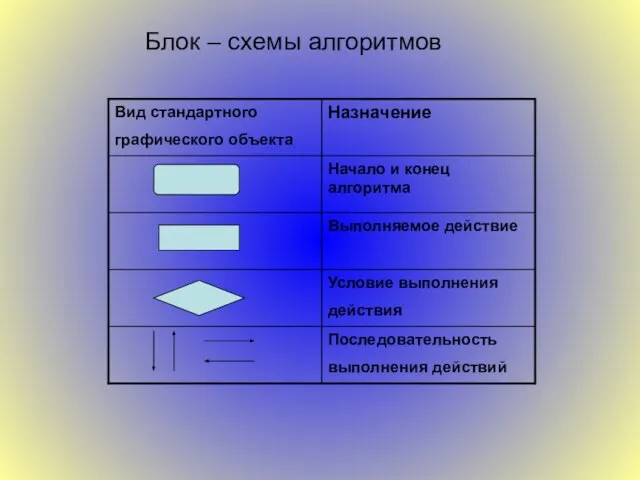
Типовые конструкции алгоритма:
линейная,
циклическая,
разветвляющаяся,
вспомогательная.

Линейный (последовательный) алгоритм
– описание действий, которые
выполняются однократно в
заданном порядке.

Циклический алгоритм
– описание действий, которые
должны повторяться указанное
число раз или пока не
выполнено заданное условие.

Разветвляющийся алгоритм
– алгоритм, в котором в
зависимости от условия
выполняется либо одна, либо
другая последовательность
действий.

Вспомогательный алгоритм
– алгоритм, который можно
использовать в других
алгоритмах, указав только
его имя.

Блок – схемы алгоритмов