Алгоритмы биоинформатики

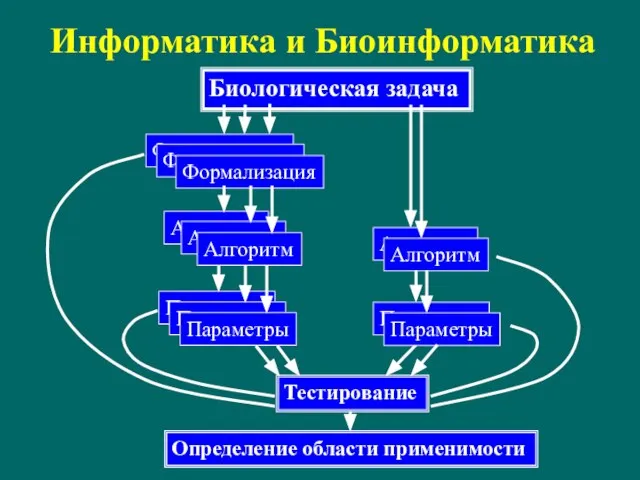
Информатика и Биоинформатика
Биологическая задача
Формализация
Формализация
Формализация
Алгоритм
Алгоритм
Алгоритм
Алгоритм
Алгоритм
Тестирование
Параметры
Параметры
Параметры
Параметры
Параметры
Определение области применимости

Пример: сравнение последовательностей
Тестирование: алгоритм должен распознавать последовательности, для которых известно, что они биологически (структурно и/или функционально) сходны

Сравнение последовательностей
Формализация1: глобальное выравнивание
Алгоритм1: Граф выравнивания, динамическое программирование
Алгоритм1а: Граф выравнивания, динамическое программирование, линейная память
Параметры: Матрица сходства, штраф за делецию

Сравнение последовательностей
Формализация2: локальное выравнивание
Алгоритм2: Граф локального выравнивания, динамическое программирование
Параметры: Матрица сходства, штраф за делецию

Сравнение последовательностей
Формализация3: локальное выравнивание с аффинными штрафами
Алгоритм3: Расширенный граф локального выравнивания, динамическое программирование
Параметры: Матрица сходства, штраф за открытие делеции, штраф за расширение делеции

Сравнение последовательностей
Алгоритм4: FASTA. формальная задача плохо определена
Параметры: Размер якоря, матрица сходства, штраф за делецию

Сравнение последовательностей
Алгоритм5: BLAST. формальная задача плохо определена
Параметры: Размер якоря, матрица сходства, штраф за делецию

Выравнивания

Редакционное расстояние
Элементарное преобразование последовательности: замена буквы или удаление буквы или вставка буквы.
Редакционное расстояние: минимальное количество элементарных преобразований, переводящих одну последовательность в другую.
Формализация задачи сравнения последовательностей: найти редакционное расстояние и набор преобразований, его реализующий

Сколько существует выравниваний?
Дано: две последовательности S1 и S2 длиной m и n. Сколько есть способов написать одну последовательность под другой (со вставками)?
Построим выборочную последовательность S длиной m+n следующим образом: возьмем несколько символов из последовательности S1, потом несколько символов из последовательности S2 потом опять несколько символов из S1, потом опять несколько из S2.
Каждой выборочной последовательности S соответствует выравнивание и по каждому выравниванию можно построить выборочную последовательность. (Доказать!)
Количество выборочных последовательностей равно
Nsel = Cn+mm =(m+n)! / (m!*n!) (Доказать!)
(2n)! 22n
Nalgn = C2nn = ≈ (n!)2 √πn

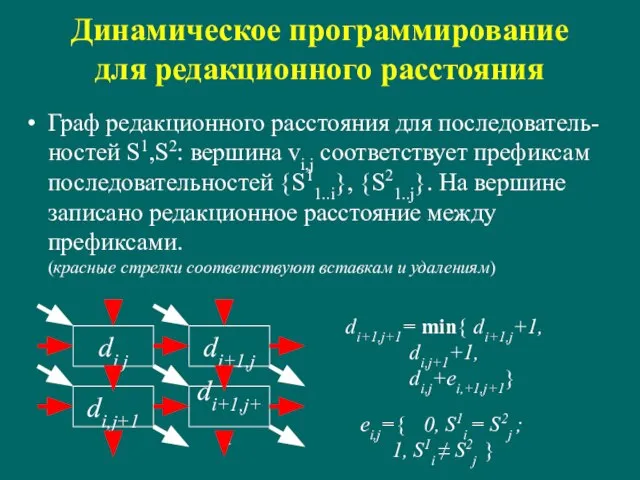
Динамическое программирование для редакционного расстояния
Граф редакционного расстояния для последователь-ностей S1,S2: вершина vi,j соответствует префиксам последовательностей {S11..i}, {S21..j}. На вершине записано редакционное расстояние между префиксами.
(красные стрелки соответствуют вставкам и удалениям)
di,j
di+1,j
di,j+1
di+1,j+1
di+1,j+1= min{ di+1,j+1,
di,j+1+1,
di,j+ei,+1,j+1}
ei,j={ 0, S1i = S2j ;
1, S1i ≠ S2j }

Подмена задачи и обобщение
Заменим расстояния di,j на -di,j. Тогда операцию min надо заменить на max.
Прибавим к -di,j ½ (wi,j= ½ - di,j ), тогда получим функцию сходства: совпадение = ½, замена = -½, делеция = -1.
Функцию сходства W легко обобщить, варьируя штрафы за замену и делеции.
Новая задача: написать одну последовательность под другой так, чтобы максимизировать сходство

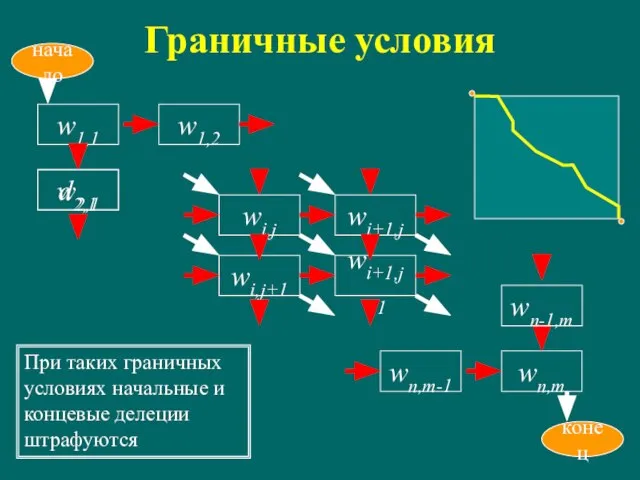
Граничные условия
wi,j
wi+1,j
wi,j+1
wi+1,j+1
w1,1
начало
w1,2
d2,1
wn,m-1
wn,m
w2,1
wn-1,m
конец
При таких граничных условиях начальные и концевые делеции штрафуются

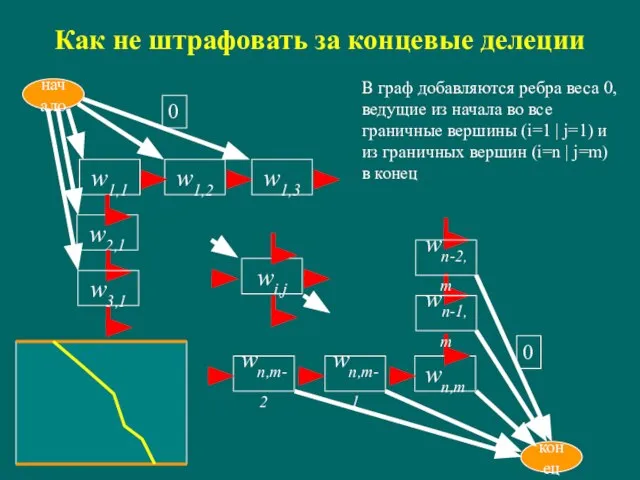
Как не штрафовать за концевые делеции
wi,j
w1,1
начало
w1,2
w2,1
wn,m-1
wn,m
w3,1
wn-1,m
конец
wn,m-2
wn-2,m
w1,3
0
0
В граф добавляются ребра веса 0, ведущие из начала во все граничные вершины (i=1 | j=1) и из граничных вершин (i=n | j=m) в конец

Оценка времени работы и необходимой памяти
Алгоритм посматривает все вершины графа
В каждой вершине делается 3 сравнения
Количество необходимых операций (время работы алгоритма): T=O(n*m). Говорят, что алгоритм выравнивания квадратичен по времени работы.
Для запоминания весов и восстановления оптимального выравнивания надо в каждой вершине запомнить ее вес и направление перехода. Таким образом, алгоритм квадратичен по памяти.

Где можно сэкономить?
Во-первых не обязательно запоминать веса во всех вершинах. При просмотре матрицы выравнивания (графа выравнивания) можно идти по строкам. При этом нам необходима только предыдущая строка.

Линейный по памяти алгоритм Миллера-Маерса
Разбиваем одну из последовательностей на две равные части
Для каждой точки x линии раздела находим веса оптимальных выравниваний из начала в x и из конца в x:
W+(x), W-(x).
Вес оптимального выравнивания, проходящего через точку x равен
W(x)=W+(x) + W-(x).
Вес оптимального выравнивания равен
W = maxx (W(x))
Таким образом, найдена одна точка, чрез которую проходит оптимальное выравнивание за время T=C*n2.
S1
S2
x

Алгоритм Миллера-Маерса
Найденная точка x разбивает матрицу выравнивания на четыре квадранта, два из которых заведомо не содержат оптимального выравнивания
Для двух квадрантов, содержащих оптимальный путь можно применить тот же прием, и запомнить точки x' и x".
Просмотр оставшихся квадрантов требует времени T=C*n2/2 (почему?)
Продолжая процедуру деления пополам найдем все точки, через которые проходит оптимальный путь.
Время работы алгоритма
T=C*n2+C*n2/2+C*n2/4+…=
C*n2(1+1/2+1/4+1/8+…);
T=2C*n2;
S1
S2
Важно, что при просмотре мы не запоминали обратных переходов!

Еще один способ сэкономить время и память
Ясно, что выравнивания D1 и D2 не представляют интереса, поскольку содержат в основном делеции
Разумные выравнивания (A) лежат в полосе
Алгоритм: задаемся шириной полосы w и просматриваем только те вершины графа, что лежат в указанной полосе.
D2
D1
A
w

Локальное выравнивание
Локальным оптимальным выравниванием называется такое оптимальное выравнивание фрагментов последовательностей, при котором любое удлинение или укорочение фрагментов приводит только к уменьшению веса.
Локальному оптимальному выравниванию отвечает путь с наибольшим весом, независимо от того, где он начинается и где кончается.

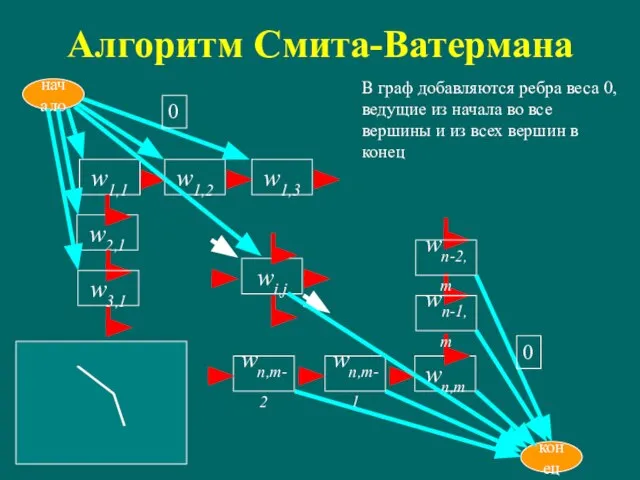
Алгоритм Смита-Ватермана
wi,j
w1,1
начало
w1,2
w2,1
wn,m-1
wn,m
w3,1
wn-1,m
конец
wn,m-2
wn-2,m
w1,3
0
0
В граф добавляются ребра веса 0, ведущие из начала во все вершины и из всех вершин в конец

Алгоритм Смита-Ватермана
Пусть есть какой-то путь с неотрицательными весами
Построим график веса вдоль пути
Абсолютный максимум на этом графике определит точку окончания пути
wmax

Алгоритм Смита-Ватермана
Точка конца пути (от нее начинаем обратный просмотр и восстановление пути) определяется так:
(imax, jmax) = argmax (wi,j)
wi,j = max { wi-i,j-1 + ei,j , i > 1, j > 1
wi-1,j – d , i > 1
wi,j-1 – d , j > 1
0 }
Пусть (при одинаковых параметрах) мы получили вес глобального выравнивания wglob и вес локального выравнивания wloc. Какая величина больше?

Более общая зависимость штрафа за делецию от величины делеции
Простейшая модель делеции: элементарное событие – удаление одного символа. Протяженная делеция – несколько независимых событий удаления одного символа. Работает плохо.
По-видимому более реалистичная модель делеция нескольких символов происходит за одно элементарное событие, а размер делеции является некоторой случайной величиной. Поэтому в качестве штрафа хорошо бы взять что-нибудь вроде
Δ ( l ) = a log( l + 1 ), где l – длина делеции
В любом случае функция Δ ( l ) должна быть выпуклой – должно выполняться неравенство треугольника:
Δ ( l 1+ l2) ≤ Δ ( l 1) + Δ ( l 2)

Более общая зависимость штрафа за делецию от величины делеции. Алгоритм.
Теперь надо просматривать все возможные варианты делеций. Поэтому в каждую вершину входит не 3 ребра, а примерно (n+m)/2 ребер, где n,m – длины последовательностей
Поэтому время работы алгоритма становится кубичным:
T = O ( nm (n+m) );

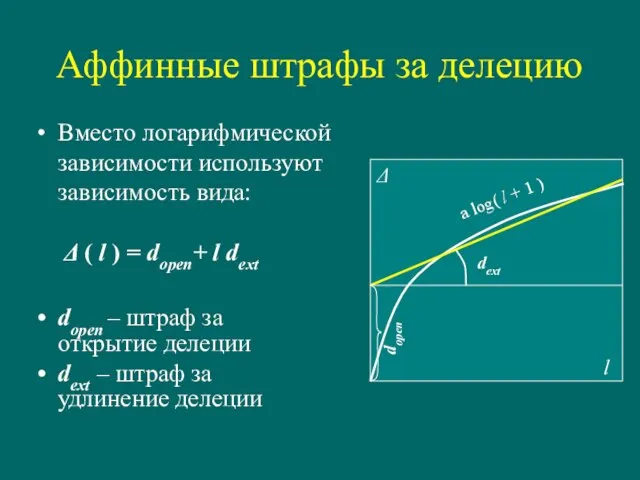
Аффинные штрафы за делецию
Вместо логарифмической зависимости используют зависимость вида:
Δ ( l ) = dopen+ l dext
dopen – штраф за открытие делеции
dext – штраф за удлинение делеции
Δ
l
dopen
dext
a log( l + 1 )

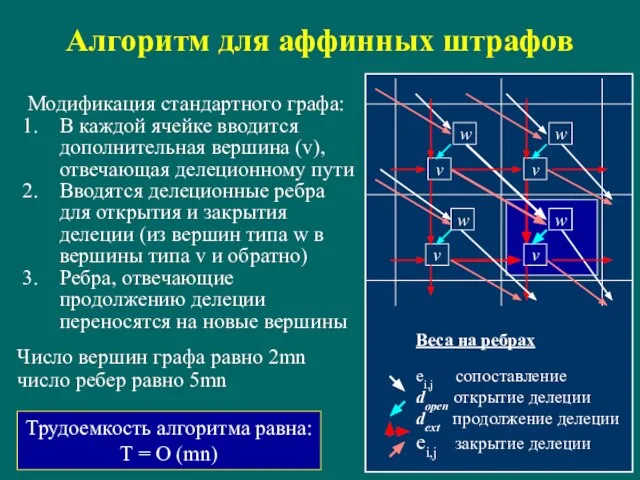
Алгоритм для аффинных штрафов
Веса на ребрах
ei,j сопоставление
dopen открытие делеции
dext продолжение делеции
ei,j закрытие делеции
Модификация стандартного графа:
В каждой ячейке вводится дополнительная вершина (v), отвечающая делеционному пути
Вводятся делеционные ребра для открытия и закрытия делеции (из вершин типа w в вершины типа v и обратно)
Ребра, отвечающие продолжению делеции переносятся на новые вершины
Число вершин графа равно 2mn
число ребер равно 5mn
Трудоемкость алгоритма равна:
T = O (mn)

Рекурсия для аффинных штрафов
w i, j = max ( w i-1, j-1+ei j , v i-1, j-1+ei j , 0 );
v i, j = max ( w i, j – d open , v i-1, j – d ext ,
v i ,j-1 – d ext );
(imax, jmax) = argmax (wi,j)

Матрицы замен

Откуда берутся параметры для выравнивания?
Пусть у нас есть выравнивание. Если последовательности случайные и независимые (модель R), то вероятность увидеть букву α против β
p(α, β | R) = p(α) p(β)
а вероятность выравнивания (x,y) будет равна
p(x,y | R) = Π p(xi) Π p(yi)
Если выравнивание не случайно (модель M), то
p(x,y | M) = Π p(xi , yi)
Отношение правдоподобия:
p(x,y | M) Π p(xi , yi )
=
p(x,y | R) Π p(xi) Π p(yi)
Логарифмируя, получаем
log( p(x,y|M)/p(x,y|R) ) = ∑s(xi,yi);
Матрица замен: s(α, β) = log(pα β /pα pβ)

Серия матриц BLOSUM
База данных BLOCKS (Henikoff & Henikoff) – безделеционные фрагменты множественных выравниваний (выравнивания получены экспертом).
В каждом блоке отбираем подмножество последовательностей, имеющих процент идентичных аминокислот не больше заданного значения ID.
В урезанном блоке в каждой колонке подсчитываем число пар аминокислот
n blcol (α, β)
Усредняем по всем колонкам и по всем блокам:
f (α, β) = ∑ n blcol (α, β) / N col
Элемент матрицы BLOSUMID:
BLOSUM ID (α, β) = log( f (α, β) / f (α) f ( β) )

Серия матриц PAM
Point Accepted Mutation – эволюционное расстояние, при котором произошла одна замена на 100 остатков.
Эволюционный процесс можно представить как Марковский процесс. Если в начальный момент времени t=0 в некоторой позиции был остаток α, то через время Δt в этой позиции с некоторой вероятностью будет остаток β:
p(β| α, Δt) = M Δt(β, α)
M Δ – эволюционная матрица
Через время 2•Δt
p(β| α, 2•Δt) = ∑ γ M Δt(β, γ)• M Δt(γ, α) = M Δt 2(β, α)
Через время N•Δt
p(β| α, N•Δt)= M Δt N(β, α)

Серия матриц PAM
Находим выравнивания, отвечающие расстоянию PAM1
Находим частоты пар и вычисляем частоты пар:
p(αβ) = p(α → β) p(α)+ p(β → α) p(β)
полагая p(α → β) = p(β → α) получаем
p(α → β) = p(αβ) / (p(α)+ p(β))
p(α → α) = 1 – ∑ β≠α p(α → β)
PAMN(αβ) = log (p (α → β)N / pαpβ )

Статистика выравниваний

Параметры выравнивания
В простейшем случае есть три параметра:
премия за совпадение (match)
штраф за несовпадение (mism)
штраф за делецию (indel)
Если все параметры умножить на одну и ту же положительную величину, то само оптимальное выравнивание не изменится, а вес выравнивания умножится на ту же величину
Поэтому можно положить match=1.
Если mism > 2 * indel, то выравнивание не будет иметь замен. (почему?)

Статистика выравниваний
Допустим мы выровняли две последовательности длиной 100 и получили вес 20. Что это значит? Может быть при выравнивании двух случайных последовательностей будет тот же вес?
А что такое случайные последовательности?

Статистика выравниваний
Базовая (вообще говоря неправильная) модель – Бернуллиевские последовательности (символы генерируются независимо друг от друга с заданной вероятностью). Для этой модели математика проще и проще получить оценки
Уточненная модель (лучше, но тоже неправильная) – Марковская цепь (вероятность появления следующего символа зависит от нескольких предыдущих символов). Математика значительно сложнее. Почти ничего не известно.

Частные случаи локального выравнивания
mism = 0, indel = 0 – максимальная общая подпоследовательность
mism = ∞, indel = ∞ – максимальное общее подслово

Наибольшая общая подпоследовательность
Длина оптимальной подпоследовательности есть случайная величина r(n), зависящая от длины последовательностей.
Пусть две последовательности длиной n разбиты на два фрагмента длиной n1 и n2 (n1+n2=n)
Ясно, что оптимальная подпоследовательность будет не хуже, чем объединение оптимальных подпоследовательностей для фрагментов:
r(n) ≥ r1(n1)+r2(n2) (попробуйте понять смысл неравенства)
Отсюда следует, что математическое ожидание
M(r(n)) ≥ M(r(n1)) + M(r(n2)), или M(r(n)) ≥ c •n
Можно показать, что
M(r(n)) – M(r(n1)) + M(r(n2) → 0
Поэтому:
r(n)
r1(n1)
r2(n2)
M(r(n)) ≈ c • n, (n → ∞)

Наибольшее общее слово
Наложим одну последовательность на другую. Будем идти вдоль пары последовательностей и, если буквы совпали, то будем считать успехом, иначе – неудача. Имеем классическую схему испытаний Бернулли. Наибольшему общему слову при таких испытаниях будет соответствовать максимальная серия успехов. Известно, что средняя величина максимальной серии успехов равна:
M(l) = log1/p(n)
Возможных наложений много (порядка длины последовательности). Максимальное общее слово есть максимум от максимальных серий успехов при всех возможных наложениях. Показано (Waterman), что:
M(l) ≈ log1/p(nm) + log1/p(1-p) + γ • log(e) – ½ =
log1/p(Knm), (m,n → ∞, γ ≈ 0.577)
σ(l) ≈ [ π log1/p(e) ]2 / 6 + ½, (не зависит от l !)

Зависимость от параметров
Показано, что зависимость ожидаемого веса выравнивания от длины последовательности может быть либо логарифмической либо линейной в зависимости от параметров. Все пространство параметров разбивается некой поверхностью на две области поведения.
При безделеционном выравнивании поведение логарифмическое, если мат.ожидание веса двух случайных сегментов отрицательно.

Распределение экстремальных значений
Пусть вес выравнивания x (случайная величина) имеет распределение
G(S) = P(x < S)
Тогда при N независимых испытаниях распределение максимального значения будет
GN(x) = GN(x);
Можно показать, что для нормально распределенного G(x)
GN(x) ≈ exp(-KN e λ(x-μ))

e-value & p-value
Количество независимых локальных выравниваний с весом >S описывается распределением Пуассона (Karlin &Altschul) :
E(S) = Kmn e –λS
где λ – положительный корень уравнения
∑ pαpβ e λs(αβ) = 1, s(αβ) – матрица замен
K – константа, зависящая от pα и s(αβ).
e-value: E(S) – ожидаемое количество выравниваний с заданным весом
p-value: p(x>S) = 1- e –E(S) – Вероятность встретить выравнивание с таким или большим весом

Поиск по банку

Поиск по банку. Хеширование.
Подготовка банка – построение хэш-таблицы. Хэш-функция – номер слова заданного размера (l-tuple,
l-грамма).
В хэш-таблице хранятся списки ссылок на последовательности и на позиции в последовательностях, где встречается соответствующая l-грамма.
При поиске запроса (query) в последовательности запроса последовательно находятся l-граммы, далее, по хэш-таблице для них находятся соответствующие документы и позиции.
Пара совпадающих l-грамм в запросе и в банке называется затравкой, якорем, seed.

Поиск по банку. FASTA.
Используется техника поиска якорей с помощью хэш-таблицы.
Два якоря (i1,j1), (i2,j2) принадлежат одной диагонали, если i1 – j1 = i2 – j2
Мощностью диагонали называется количество якорей, принадлежащих диагонали. Иногда в мощность диагонали включают мощности соседних диагоналей (чтобы учесть возможность делеций)
Отбираем n* (n*=10) самых мощных диагоналей и для них пытаемся построить цепочки якорей, или строим S-W выравнивание в полосе
(Wilbur-Lipman-Pearson)
Для оценки стат.значимости используют z-score

Поиск по банку. BLAST1.
Ищем якоря с помощью хэш-таблицы
Каждый якорь расширяем с тем, чтобы получить сегмент совпадения наибольшего веса (HSP – high scoring pair).
Оцениваем его статистическую значимость, и, если она больше порога, то репортируем
Для оценки значимости используется формула Альтшуля
(Altschul, Lipman, Pearson)

Поиск по банку. BLAST2.
T-соседней l-граммой LT для l-граммы L называется такая l-грамма, что вес ее сравнения с L не меньше заданного T:
∑s(Li, LiT) ≥ T
Для аминокислотных последовательностей при просмотре запроса формируем не только те l-граммы, которые встретились в нем, но также все T-соседние l-граммы. Характерное количество l-грамм для белка длиной 300 остатков – 15000.
Расширяются только те якоря, которые принадлежат мощной диагонали (как в FASTA), причем мощность диагонали должна быть ≥ 2T
При расширении диагонали допускается небольшое количество делеций

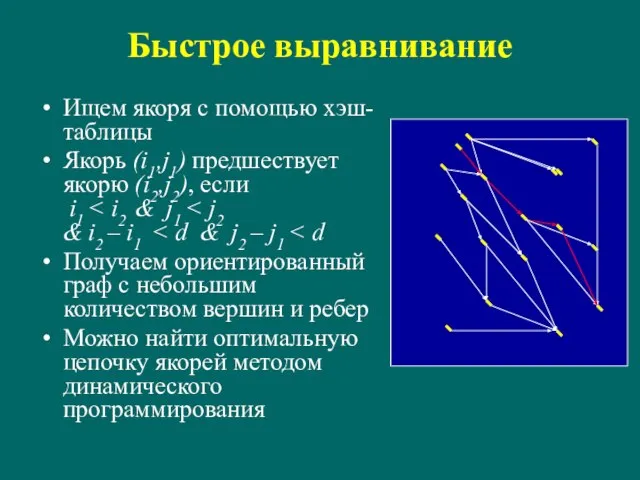
Быстрое выравнивание
Ищем якоря с помощью хэш-таблицы
Якорь (i1,j1) предшествует якорю (i2,j2), если
i1 < i2 & j1 < j2
& i2 – i1 < d & j2 – j1 < d
Получаем ориентированный граф с небольшим количеством вершин и ребер
Можно найти оптимальную цепочку якорей методом динамического программирования

Введение в Байесову статистику

Введение в Байесову статистику
Задача. Мы 3 раза бросили монету и 3 раза выпал орел. Какова вероятность выпадения орла у этой монеты?
Если мы уверены, что монета не кривая, то p = ½
Допустим, что мы взяли монету из мешка, а в мешке монеты разной кривизны. Но при этом мы знаем как распределена кривизна монет Pa(p) (априорное распределение).
Мы хотим на основе наблюдения 3о и априорного распределения распределений вероятностей оценить вероятность выпадения орла у данной монеты.

Введение в Байесову статистику
P(3o | p) = p3;
P(3o, p) = P(3o | p) Pa (p) = P(p | 3o) P(3o);
P(p | 3o)= {P(3o | p) Pa(p)} / P(3o);
Загадочный объект P(3o) – безусловная вероятность трех орлов. Определяется из условия нормировки: ∫ P(p | 3o) = 1;
Окончательно, распределение вероятностей вероятности орла будет:
P(p | 3o)= p3 Pa(p) / ∫ p3 Pa(p) ;

Введение в Байесову статистику
P(p | 3o)= p3 Pa(p) / ∫ p3 Pa(p) dp;
В качестве оценки для искомой вероятности удобно иметь число, а не распределение:
Максимальное значение
pML=argmax p ( P(3o | p)) – максимальное правдоподобие (max likelihood, ML)
Среднее значение
pE=E( P( p | 3o))= ∫ p P( p | 3o) dp;

Введение в Байесову статистику
ML Оценка:
p ML= argmax (p3) = 1;
(не зависит от распределения Pa)
E оценка (матожидание апостериорной вероятности)
pE = ∫ p 4 Pa(p) dp / ∫ p3 Pa(p) dp;
Если мы уверены, что монета правильная, то
Pa (p)=δ(p – ½); pE = ½ ;
Если мы ничего не знаем о распределении Pa (p), то положим Pa (p) = const. Тогда
pE = ∫ p 4 Pa(p) dp / ∫ p3 Pa(p) dp = ¼ / ⅓ = ¾ ;
В более общем случае
pE(no) = (n+1)/(n+2);
MAP оценка (максимум апостериорной вероятности)
pMAP = argmax { P(p | 3o)};

Определения
Пусть у нас есть несколько источников Y событий X (например, несколько монет). Тогда :
P(X | Y) – условная вероятность
P(X,Y) = P(X | Y) P(Y) – совместная вероятность
P(X) = ∑ Y P(X,Y) = ∑ Y P(X |Y) P(Y) – полная вероятность
P(Y | X) – апостериорная вероятность выбора источника (правдоподобие гипотезы)
P(Y) – априорная вероятность выбора источника
Теорема Байеса:
P(X | Y)= P(Y | X) P(X) / P(Y)

Пример
Пусть есть две кости – правильная и кривая (с вероятностью выпасть 6 – 0.5). И пусть нам подсовывают кривую кость с вероятностью 1%. Мы бросили кость 3 раза и 3 раза получили 6. Какова вероятность того, что нам дали кривую кость?
P(кривая кость | 3 шестерки) =
P(3 шестерки | кривая кость) • P(кривая кость)
P(3 шестерки)
P(3 шестерки)=P(3 шестерки | кривая кость) • P(кривая кость) +
P(3 шестерки | правильная кость) • P(правильная кость) = 0.53 • 0.01 + (1/6)3 •0.99 = 0.00125+0.0046 = 0.00585
P(кривая кость | 3 шестерки) = 0.00125/0.00585=0.21
Вывод – кость скорее правильная!

Оценка параметров по результатам
Пусть у нас есть наблюдение D и некоторый набор параметров распределения θ, которые мы хотим оценить (см. пример про 3 орла). Кроме того, у нас есть представление о том, как эти параметры распределены (prior)
Апостериорное распределение вероятностей параметров получаем из теоремы Байеса:
P(θ) P(D |θ)
P(θ | D) =
∫θ P(θ') P(D |θ')

Распределение Дирихле
Определение:
D(θ|α)=Z-1∏ θi αi δ(∑ θi – 1);
Z – нормировочный множитель
αi – параметры распределения
θi ≥ 0 – область определения распределения
δ – дельта-функция (δ(x)=0, x≠0; ∫ δ(x)dx=1;)
θ1
θ2
θ3
Симплекс
Задача: найти объем симплекса в n-мерном пространстве

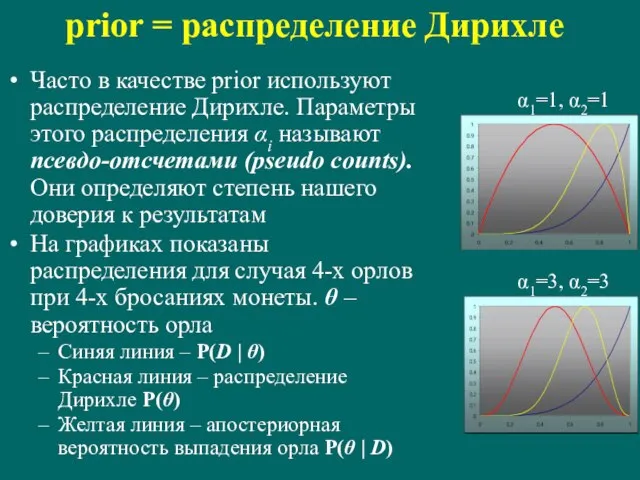
prior = распределение Дирихле
Часто в качестве prior используют распределение Дирихле. Параметры этого распределения αi называют псевдо-отсчетами (pseudo counts). Они определяют степень нашего доверия к результатам
На графиках показаны распределения для случая 4-х орлов при 4-х бросаниях монеты. θ – вероятность орла
Синяя линия – P(D | θ)
Красная линия – распределение Дирихле P(θ)
Желтая линия – апостериорная вероятность выпадения орла P(θ | D)
α1=1, α2=1
α1=3, α2=3

Скрытые Марковские модели (HMM)

Пример
Пусть некто имеет две монеты – правильную и кривую. Он бросает монету и сообщает нам серию результатов. С некоторой вероятностью он может подменить монету. Моменты подмены монеты нам неизвестны, но известно:
результаты бросков
вероятность с которой он заменяет монету
степень кривизны каждой монеты
Задача: определить моменты смены монеты

Биологические примеры
Дана аминокислотная последовательность трансмембранного белка. Известно, что частоты встречаемости аминокислот в трансмембранных и в растворимых частях белка различаются (аналог разных монет). Определить по последовательности где находятся трансмембранные участки.
Дана геномная последовательность. Статистические свойства кодирующих областей отличаются от свойств некодирующих областей. Найти кодирующие области.
• • •
• • •
• • •

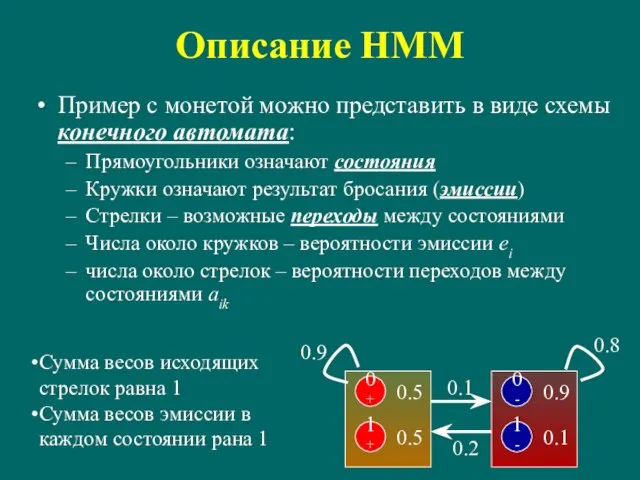
Описание HMM
Пример с монетой можно представить в виде схемы конечного автомата:
Прямоугольники означают состояния
Кружки означают результат бросания (эмиссии)
Стрелки – возможные переходы между состояниями
Числа около кружков – вероятности эмиссии ei
числа около стрелок – вероятности переходов между состояниями aik
0+
1+
0.5
0.5
0-
1-
0.9
0.1
0.9
0.1
0.8
0.2
Сумма весов исходящих стрелок равна 1
Сумма весов эмиссии в каждом состоянии рана 1

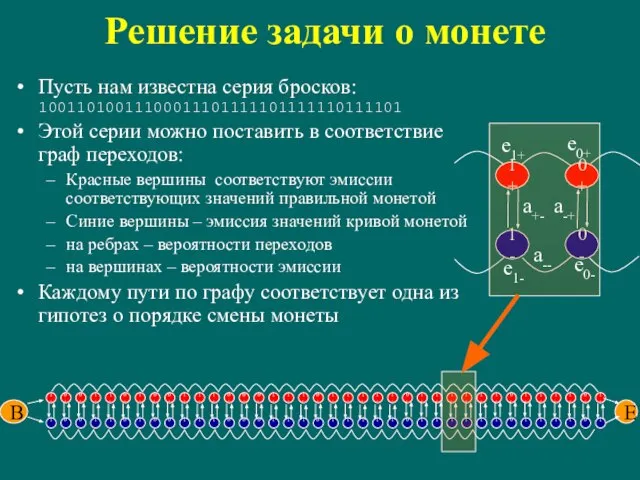
Решение задачи о монете
Пусть нам известна серия бросков:
10011010011100011101111101111110111101
Этой серии можно поставить в соответствие граф переходов:
Красные вершины соответствуют эмиссии соответствующих значений правильной монетой
Синие вершины – эмиссия значений кривой монетой
на ребрах – вероятности переходов
на вершинах – вероятности эмиссии
Каждому пути по графу соответствует одна из гипотез о порядке смены монеты
1+
0+
0+
0+
0+
1+
1+
1+
0+
1+
0+
1+
0+
1+
1+
1+
1+
1+
1+
0+
0+
0+
0+
0+
1+
1+
1+
1+
1+
1+
1+
1+
1+
1+
1+
1+
1+
1+
1-
0-
0-
0-
0-
1-
1-
1-
0-
1-
0-
1-
0-
1-
1-
1-
1-
1-
1-
0-
0-
0-
0-
0-
1-
1-
1-
1-
1-
1-
1-
1-
1-
1-
1-
1-
1-
1-
B
E
1+
0+
1-
0-
a--
e0-
a+-
a-+
e1-
e1+
e0+

Решение задачи о монете
Для любого пути можно подсчитать вероятность того, что наблюденная серия соответствует этому пути (порядку смены монет)
P = a0,1• ∏ ai,i+1• ei+1
Найдем путь, отвечающий максимуму P. log является монотонной функцией, поэтому можно прологарифмировать формулу для вероятности.
π*= argmin {– log a01 –∑π (log(ai,i+1) + log(ei+1 )}
Это задача поиска оптимального пути на графе. Решается динамическим программированием
Алгоритм динамического программирования для поиска наиболее вероятного пути называется Viterbi

Viterbi рекурсия
Обозначения
vk(i) – наилучшая вероятность пути, проходящего через позицию i в состоянии k.
πk(i) – наилучший переход из позиции i в состоянии k в предыдущую позицию (предыдущее состояние)
π*(i) – наилучшее состояние в позиции i
Инициация
vk(0) = δ(0,k); k – номер состояния
Рекурсия
vk(i) = ek(xi) maxm( vm( i-1 ) amk);
π(i,k) = argmaxm( vm( i-1 ) amk); обратный переход
Завершение
P(x,π*)= maxm( vm( L ) am0);
π*(L) = argmaxm( vm ( L ) am0);
Оптимальный путь
π*( i-1 ) = π ( i, π* ( i ) ) ;

Другая постановка задачи
Для каждого наблюденного значения определить вероятность того, что в этот момент монета была правильной.
Для этого надо просуммировать по всем путям, проходящим через точку i+ вероятности этих путей. Для решения этой задачи достаточно вспомнить динамическое программирование над полукольцом с использованием операции сложения и умножения.
Оцениваем значение
P(x, πi=k) = P(x1…xi, πi=k) •P(xi+1…xL | πi=k)/P(x);
Первый сомножитель fk(i) = P(x1…xi, πi=k) определяем просмотром вперед
Второй сомножитель bk (i+1) = P(xi+1…xL | πi=k) определяем просмотром назад

Оценка параметров HMM
Есть две постановки задачи.
Есть множество наблюдений с указанием, где происходит смена моделей (обучающая выборка, training set)
Есть множество наблюдений, но смена моделей нам не дана
В обоих случаях предполагается известными сами модели, т.е. конечные автоматы описаны, но неизвестны числа на стрелках и вероятности эмиссии.

Оценка параметров HMM при наличии обучающей выборки
Здесь используется техника оценки параметров методом наибольшего правдоподобия.
Пусть
xn – набор независимых наблюдений
θ – набор параметров, которые надо оценить
Тогда надо максимизировать θ* =argmax θ l(x1… xn | θ) = argmax θ {∑ j log P(xj | θ)}

Оценка параметров HMM при наличии обучающей выборки
Можно показать, что при большом количестве наблюдений справедливы оценки
akl = Akl / ∑l'Akl' ; ek(b) = Ek(b) / ∑b'Ek(b);
Akl – наблюденное количество переходов между моделями
Ek(b) – количество порожденных символов в соответствующих моделях
При малых размерах выборки используют технику псовдоотсчетов, добавляя к наблюденным значениям некоторое количество шума.

Если нет обучающей выборки
Итеративный алгоритм Баума-Велча.
Выберем некоторые наборы параметров HMM (обычно они генерируются случайно).
Найдем для них оптимальные пути во всех представленных примерах
По найденным оптимальным путям определим новые параметры
Перейдем к шагу 2.
Показано, что алгоритм сходится (отношение правдоподобия растет на каждой итерации)
Есть опасность нахождения локального, а не глобального экстремума.

Оценки параметров по Бауму-Велчу
Имея заданные параметры модели можно определить вероятность перехода между состояниями:
P(πi=k, πi+1=l | x,θ) = fk(i)aklei(xi+1)bl(i+1)/P(x),
где fk(i) = P(x1…xi, πi=k), bl(i+1) •P(xi+1…xL | πi+1=l) – значения, полученные при прямом и обратном проходе. Тогда для переходных и эмиссионных вероятностей получим оценки для количества переходов и порожденных символов:
Akl= ∑j1/P(xj) ∑i f jk(i)aklei(xi+1)b jl(i+1);
Ek(b) = ∑j1/P(xj) ∑i f jk(i) b jk(i) δ(x ji,b);
где x j – j-последовательность в выборке,
f jk , b jl – результаты прямого и обратного прохода по последовательности x j

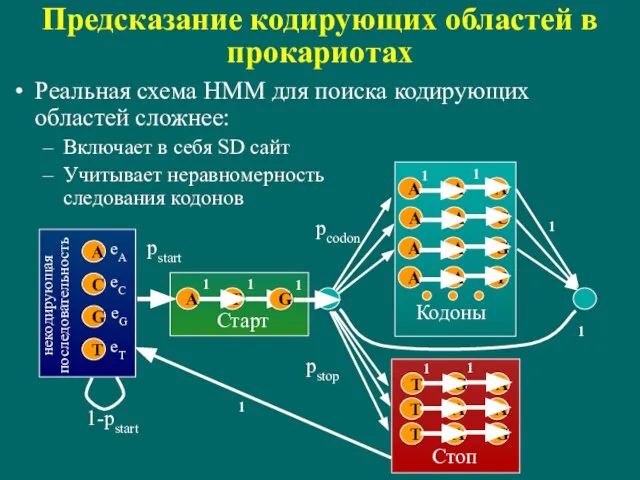
Предсказание кодирующих областей в прокариотах
Реальная схема HMM для поиска кодирующих областей сложнее:
Включает в себя SD сайт
Учитывает неравномерность
следования кодонов
A
C
G
T
eA
eC
eG
eT
A
T
1
1
A
A
C
A
A
G
A
A
T
A
A
A
1
1
Кодоны
pcodon
G
1
1
1
T
G
A
1
1
T
A
A
T
A
G
Стоп
pstart
pstop
1
1-pstart
Старт
некодирующая
последовательность

Оценка качества обучения
Выборку разбивают на два подмножества – обучающую и тестирующую
На первой выборке подбирают параметры
На второй – тестируют и определяют качество обучения:
TP – количество правильно определенных позитивных позиций (например, кодирующих)
TN – количество правильно определенных негативных позиций (например, некодирующих)
FP – количество неправильно определенных позитивных позиций (некодирующих, предсказанных как кодирующие)
FN – количество неправильно определенных негативных позиций (кодирующих некодирующих, предсказанных как некодирующие)
Специфичность:
Sp = TP / (TP + FP)
Чувствительность:
Sen =
Качество
QQ =
Коэффициент корреляции
CC =

Профили

Способы описания
множественного выравнивания
Дано: множественное выравнивание.
Задача: определить принадлежит ли некая последовательность данному семейству.
Простейший способ описания множественного выравнивания – консенсус – все просто и ясно – пишется наиболее часто встречающаяся буква
Регулярное выражение (используется в Pro-Site): L[ST]XX…
Матрица частот встречаемости аминокислот в колонке
LSPADKTNVKAAWGKV
LTPEEKSAVTALWGKV
LSEGEWQLVLHVWAKV
LSADQISTVQASFDKV
LSAAEKTKIRSAWAPV
LTESQAALVKSSWEEF
LSAAQRQVIAATWKDI
Ls......v.a.W.kv
L7...............
S.5.1............
T.2..............
P..2.............
E..213...........
A..33............
G...1............
D...11...........
Q....3...........

Энтропия колонки
Пусть колонка содержит nα букв типа α. Тогда вероятность появления такой колонки при случайных независимых последовательностях будет определяться мультиномиальным распределением:
N!
P column = ∏α pαnα ; pα – вероятность появления α
∏α nα!
Логарифм этой величины равен:
log ( P column) = log N! + ∑ α (nα log pα – log nα!)
Заменим n на N f α (f α – частота) и применим оценку для факториала n!≈ (n/e) n. Получим полную энтропию колонки
H column = log( P column) = N ∑ α f α (log pα – log f α ); доказать!
Величина
I = – ∑ α f α (log pα – log f α )
называется информационным содержанием колонки

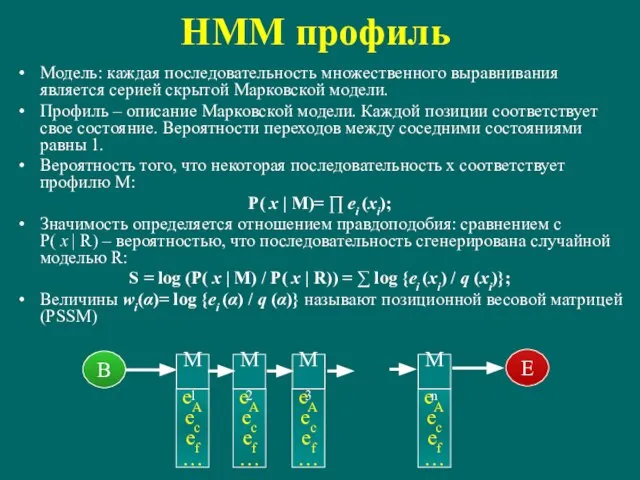
HMM профиль
Модель: каждая последовательность множественного выравнивания является серией скрытой Марковской модели.
Профиль – описание Марковской модели. Каждой позиции соответствует свое состояние. Вероятности переходов между соседними состояниями равны 1.
Вероятность того, что некоторая последовательность x соответствует профилю M:
P( x | M)= ∏ ei (xi);
Значимость определяется отношением правдоподобия: сравнением с
P( x | R) – вероятностью, что последовательность сгенерирована случайной моделью R:
S = log (P( x | M) / P( x | R)) = ∑ log {ei (xi) / q (xi)};
Величины wi(α)= log {ei (α) / q (α)} называют позиционной весовой матрицей (PSSM)
B
eA
ec
ef
…
eA
ec
ef
…
eA
ec
ef
…
eA
ec
ef
…
E
M1
M2
M3
Mn

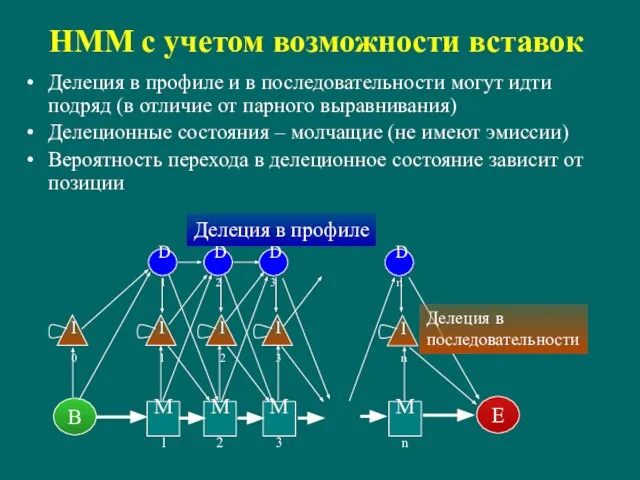
HMM с учетом возможности вставок
Делеция в профиле и в последовательности могут идти подряд (в отличие от парного выравнивания)
Делеционные состояния – молчащие (не имеют эмиссии)
Вероятность перехода в делеционное состояние зависит от позиции
B
E
M1
M2
M3
Mn
D1
D2
D3
Dn
Делеция в профиле
Делеция в
последовательности

Определение параметров модели
Для начала надо определиться с длиной модели. В случае, если обучающее множественное выравнивание не имеет вставок/делеций это тривиально. Наличие же вставок/делеций требует различать вставки и делеции. Простейшее правило если колонка содержит больше половины вставок, то она не включатся в модель, а события вставок трактуются как вставки в последовательность.
Если выравнивание толстое, то для параметров можно использовать обычные оценки:
akl = Akl / ∑l' Akl' ; ek (a) = Ek / ∑a' Ek(a');

Для тонких выравниваний
Простейшие варианты псевдоотсчетов:
Правило Лапласа: к каждому счетчику
прибавить 1:
ek (a) = (Ek(a) +1) / (∑a' Ek(a')+ Nα);
где Nα – размер алфавита (20)
Добавлять псевдоотсчеты, пропорционально фоновым частотам:
ek (a) = (Ek(a) +Aqa) / (∑a' Ek(a')+ A); A≈ Nα;
Такие псевдоотсчеты соответствуют Байесовой оценке
P(θ | D) = P(D | θ) P(θ) / P(D) ;
при априорном распределении P(θ) – распределение Дирихле с параметром αa= Aqa.

Смеси Дирихле
Представим себе, что на распределение вероятностей влияют несколько источников – частота встречаемости символа в белках вообще, частота встречаемости символа в петлях, частота встречаемости символа в трансмембранных сегментах и т.п. Каждое такое распределение дает свои псевдоотсчеты αk. Тогда для вероятности эмиссии можно написать:
ek (a) = ∑d P(d| Ek) (Ek(a) + αda) / (∑a' Ek(a')+ αda');
где P(d| Ek) – вероятность выбора распределения d при условии наблюдаемых частот:
P(d| Ek) = P(Ek | d) P(d) / ∑d' P(Ek | d') P(d') ;
Для оценки P(Ek | d) используют простую формулу:
(∑aEk(a))! Γ(∑a(Ek(a) + αda)) Γ(∑αda)
P(Ek | d)=
∏a Ek(a)! ∏a Γ(Ek(a) + αda) ∏a Γ(αda)

Использование матрицы замен
Еще один способ введения псевдоотсчетов. У нас есть матрица замен аминокислотных остатков (например, PAM120). Матрица замен моет трактоваться как то, что каждая аминокислота является немножко другой аминокислотой. Поэтому в качестве псевдоотсчетов используют величину
αja = A∑b fib P(a | b),
где fib – частота встречаемости в колонке буквы b, P(a | b) – вероятности замены буквы b на a

Использование предка
Все последовательности xk в выравнивании произошли от общего предка y.
P(yj=a | alignment)=qa∏kP(xkj|a)/∑a' qa∏kP(xkj|a)
Тогда для оценки эмиссионной вероятности
ej (a) = ∑a' Pj(a| a') P(yj=a' | alignment)
где Pj (a| a') – матрица замен. Матрица замен зависит от скорости эволюции соответствующей колонки. Для выбора матрицы можно использовать принцип максимального правдоподобия:
P(xj1, xj2,…, xjN) = ∑a' qa∏kP(xkj| a, t) → max ;
Для матрицы замен можно использовать выражение:
P(a|b, t) = exp( t P(a|b, 1) )

А чему же равно A?
Для компенсации малости выборок используют псевдоотсчеты.
Разные подходы дают разные распределения псвдоотсчетов αi, но не определяют величину коэффициента A при αi.
Часто предполагают, что псевдоотсчеты должны быть сопоставимыми с точностью определения частот Δ, которая пропорциональна Δ ≈√N, где N – количество испытаний (толщина выравнивания) поэтому полагают:
A=κ √N, κ ≈ 1 (0.5…1);

Это еще не все …
При вычислении эмиссионных вероятностей используется предположение о независимости испытаний. Однако, в выравнивании часто встречаются близкие последовательности, и это предположение неверно. Например, если мы в выравнивание добавим много копий одной из последовательностей, то эмиссионные вероятности будут в основном отражать свойства именно этой последовательности.
Пример: выравнивание содержит последовательности белка из человека, шимпанзе, гиббона, орангутанга, мыши, рыбы, мухи, комара, червяка. Очевидно, что последовательности приматов перепредставлены. Кроме того, последовательности двукрылых также перепредставлены.
Поэтому при подсчете вероятностей необходимо каждую последовательность учитывать с весом, отражающем ее уникальность в данной выборке.

Взвешивание последовательностей
Способ учета неравномерной представленности последовательностей в выборке называется взвешиванием последовательностей.
Каждой последовательности в выравнивании присваивается свой вес βk. Тогда частота каждого символа a в колонке k подсчитывается по формуле:
Eak = ∑i βi δ(S ik , a) / ∑ βi
где S ik – буква в последовательности i в колонке k, βi – вес последовательности i.

Взвешивание последовательностей Метод Герштейна-Сонхаммера-Чотьи
Пусть нам известно филогенетическое дерево с расстояниями на ветвях. На листьях – последовательности.
В начале все веса последовательностей приравниваются длинам веток
Далее веса определяем итеративно, внося поправки в веса по ходу движения вверх по дереву:
Δwi=tn wi/ ∑k-листья ниже узла n wi
Смысл заключается в том, что длиня ветки распределяется по дочерним узлам

Взвешивание последовательностей Многогранники Воронова
Поместим объекты в некоторое метрическое пространство. Каждый объект хочет иметь "поместье" – некоторую область пространства. Проведем границы между поместьями посередине между объектами. В результате все "поместья" будут иметь форму многогранника. Эта конструкция называется многогранниками Воронова.
Можно определить вес последовательности как объем поместья. Вопрос только в том как и в какое метрическое пространство помещать последовательности.

Вероятность модели при условии, что последовательность x принадлежит модели M:
P( x | M) P(M)
P(M | x) =
P( x | M)P(M) + P( x | R)(1-P(M)
Вероятность модели при условии нескольких последовательностей (дискриминатор):
D=∏k P( M | xk)
Веса последовательностей подбираем так, чтобы максимизировать D.
Но: чтобы вычислить D нам необходимы параметры модели, которые зависят от того, как мы взвешивали последовательности. Применяют итеративную процедуру.
Взвешивание последовательностей Максимально дискриминирующие веса

Взвешивание последовательностей Максимизация энтропии
Пусть k(i,a) – количество остатков типа a в колонке i, mi – количество типов остатков в колонке i. Выберем вес для последовательности k равным
wk(i)=1/(mi k(i,a)).
Такой вес обеспечивает наиболее равномерное распределение частот остатков в колонке. Чтобы задать вес для последовательности в целом, просуммируем соответствующие веса:
wk = ∑i wk(i) = ∑i 1/(mi k(i,a)).

Обобщенный подход:
∑i Hi(w) → max, ∑kwk=1;
где Hi(w) = ∑a pia log pia;
pia – вероятности встречаемости аминокислоты a в колонке i, подсчитанные с учетом весов последовательностей:
pia= ∑k wk δ ( xki, a);
Задача максимизации приводит к системе уравнений:
∑kwk=1;
∑i ∂ Hi(w)/ ∂wk – λ = 0;
Здесь неизвестные wk и неопределенный множитель Лагранжа λ
Взвешивание последовательностей Максимизация энтропии

Множественное выравнивание

Множественное выравнивание
Способ написать несколько последовательностей друг под другом (может быть с пропусками) так, чтобы в одной колонке стояли гомологичные позиции.
"Золотой стандарт" – совмещенные пространственные структуры гомологичных белков. Соответствующие позиции в разных последовательностях отвечают гомологичным позициям
Задача. Найти способ (алгоритм и параметры), выравнивающий последовательности "золотого стандарта" правильно. Есть надежда, что в случаях, когда пространственные структуры неизвестны, этот алгоритм правильно выровняет последовательности.

Оценка качества множественного выравнивания
Энтропийная оценка
Обычно считают, что колонки в выравнивании независимы. Поэтому качество выравнивания можно оценить как сумму качеств колонок:
S = G + ∑columns S(mk)
G – веса делеций, S(mk) – вес колонки
Пусть сia – количество появлений аминокислоты a в колонке i. Вероятность колонки можно описать как
P(mi) = ∏apiacia
Вероятность выравнивания = ∏iP(mi); В качестве веса можно использовать логарифм вероятности:
S = ∑columns S(mk);
S(mk) = – ∑acialog pia = H(mi)
H(mi) – энтропия колонки; для вероятностей остатков принимают:
pia = c~ia / ∑a' c~ia'
где c~ia – количество остатков в колонке с поправкой на псевдоотсчеты

Оценка качества множественного выравнивания
Сумма пар
Другой традиционный способ оценки – сумма весов матрицы соответствия аминокислотных остатков SP:
S(mi) = ∑k
Способ не совсем правильный. Более правильная оценка для трех последовательностей S(mi) = log (pabc / qaqbqc), а не log (pab/qaqb) + log (pbc/qbqc) + log (pac/qaqc); (вспомним определение матрицы замен)

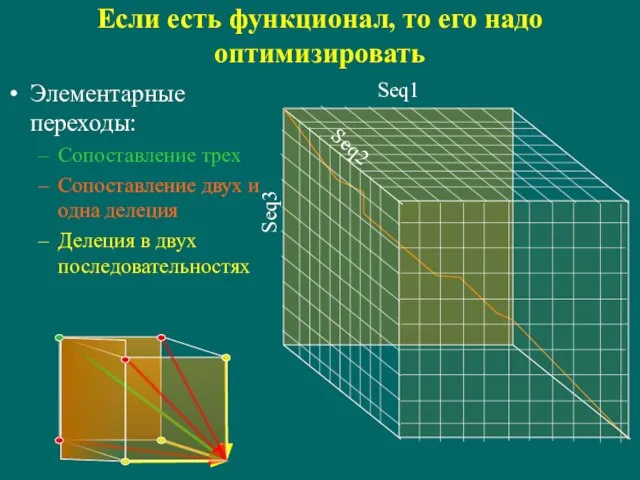
Если есть функционал, то его надо оптимизировать
Элементарные переходы:
Сопоставление трех
Сопоставление двух и одна делеция
Делеция в двух последовательностях
Seq1
Seq2
Seq3

Динамическое программирование для множественного выравнивания
Количество вершин равно ∏посл. Li = O(LN)
Количество ребер из каждой вершины = 2N-1 (почему ?)
Количество операций равно
T = O(LN)
Надо запоминать обратные переходы в LN вершинах.
Если количество последовательностей > 4, то задача практически не разрешима.

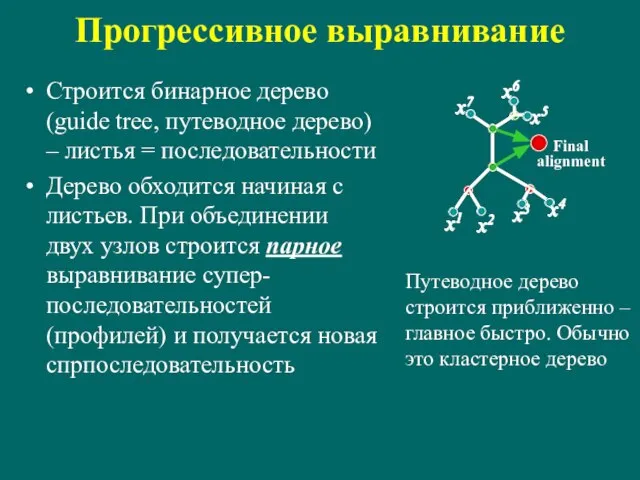
Прогрессивное выравнивание
Строится бинарное дерево (guide tree, путеводное дерево) – листья = последовательности
Дерево обходится начиная с листьев. При объединении двух узлов строится парное выравнивание супер-последовательностей (профилей) и получается новая спрпоследовательность
Путеводное дерево строится приближенно – главное быстро. Обычно это кластерное дерево

Выравнивание профилей
Выравнивание одной стопки последовательности относительно другой – обычное динамическое программирование.
Оптимизируется сумма парных весов:
∑i S(mi) → max
S(mi) = ∑k< l≤N s(xki, xli)
Если мы выравниваем две стопки – 0 < i ≤ n и n < i ≤ N, то сумму разбиваем на три части:
S(mi) = ∑k< l≤n s(xki, xli) + ∑n< k< l≤N s(xki, xli) +
∑k≤n, n< l≤N s(xki, xli)
Две первые суммы являются внутренним делом стопок, последняя сумма отвечает за сравнение стопок (профилей)
При сравнении используем расширенную матрицу сходства, добавив в нее сравнение делционного символа '-' :
s(-,-)=0, s( a ,-) = -d ;
При множественном выравнивании обычно используют линейные штрафы за делеции

ClustalW
Строится матрица расстояний с использованием попарных выравниваний
Строится NJ дерево (метод ближайшего соседа)
Строится прогрессивное выравнивание
Используются дополнительные эвристики:
Взвешивание последовательностей (с учетом только топологии дерева)
На разных уровнях дерева используются разные матрицы сходства
Используется контекстно-зависимые штрафы за открытие делеции
Если при построении выравнивания появляются очень низкие веса, то дерево корректируется

Улучшение выравнивания
Недостаток прогрессивных методов: если для некоторой группы последовательностей выравнивание построено, то оно уже не перестраивается.
Алгоритм итеративного улучшения
Вынимаем из выравнивания одну последовательность
По оставшимся последовательностям строим профиль
Выравниваем вынутую последовательность с профилем
Переходим к этапу 1.

Множественное выравнивание с помощью HMM
Каждому множественное выравнивание соответствует скрытая Марковская модель.
Можно применить алгоритм максимизации ожидания Баума-Велча:
Порождаем случайные параметры HMM.
Выравниваем все последовательности с этой моделью
Переоцениваем параметры.
Проблема: легко попасть в локальный максимум
Обход проблемы: время от времени параметры HMM возмущаются.
Другой вариант – использование искусственного отжига.
Достоинство подхода: одновременно анализируются все последовательности. Нет проблемы необратимости, характерной для прогрессивного выравнивания.

Блочное выравнивание

Поиск сигналов

Постановка задачи
Дано несколько (например,20) последовательностей. Длина каждой последовательности - 200
В каждой последовательности найти короткий (длиной 20) фрагмент (сайт), такой, что все сайты между собой похожи.
Например, даны регуляторные области совместно регулируемых генов. Найти сайты связывания белков-регуляторов.

Графвая постановка задачи.
Дан многодольный граф:
Каждой доле соответствует последовательность
Вершины – сайты
Ребра проводятся между всеми сайтами, или если эти сайты между собой похожи.
На каждой клике графа определено число. Например, информационное содержание безделеционного множественного выравнивания сайтов
Найти клику наибольшего веса
attcgctgac
catcgctaac
ctttgcaatg

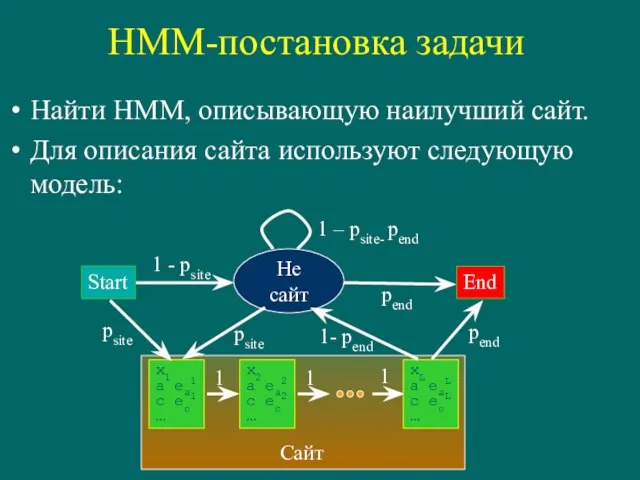
HMM-постановка задачи
Найти HMM, описывающую наилучший сайт.
Для описания сайта используют следующую модель:
Start
Не сайт
x1
a ea1
c ec1
…
x2
a ea2
c ec2
…
xL
a eaL
c ecL
…
End
Сайт
1
1
1
1- pend
1 – psite- pend
1 - psite
psite
pend
psite
pend

Алгоритм максимизации ожидания
Допустим нам приблизительно известна структура сайта.
Применяем алгоритм Баума-Велча.
Получаем структуру сайта.
Алгоритм MEME:
В качестве исходной модели выбираем модель, индуцированную первым словом в первой последовательности (с учетом псевдоотсетов).
Находим HMM
Берем в качестве исходной следующее слово из первой последовательности.
Так перебираем все слова во всех последовательностях
Отбираем наилучшие HMM

Гиббс сэмплер
Задача: найти набор позиций сайтов в последовательностях
Инициация: В качестве решения выбираем произвольный набор позиций.
Итерации:
Удаляем из выборки одну последовательность.
По позициям, определенным для остальных последовательностей строим профиль (HMM).
Для каждой позиции в удаленной последовательности рассчитываем вероятность того, что сайт находится там.
Разыгрываем позицию сайта в удаленной последовательности в соответствии с рассчитанными вероятностями.
Повторяем процедуру много раз для всех последовательностей

Вероятности для Гиббс сэмплера
Вероятности для Гиббс сэмплера

Комбинаторные методы

RNA

Вторичная структура РНК
Вторичной структурой называется совокупность спаренных оснований
Биологическая роль вторичной структуры:
Структурная РНК –
рибосомная,
тРНК
Регуляция –
Рибопереключатели
аттенюация
микроРНК
Рибозимы
Стабильность РНК

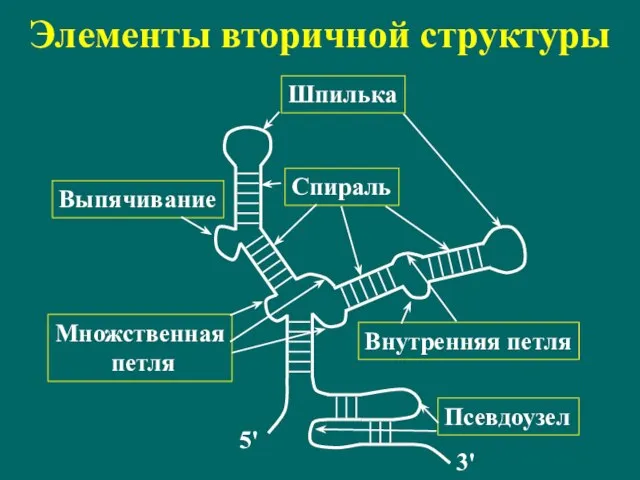
Элементы вторичной структуры
Шпилька
Спираль
Внутренняя петля
Множственная
петля
Выпячивание
Псевдоузел
5'
3'

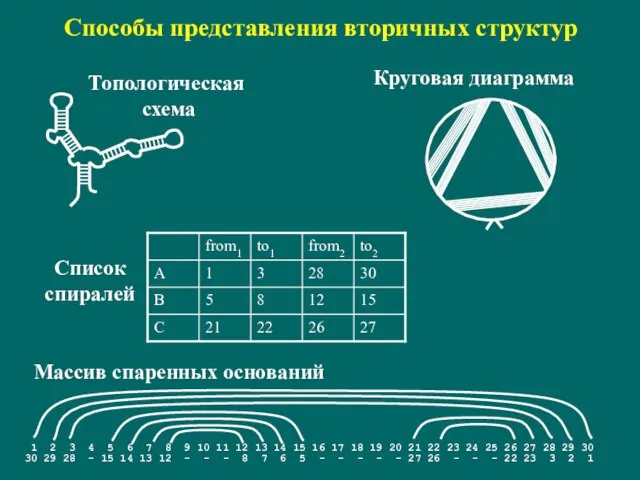
Способы представления вторичных структур
Топологическая
схема
Круговая диаграмма
Массив спаренных оснований
Список
спиралей

Задача
Дана последовательность.
Найти правильную вторичную структуру.
Золотой стандарт: тРНК, рРНК.
Количество возможных вторичных структур очень велико.
Дополнительные ограничения:
Нет псевдоузлов. (На самом деле они очень редки и энергетически невыгодны)
Количество возможных структур все равно очень велико
Надо найти оптимальную структуру. А что оптимизировать? Как оптимизировать?

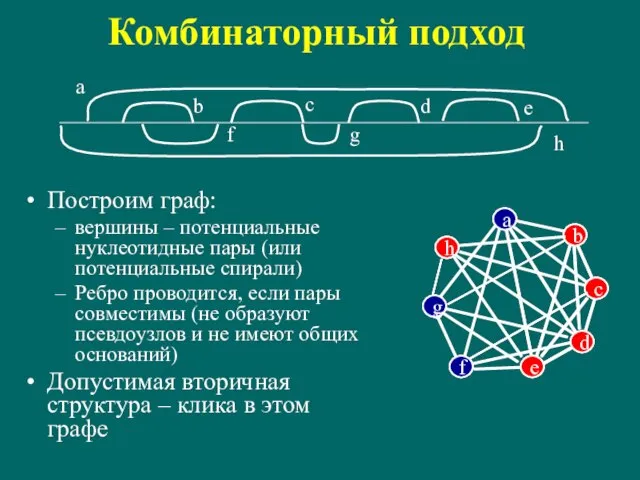
Комбинаторный подход
Построим граф:
вершины – потенциальные нуклеотидные пары (или потенциальные спирали)
Ребро проводится, если пары совместимы (не образуют псевдоузлов и не имеют общих оснований)
Допустимая вторичная структура – клика в этом графе
a
b
c
d
e
f
g
h

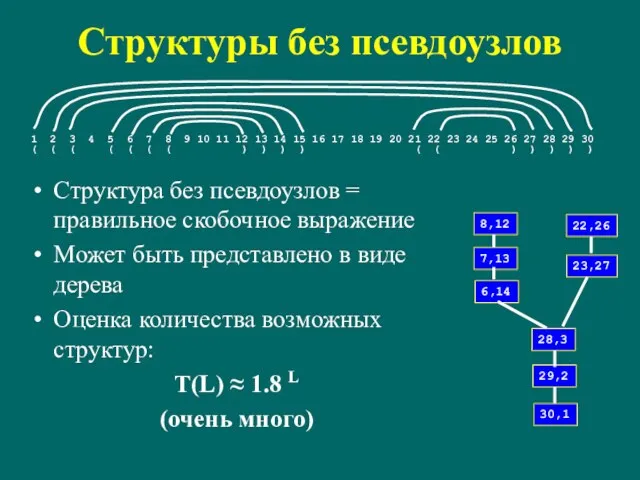
Структуры без псевдоузлов
Структура без псевдоузлов = правильное скобочное выражение
Может быть представлено в виде дерева
Оценка количества возможных структур:
T(L) ≈ 1.8 L
(очень много)
28,3
22,26
8,12
23,27
6,14
7,13
29,2
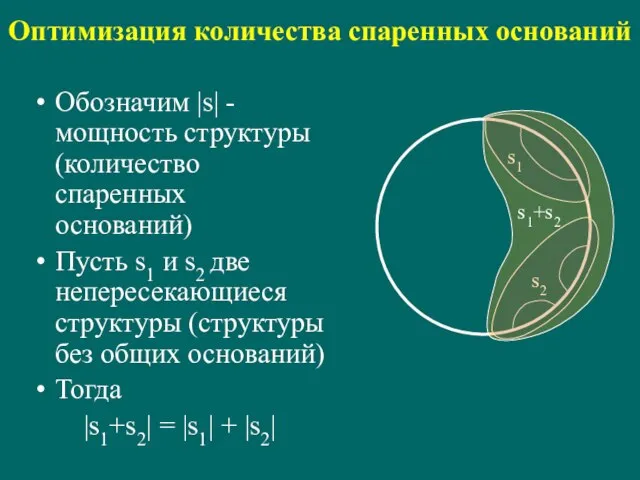
30,1

Оптимизация количества спаренных оснований
Обозначим |s| - мощность структуры (количество спаренных оснований)
Пусть s1 и s2 две непересекающиеся структуры (структуры без общих оснований)
Тогда
|s1+s2| = |s1| + |s2|
s2
s1
s1+s2

Оптимизация количества спаренных оснований
Пусть нам известны оптимальные структуры Srt для всех фрагментов
i≤ r ≤ t ≤ j
Тогда можно найти оптимальную структуру для сегмента [i, j+1]
Для этого нам надо понять, спаривать ли основание j+1, и, если спаривать, то с кем
i+1
k
Sk+1,i
S1,k-1

Динамическое программирование для количества спаренных оснований (Нуссинофф)
Количество спаренных оснований в оптимальной структуре S*i,j+1 определяется как максимум:
S*i,j+1 = max {
S*i,j; (нет спаривания)
maxk (S*i,k-1 + S*k, j )+1;
(k спаривается с j+1)
};
Время работы алгоритма:
T≈O(L3)

Динамическое программирование для количества спаренных оснований
При поиске оптимального количества спаренных оснований заполняется треугольная матрица весов Si,j, i < j.
Обозначим πij – номер основания, с которым надо спарить основание j при анализе сегмента [i, j], или 0, если не надо спаривать. При оптимизации запоминаем треугольную матрицу спаривания (аналог матрицы обратных переходов)

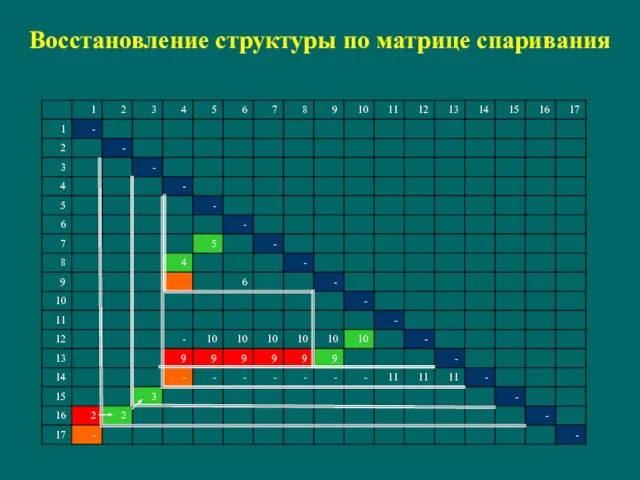
Восстановление структуры по матрице спаривания
-
-
17
-
2
2
16
-
3
15
-
11
11
11
-
-
-
-
-
-
-
14
-
9
9
9
9
9
9
13
-
10
10
10
10
10
10
-
12
-
11
-
10
-
6
9
-
4
8
-
5
7
-
6
-
5
-
4
-
3
-
2
-
1
17
16
15
14
13
12
11
10
9
8
7
6
5
4
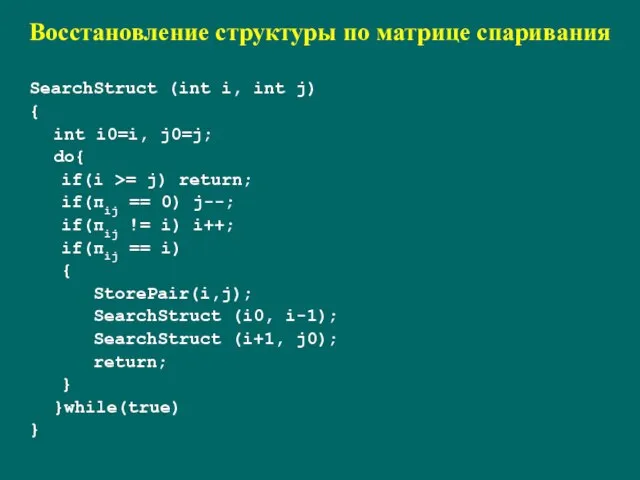
3
2
1

Восстановление структуры по матрице спаривания
SearchStruct (int i, int j)
{
int i0=i, j0=j;
do{
if(i >= j) return;
if(πij == 0) j--;
if(πij != i) i++;
if(πij == i)
{
StorePair(i,j);
SearchStruct (i0, i-1);
SearchStruct (i+1, j0);
return;
}
}while(true)
}

Энергия вторичной структуры
Энергия спиралей
Энергия петель (энтропия)
A – U
C – G
A – U
G – C
C – G
ΔG =
-3.2
-3.2
-3.7
-4.5
Энергия спирали рассчитывается как сумма энергий стэкингов
= - 14.6

Энергия петель
Энергия свободной цепи
ΔG = B + 3/2 kT ln L
Для шпилек при L=3..5 кроме энтропии есть некоторое напряжение структуры.
Для внутренних петель и для мультипетель L – суммарная длина петель + количество ветвей.
Параметр B зависит от типа петли
Для выпячивания сохраняется стэкинг.
Обычно используют не формулу, а таблицы.

Минимизация энергии
Обычное динамическое программирование не проходит – нет аддитивности.
Определения
нуклеотид h называется доступным для пары i•j , если НЕ существует спаривания k•l, такого, что
i < k < h < l < j
Множество доступных нуклеотидов для пары i•j называется петлей L ij , а пара i•j называется замыкающей парой. Частный случай петли – стэкинг.
Энергия структуры рассчитывается как сумма энергий петель (в том числе и стекингов):
ΔG = ∑ e(Lij)

Алгоритм Зукера
Введем две переменные:
W(i,j) – минимальная энергия для структуры на фрагменте последовательности [i, j];
V(i,j) – минимальная энергия для структуры на фрагменте последовательности [i, j] при условии, что i и j спарены;
Рекурсия:
V(i,j) = mini≤i1
W(i,j)=min{ W(i+1,j), i не спарено
W(i,j-1), j не спарено
V(i,j), i и j спарены
mini
i j спарены с кем-то.

Алгоритм Зукера
Рекурсия для W требует времени
T≈O(L3)
Рекурсия для V требует гораздо большего времени
T≈O(2L)
Причина – мультипетли. Можно:
Ограничить размер или индекс мультипетель
Применить упрощенную формулу для их энергии
Просматривать мультипетли только если i+1, j-1 не спарены.
Применить приближенную эвристику

Проблемы минимизации энергии
Только около 80% тРНК сворачиваются в правильную структуру
Энергетические параметры определены не очень точно. Более того, в клетке бывают разные условия, и, соответственно, реализуются разные параметры.
Находится единственная структура с минимальной энергией, в то время как обычно существует несколько структур с энергией, близкой к оптимальной.

Решение проблем
Искать субоптимальные структуры
Искать эволюционно консервативные структуры.
структуры тРНК и рРНК определены именно так

Поиск субоптимальных структур и структурных элементов
Статистическая сумма
Z = ∑ exp(-ΔGi /kT)
Если мы просуммируем по всем структурам, содержащим данную пару, то мы можем оценить ее значимость (чем Z больше, тем более значимым является спаривание)
Для подсчета Z можно использовать тот же алгоритм динамического программирования, заменив min на суммирование, а сложение на умножение.
Больцмановская вероятность того, что нуклеотиды i,j спарены равна:
P(i,j) = exp(-ΔGij /kT) /Zij ;
Разыгравыем пары оснований в соответствии с этой вероятностью и восстанавливаем соответствующие субоптимальные вторичные структуры.

Консенсусные вторичные структуры РНК

Основные задачи
Построение консенсуса
Дано: набор последовательностей для которых известно, что они имеют общую вторичную структуру (например, тРНК или регуляторный элемент)
Описать общую структуру
Поиск консенсуса
Дано: описание консенсуса.
Найти в данной последовательности (например, в геноме) все случаи встречи консенсуса

Метод ковариаций
Пусть дано множественное выравнивание последовательностей
Взаимная информация двух колонок:
I(A,B) = ∑ αβ fAB(αβ) log2{fAB(αβ) / (fB(β))}
fAB(αβ) – частоты одновременной встречи буквы α в колонке A и буквы β в колонке B.
fA(α) – частота встречаемости буквы α в колонке A.
fB(β) – частота встречаемости буквы β в колонке B.
Пары колонок с высоким значением взаимной информации с большой степенью вероятности образуют комплементарную пару (если высоки совместные частоты для пар букв AT, CG)
Для восстановления вторичной структуры можно использовать алгоритм Нуссинофф, приписывая в качестве весов пар значение взаимной информации.

Грамматики
Определения
Терминальным символом называется символ, который может получаться в строке (обозначается малыми буквами)
Нетерминальный символ – символ для обозначения промежуточной подстроки
Грамматика – набор правил генерации слов
Пример:
W2 → aW1 , W1 → bW2 , W1 → ε ;
Порождает слова вида "ababababab"

Стохастические контекстно-свободные грамматики
Контекстно-свободные грамматики имеют правила вида
W → β
β – терминальные и/или нетерминальные исключая нулевую строку
Правила преобразования могут быть снабжены вероятностями
Обобщает скрытые Марковские модели. Позволяет описывать вторичные структуры РНК.
Пример. Грамматика
S → aW1t | cW1g | gW1c | tW1a;
W1 → aW2t | cW2g | gW2c | tW2a;
W2 → aW3t | cW3g | gW3c | tW3a;
W3 → gaaa | gcaa
Порождает шпильки с длиной спирали 3 и с последовательностью в петле gaaa или gcaa

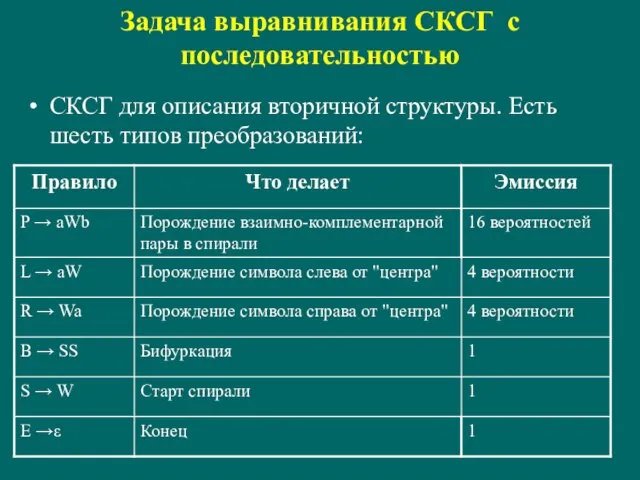
Задача выравнивания СКСГ с последовательностью
СКСГ для описания вторичной структуры. Есть шесть типов преобразований:

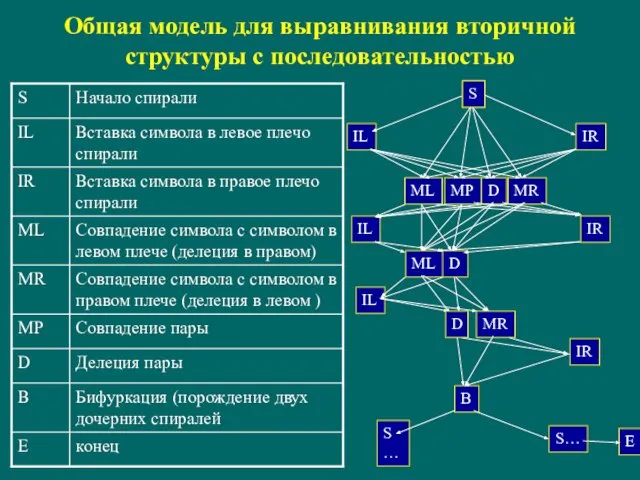
Общая модель для выравнивания вторичной структуры с последовательностью

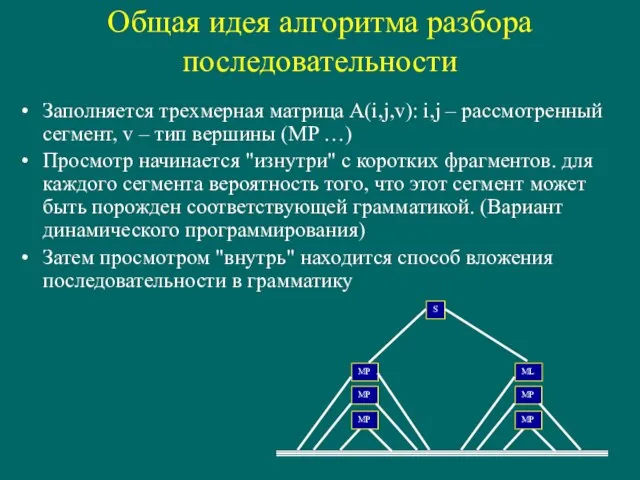
Общая идея алгоритма разбора последовательности
Заполняется трехмерная матрица A(i,j,v): i,j – рассмотренный сегмент, v – тип вершины (MP …)
Просмотр начинается "изнутри" с коротких фрагментов. для каждого сегмента вероятность того, что этот сегмент может быть порожден соответствующей грамматикой. (Вариант динамического программирования)
Затем просмотром "внутрь" находится способ вложения последовательности в грамматику
MP
MP
ML
MP
MP
MP
S

Поиск генов