Содержание
- 2. Топологическая сортировка
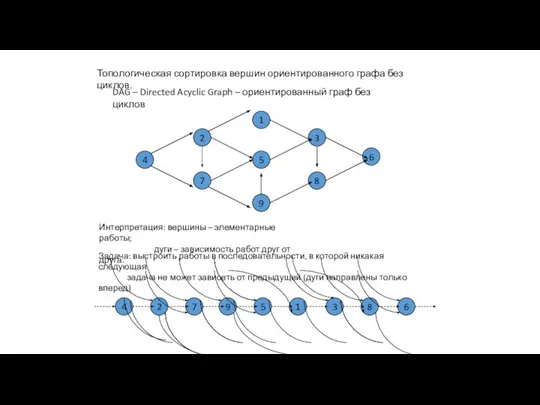
- 3. Топологическая сортировка вершин ориентированного графа без циклов. DAG – Directed Acyclic Graph – ориентированный граф без
- 4. Топологическая сортировка вершин ориентированного графа без циклов. 1 5 9 2 7 3 8 4 6
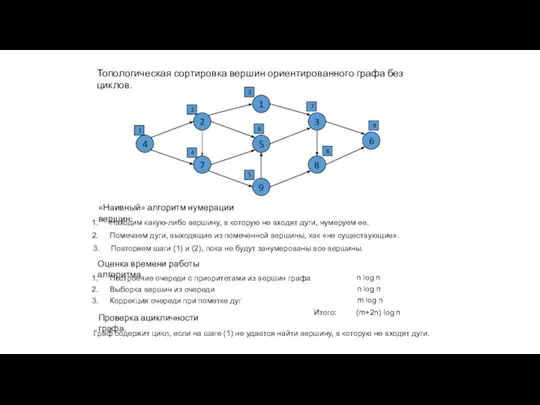
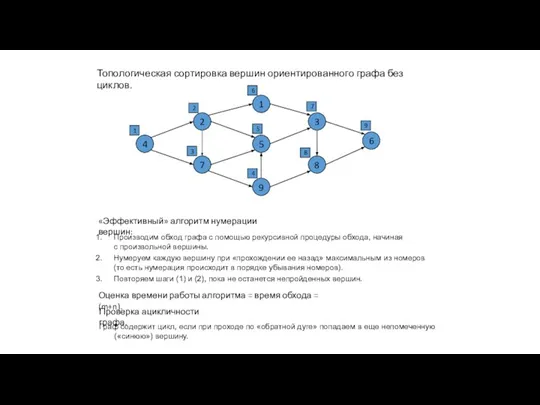
- 5. Топологическая сортировка вершин ориентированного графа без циклов. 1 5 9 2 7 3 8 4 6
- 6. Алгоритм Флойда - Уоршелла
- 7. Алгоритм Флойда - Уоршелла Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом В отличии от
- 8. Обозначения Перенумеруем вершины графа целыми числами от 1 до N. Обозначим через di,jm длину кратчайшего пути
- 9. Обозначения Обозначим через Dm матрицу размера NxN, элемент (i,j) которой совпадает с di,jm. Если в исходном
- 10. Суть алгоритма Флойда заключается в проверке того, не окажется ли путь из вершины i в вершину
- 11. Этап 1. Перенумеровать вершины графа от 1 до N, определить матрицу D0, каждый элемент di,j0 которой
- 12. Матрицу S0, в которой будем запоминать последовательность вершин в кратчайшем пути, заполним так: sij = j
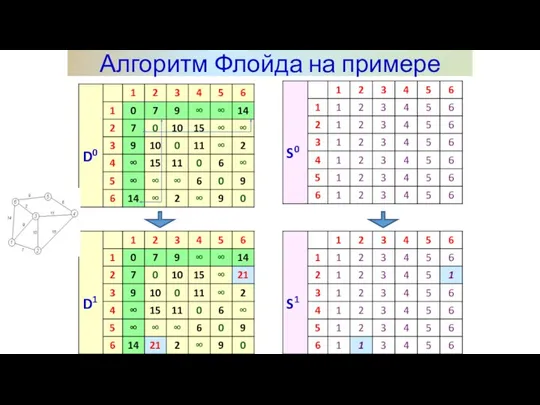
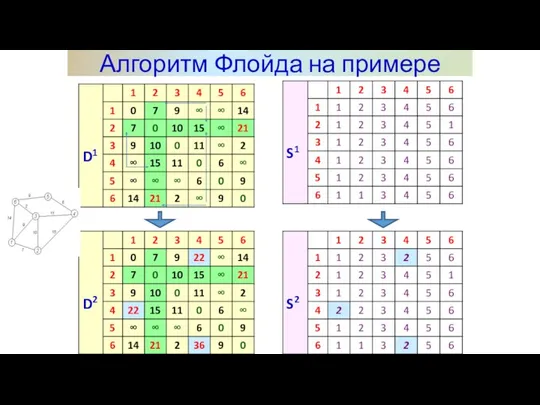
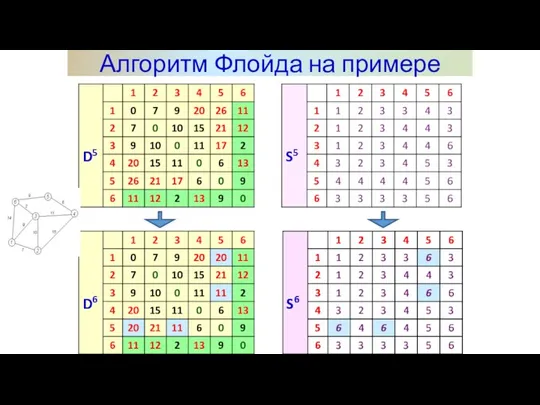
- 13. Алгоритм Флойда на примере Задаём строку m и столбец m как ведущую строку и ведущий столбец.
- 14. Алгоритм Флойда на примере
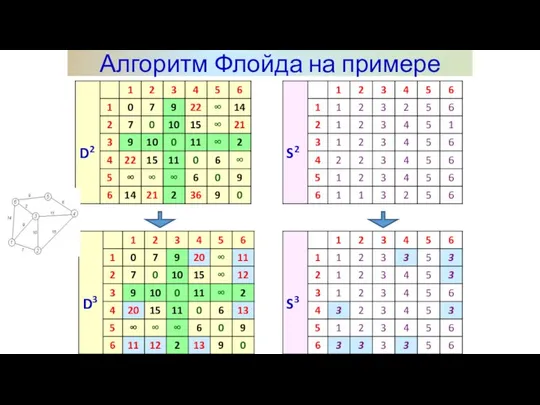
- 15. Алгоритм Флойда на примере
- 16. Алгоритм Флойда на примере
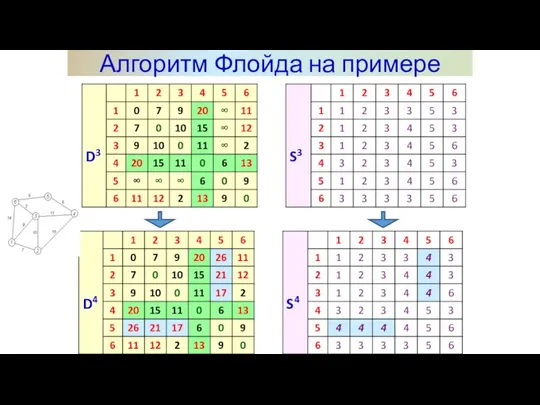
- 17. Алгоритм Флойда на примере
- 18. Алгоритм Флойда на примере
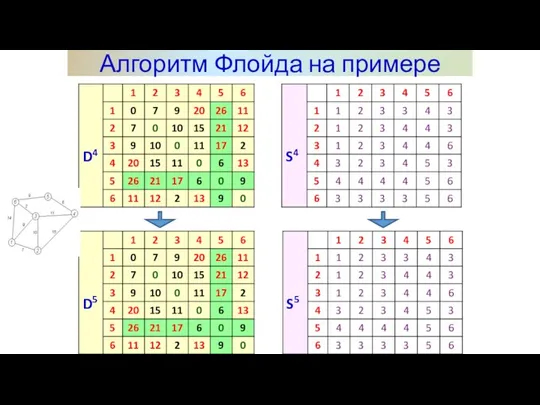
- 19. Алгоритм Флойда на примере
- 20. Алгоритм Флойда на примере Последний этап. После реализации N этапов алгоритма определение по матрицам Dn и
- 21. d25 = 21 Путь: 2->4 ->5 d51 = 20 Путь: 5->6 ->3 -> 1 Алгоритм Флойда
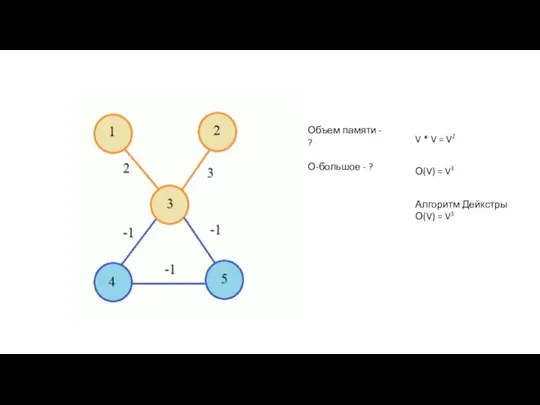
- 22. Объем памяти - ? О-большое - ? V * V = V2 О(V) = V3 Алгоритм
- 24. Волновой алгоритм (Алгоритм Ли)
- 25. Рассматривается алгоритм построения ортогонального пути. Алгоритм состоит из двух частей. В первой от источника к приемнику
- 27. Инициализация Пометить стартовую ячейку d := 0 Распространение волны ЦИКЛ ДЛЯ каждой ячейки X, помеченной числом
- 32. При обратном ходе в путь включается по одной ячейке каждого шага распространения волны. При выборе из
- 33. Алгоритм Форда – Фалкерсона
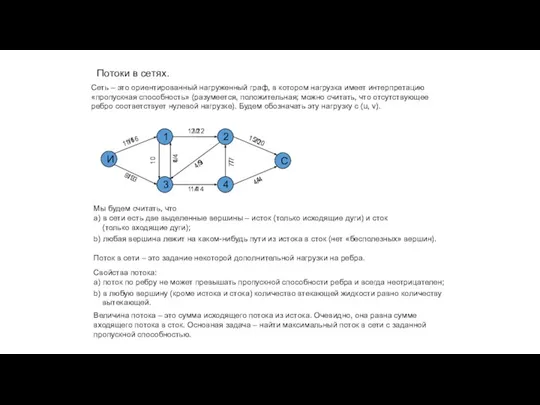
- 34. Потоки в сетях. И 1 2 3 С 4 Сеть – это ориентированный нагруженный граф, в
- 35. Потоки в сетях. И 1 2 3 С 4 Пусть задана сеть и поток в ней.
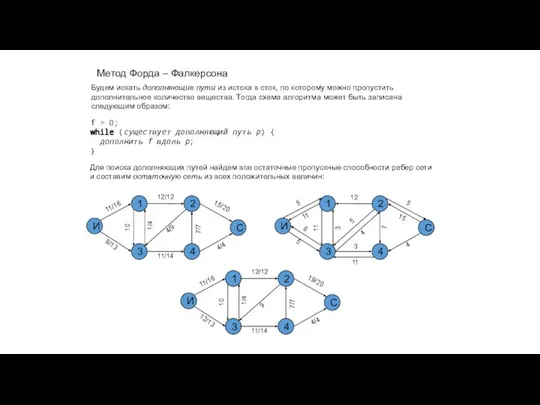
- 36. Метод Форда – Фалкерсона И 1 2 3 С 4 Будем искать дополняющие пути из истока
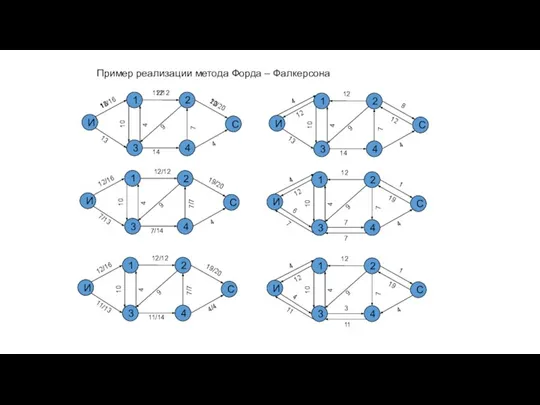
- 37. Пример реализации метода Форда – Фалкерсона И 1 2 3 С 4 10 16 12 4
- 39. Скачать презентацию























 Водорастворимые витамины
Водорастворимые витамины Занятия Мои друзья. Мое увлечение
Занятия Мои друзья. Мое увлечение Сладкие шляпки
Сладкие шляпки Открытый и закрытый слоги Eve Ken
Открытый и закрытый слоги Eve Ken ГЕОМЕТРИЯ
ГЕОМЕТРИЯ Обзор системы и процесса усыновления
Обзор системы и процесса усыновления Презентация на тему Литр (1 класс)
Презентация на тему Литр (1 класс) Презентация на тему Токсикомания
Презентация на тему Токсикомания JUVENILE justice
JUVENILE justice Что мы знаем о птицах
Что мы знаем о птицах Источники права периода централизации государства
Источники права периода централизации государства Презентация по теме: Химические реакции
Презентация по теме: Химические реакции Внутренняя модель данных
Внутренняя модель данных Местечко Ажерово и его обитатели
Местечко Ажерово и его обитатели Управление инвестиционно-строительным проектом в области складской логистики
Управление инвестиционно-строительным проектом в области складской логистики Бордюры
Бордюры Легко ли быть режиссером?
Легко ли быть режиссером? Менеджмент в ресторанном бизнесе
Менеджмент в ресторанном бизнесе Правоотношения
Правоотношения БЭСТ-5. АПТЕКАТо, что доктор прописал!
БЭСТ-5. АПТЕКАТо, что доктор прописал! Разработка и написание проекта
Разработка и написание проекта С днём рождения друг
С днём рождения друг Презентация на тему Линзы Оптика 8 класс
Презентация на тему Линзы Оптика 8 класс  ФГОС НОО (Выполнила Кибиткина С.В., учитель СОШ № 2 г. Ершова
ФГОС НОО (Выполнила Кибиткина С.В., учитель СОШ № 2 г. Ершова Духовно-нравственное становление личности
Духовно-нравственное становление личности Презентация на тему Кто что ест
Презентация на тему Кто что ест Организация и управление закупочной деятельностью
Организация и управление закупочной деятельностью Простые механизмы. Применение в быту, технике и живой природе
Простые механизмы. Применение в быту, технике и живой природе