Аналитическая геометрия

Аналитическая геометрия

Алгебраические поверхности и линии на плоскости первого порядка
Опр. Геометрическое место точек
в пространстве (на плоскости) определяет плоскость (прямую на плоскости)
тогда и только тогда, когда декартовы координаты x, y, z текущей точки М удовлетворяют алгебраическому уравнению первого порядка

Геометрический смысл нормального вектора
Задача 1. На плоскости дана точка и вектор . Составить уравнение прямой на плоскости, проходящей через точку перпендикулярно вектору.
Рассмотрим текущую точку прямой
тогда вектор
лежит на данной прямой.
С
Вектор

Нормальный вектор – вектор, перпендикулярный прямой.

Задача 2.
В пространстве дана точка и вектор . Составить уравнение плоскости, проходящей через точку перпендикулярно вектору.
Рассмотрим текущую точку прямой
вектор
лежит на плоскости.
D
Вектор

Нормальный вектор – вектор, перпендикулярный плоскости.

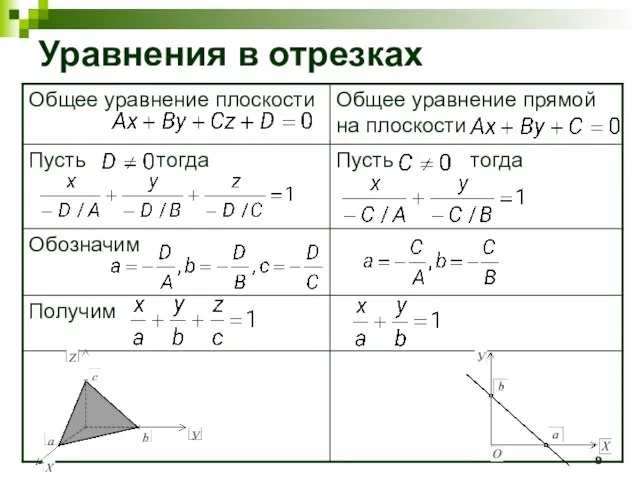
Уравнения в отрезках

Исследование уравнения прямой

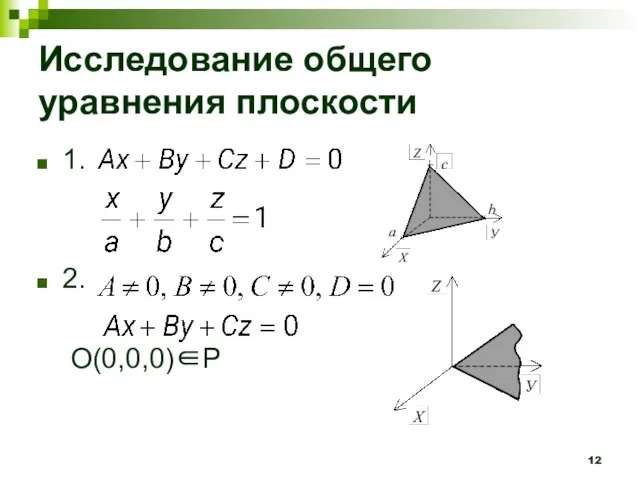
Исследование общего уравнения плоскости
1.
2.
O(0,0,0)∈P

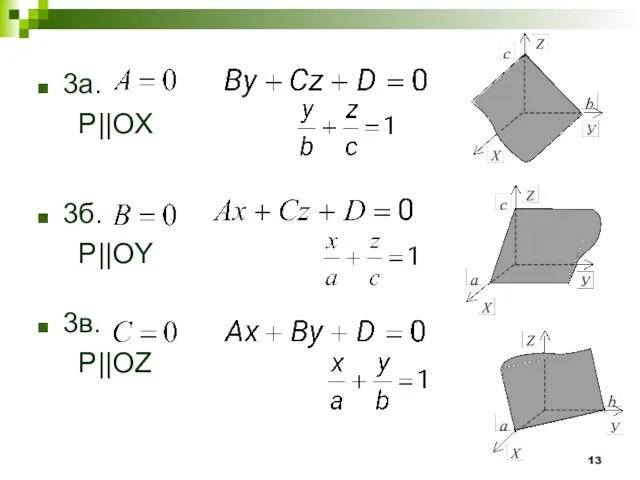
3а.
P||OX
3б.
P||OY
3в.
P||OZ

4а.
P||XOY
4б.
P||XOZ
4в.
P||YOZ

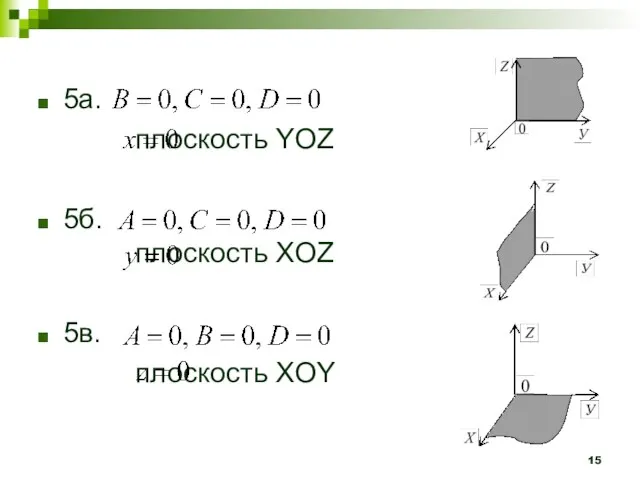
5а.
плоскость YOZ
5б.
плоскость XOZ
5в.
плоскость XOY

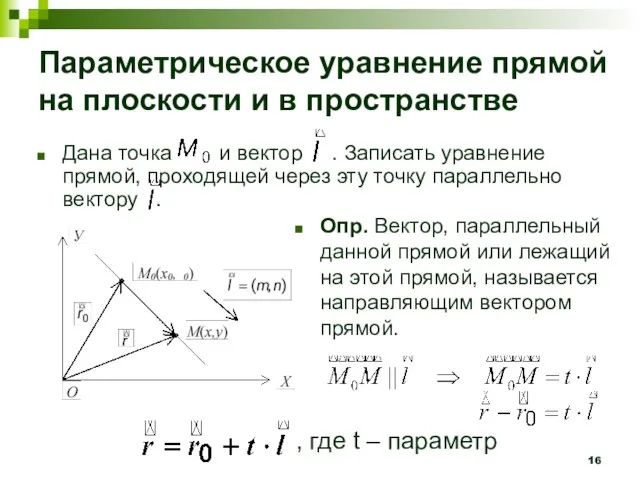
Параметрическое уравнение прямой на плоскости и в пространстве
Дана точка и вектор . Записать уравнение прямой, проходящей через эту точку параллельно вектору .
Опр. Вектор, параллельный данной прямой или лежащий на этой прямой, называется направляющим вектором прямой.
, где t – параметр

Каноническое уравнение прямой на плоскости и в пространстве
Если исключить параметр t из параметрического уравнения, то получим каноническое уравнение прямой.

Уравнение прямой проходящей через две точки М1 и М2

Параметрическое уравнение плоскости
Дана точка и два неколлинеарных вектора Составить уравнение плоскости, проходящей через точку параллельно векторам .
Векторы компланарны, ⇒ линейно зависимы ⇒ один из них является линейной комбинацией остальных, т.е.
p, q – параметры
или

Уравнение плоскости, проходящей через точку параллельно двум векторам
Т.к. векторы компланарны, то