Содержание
- 2. Литература А.Б.Сергиенко. Цифровая обработка сигналов. – СПб.: Питер, 2003 г. Лайонс Р. Цифровая обработка сигналов. пер.
- 3. Темы Спектральный анализ БПФ Гребенка фильтров Непараметрические методы оценивания СПМ Полифазное БПФ Другие методы Формирование цифровых
- 4. Методы цифрового спектрального анализа Основные приложения: радиолокация, радионавигация, радиоастрономия; гидроакустика, гидролокация; системы распознавания речи; сжатие полосы
- 5. Алгоритмы БПФ Быстрое преобразование Фурье (БПФ) – метод вычисления ДПФ АНАЛИЗ И СИНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
- 6. Алгоритм БПФ с прореживанием по времени Пусть N – степень 2. Разобьем {x(n)} на {x1(n)} –
- 7. Алгоритм БПФ с прореживанием по времени Доопределение X(k) для k≥N/2 на основании периодичности N/2 точечных ДПФ:
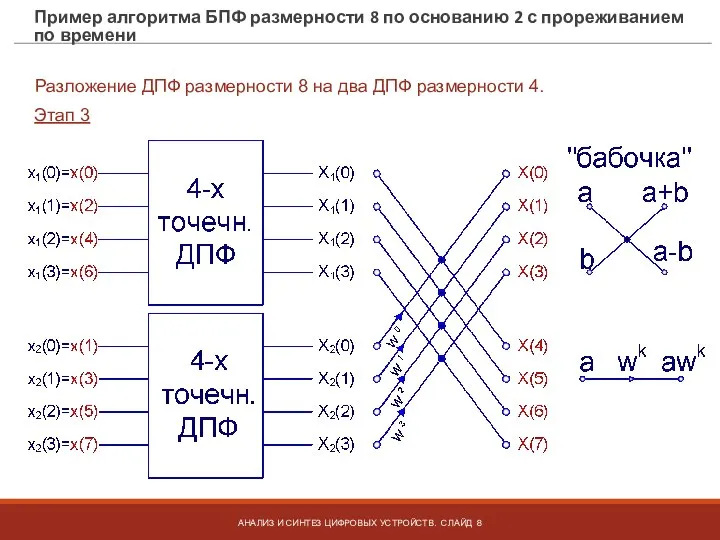
- 8. Пример алгоритма БПФ размерности 8 по основанию 2 с прореживанием по времени АНАЛИЗ И СИНТЕЗ ЦИФРОВЫХ
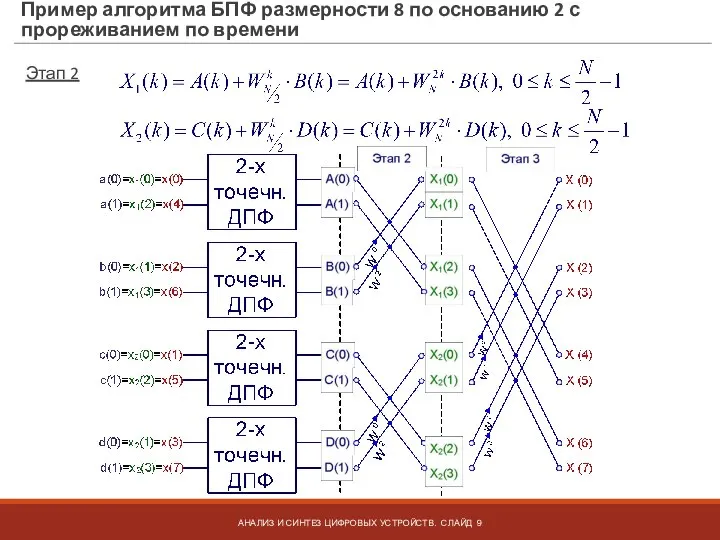
- 9. Пример алгоритма БПФ размерности 8 по основанию 2 с прореживанием по времени Этап 2 АНАЛИЗ И
- 10. Направленный граф алгоритма БПФ размерности N = 8 по основанию 2 с прореживанием по времени и
- 11. Свойства алгоритма БПФ по основанию 2 1. Алгоритм состоит из этапов. На каждом этапе происходит изменение
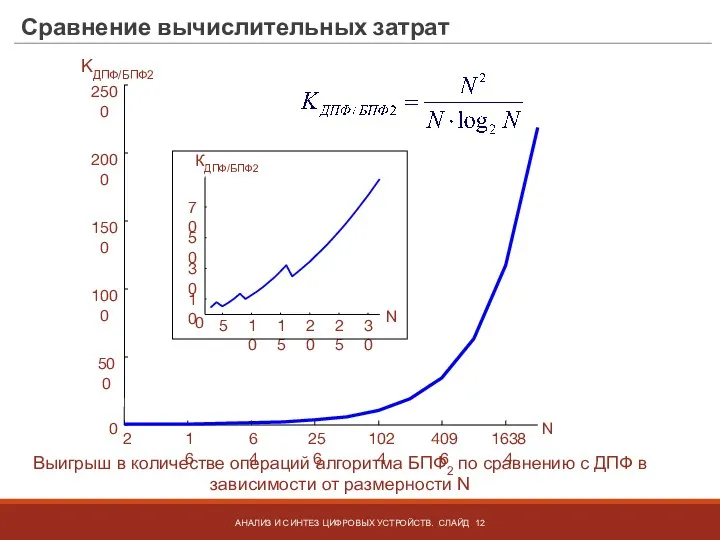
- 12. Сравнение вычислительных затрат АНАЛИЗ И СИНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Выигрыш в количестве операций алгоритма БПФ2 по
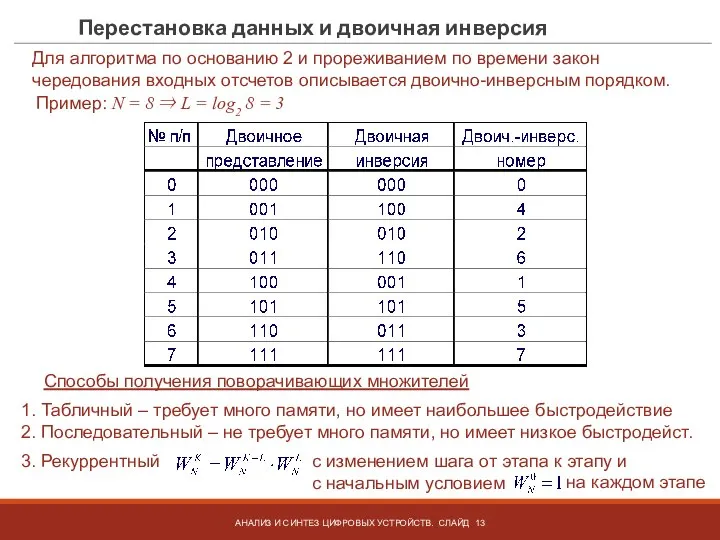
- 13. Перестановка данных и двоичная инверсия АНАЛИЗ И СИНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Для алгоритма по основанию 2
- 14. Алгоритм БПФ с прореживанием по частоте АНАЛИЗ И СИНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Входная последовательность разбивается на
- 15. Алгоритм БПФ с прореживанием по частоте АНАЛИЗ И СИНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Поскольку то X(k) для
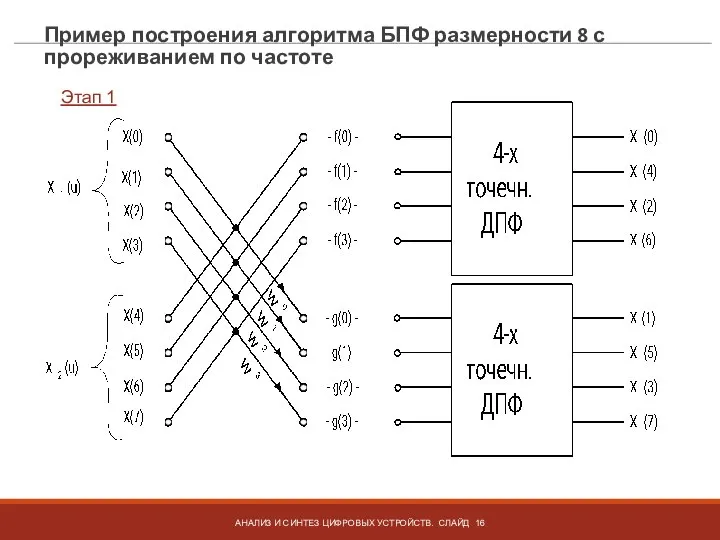
- 16. Пример построения алгоритма БПФ размерности 8 с прореживанием по частоте АНАЛИЗ И СИНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
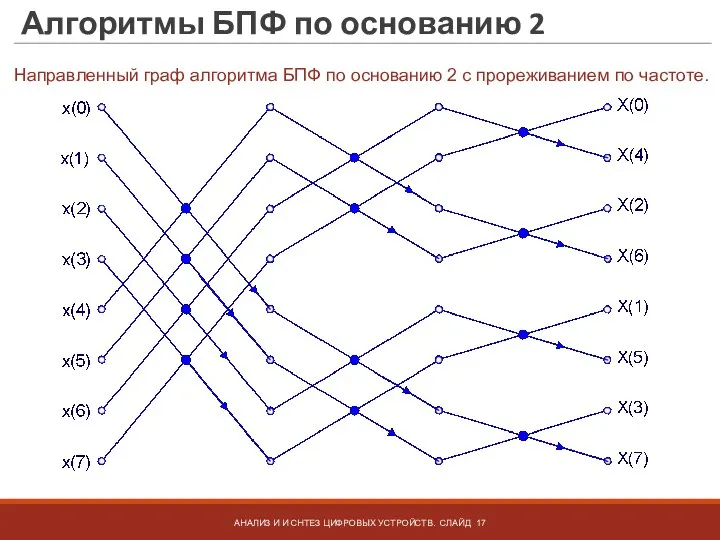
- 17. Алгоритмы БПФ по основанию 2 АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Направленный граф алгоритма БПФ
- 18. Различия алгоритмов БПФ с прореживанием по времени и по частоте АНАЛИЗ И СИНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
- 19. Вычисление обратного ДПФ по алгоритму прямого АНАЛИЗ И СИНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД - обратное ДПФ *
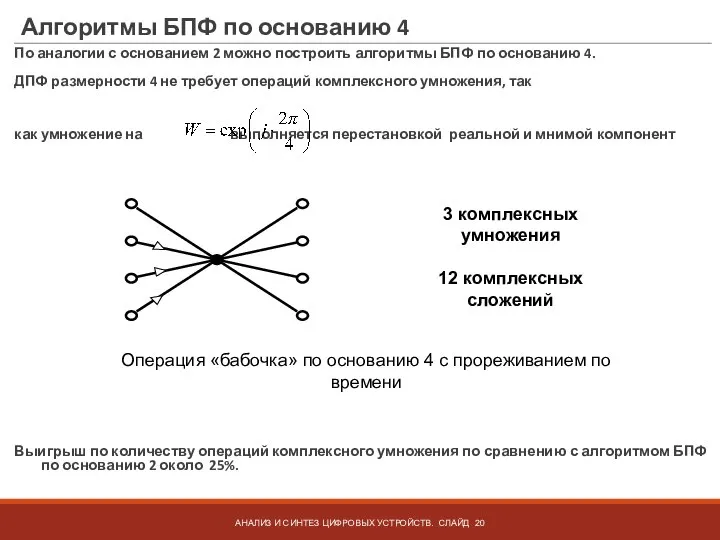
- 20. Алгоритмы БПФ по основанию 4 По аналогии с основанием 2 можно построить алгоритмы БПФ по основанию
- 21. Алгоритм БПФ по основанию 4 размерности 16 АНАЛИЗ И СИНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД 0 4 8
- 22. Принцип построения алгоритма БПФ с произвольным основанием Если N – составное число, то одномерный массив отсчетов
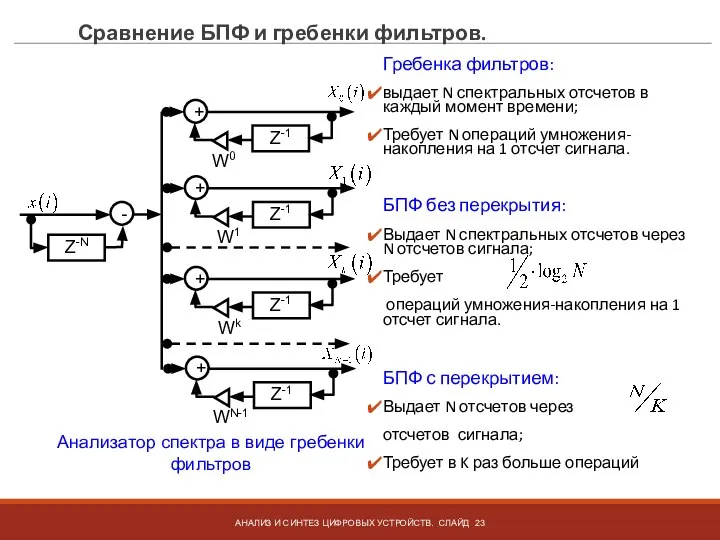
- 23. Сравнение БПФ и гребенки фильтров. Гребенка фильтров: выдает N спектральных отсчетов в каждый момент времени; Требует
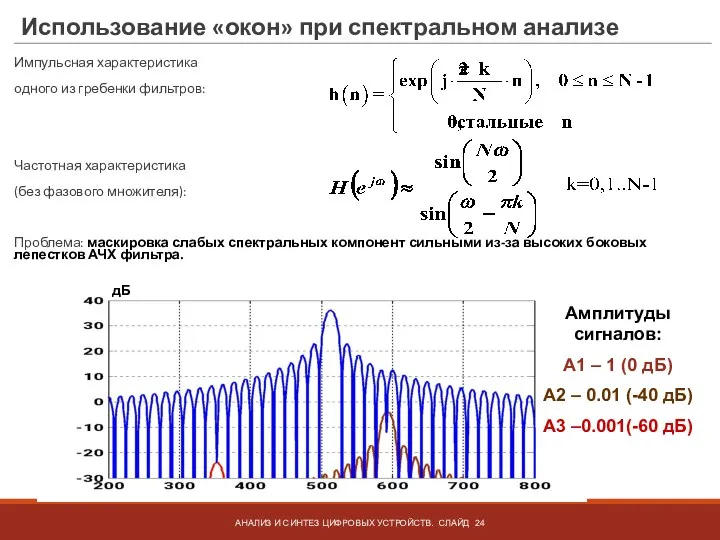
- 24. Использование «окон» при спектральном анализе Импульсная характеристика одного из гребенки фильтров: Частотная характеристика (без фазового множителя):
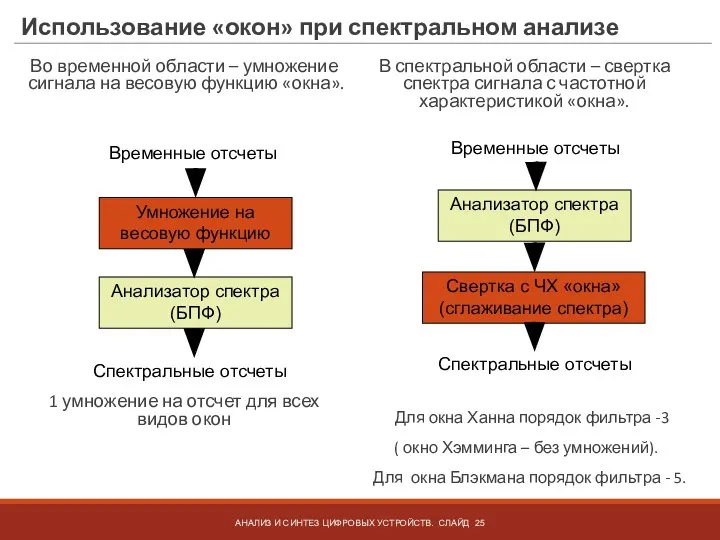
- 25. Использование «окон» при спектральном анализе Во временной области – умножение сигнала на весовую функцию «окна». 1
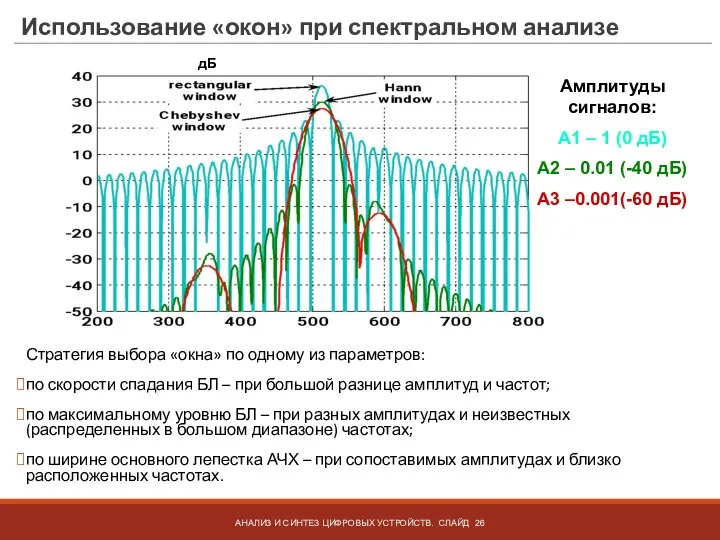
- 26. Использование «окон» при спектральном анализе Стратегия выбора «окна» по одному из параметров: по скорости спадания БЛ
- 27. Классические методы спектрального оценивания Задача: получить оценку спектральной плотности мощности сигнала с минимальной среднеквадратической ошибкой по
- 28. Классические методы спектрального оценивания Особенность оценки СПМ при наличии шума: При увеличении размерности БПФ ошибка оценки
- 29. Периодограммный метод оценки СПМ Последовательность операций: Реализация процесса длиной L отсчетов разбивается на M сегментов размером
- 30. Коррелограммный метод оценки СПМ Основан на дискретном аналоге теоремы Винера-Хинчина. Последовательность операций: Вычислить АКФ реализации процесса
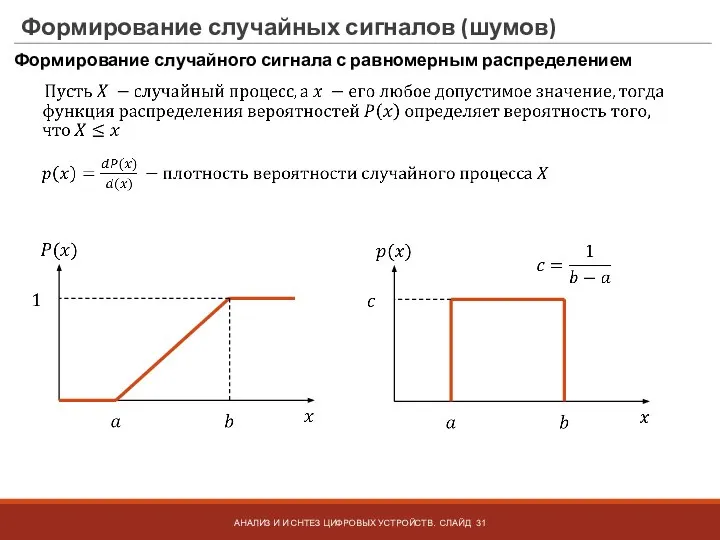
- 31. Формирование случайных сигналов (шумов) Формирование случайного сигнала с равномерным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ.
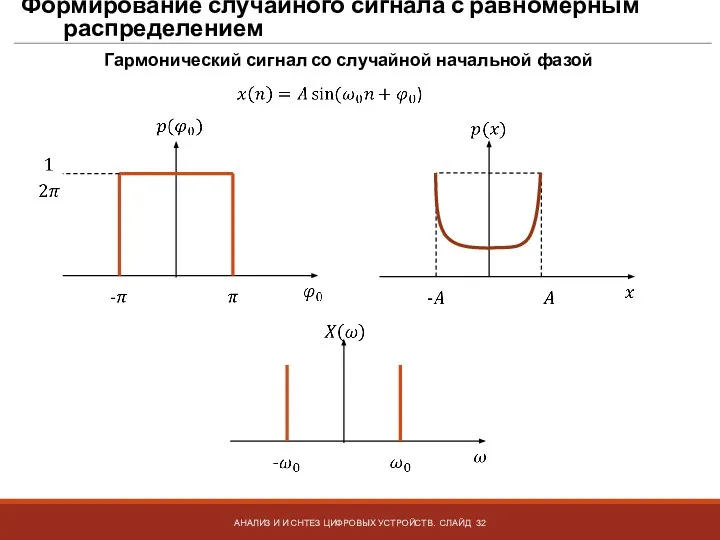
- 32. Формирование случайного сигнала с равномерным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Гармонический сигнал со
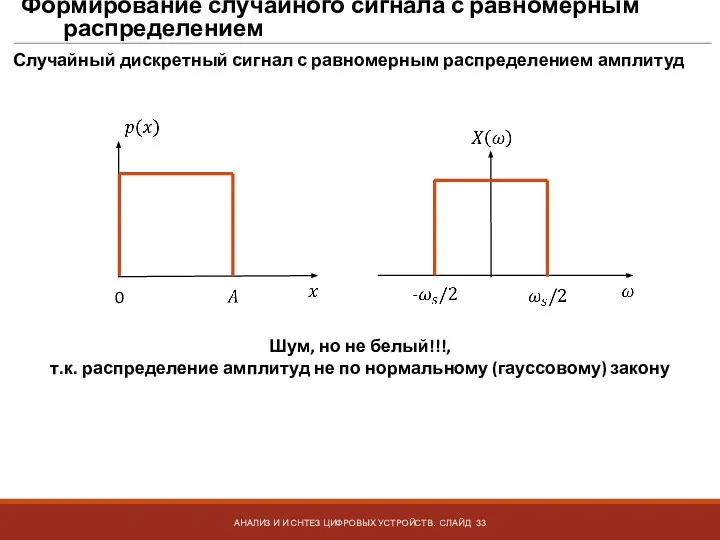
- 33. Формирование случайного сигнала с равномерным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Случайный дискретный сигнал
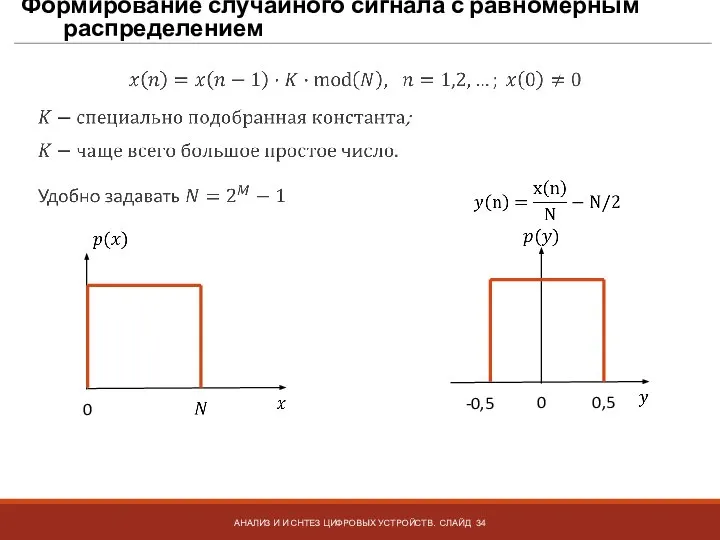
- 34. Формирование случайного сигнала с равномерным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
- 35. Формирование случайного сигнала с равномерным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД М-последовательность или последовательность
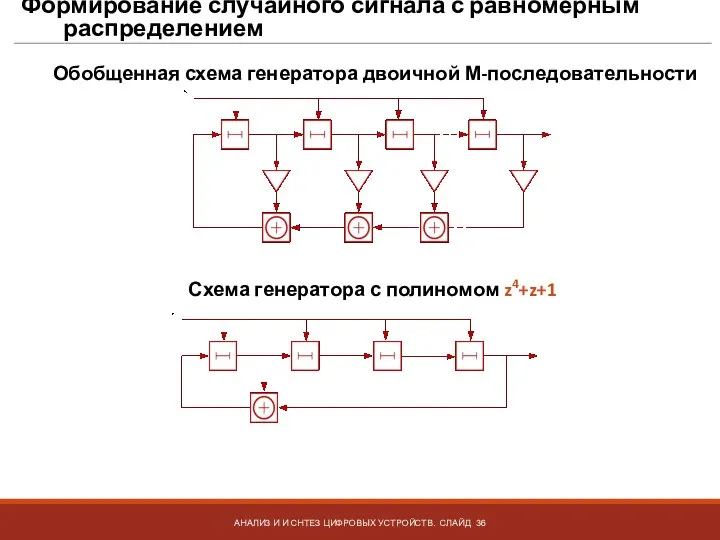
- 36. Формирование случайного сигнала с равномерным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Обобщенная схема генератора
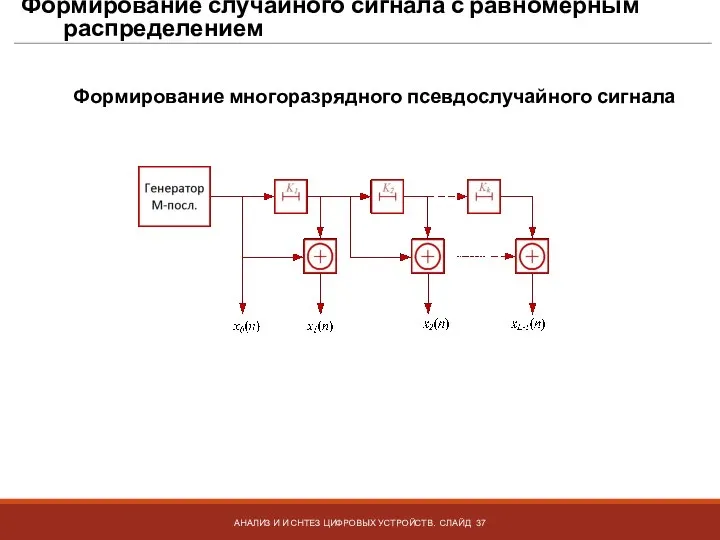
- 37. Формирование случайного сигнала с равномерным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Формирование многоразрядного псевдослучайного
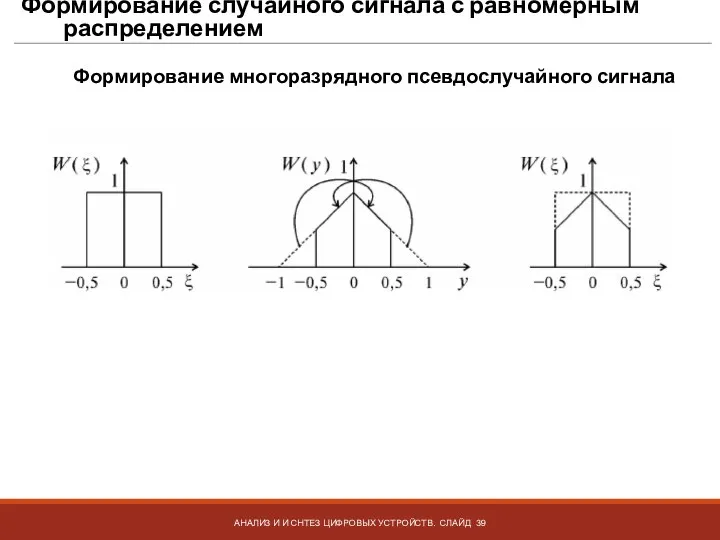
- 38. Формирование случайного сигнала с равномерным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Формирование многоразрядного псевдослучайного
- 39. Формирование случайного сигнала с равномерным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Формирование многоразрядного псевдослучайного
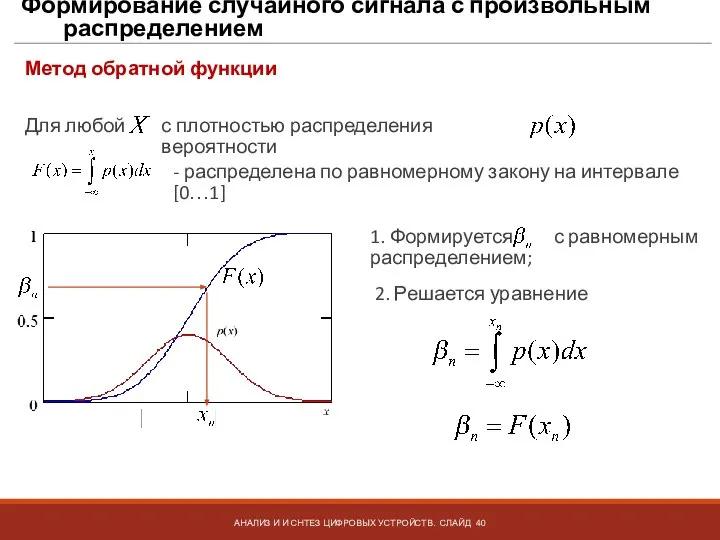
- 40. Формирование случайного сигнала с произвольным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Для любой с
- 41. Формирование случайного сигнала с произвольным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Формирование сигнала с
- 42. Формирование случайного сигнала с нормальным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Формирование сигнала суммированием
- 43. Формирование случайного сигнала с нормальным распределением АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Формирование методом полярных
- 44. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Применяется в микроконтроллерах и ПЛИС, когда операции
- 45. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Основная идея – последовательное (итерационное) приближение аргумента
- 46. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Таким образом, если произвольный угол представить в
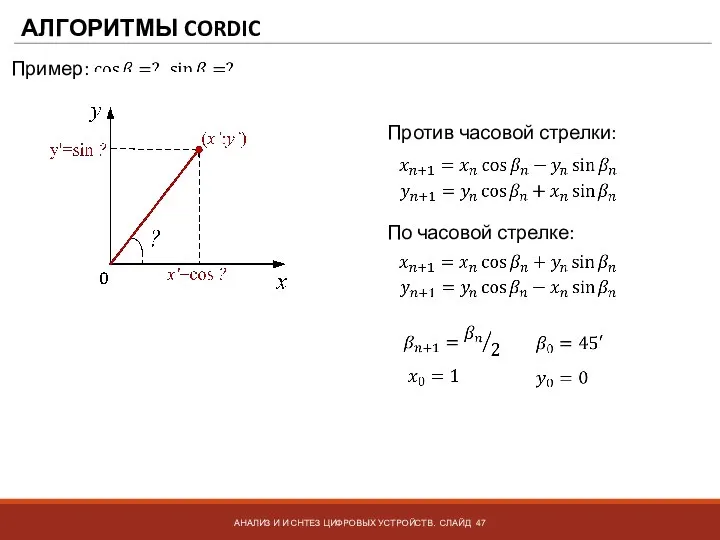
- 47. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Пример: Против часовой стрелки: По часовой стрелке:
- 48. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Пример: => против часовой стрелки Против часовой
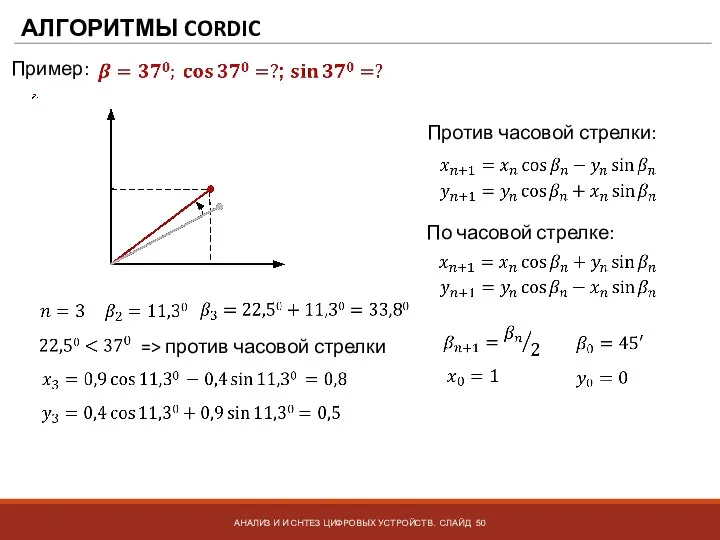
- 49. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Пример: => по часовой стрелке Против часовой
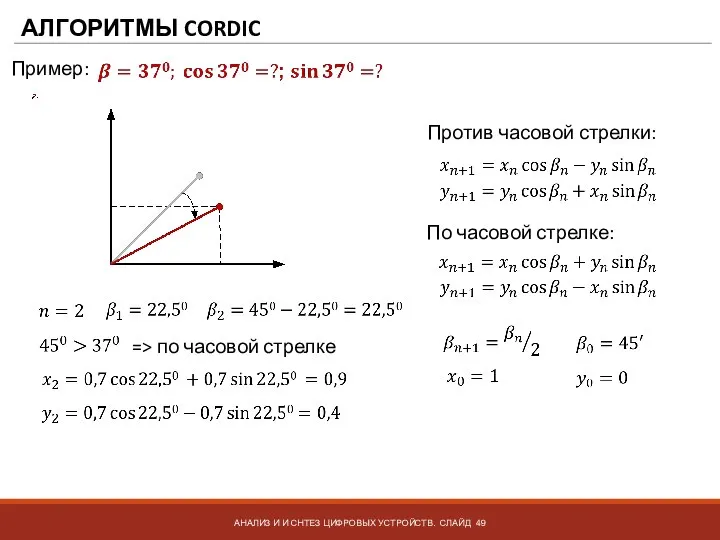
- 50. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Пример: Против часовой стрелки: По часовой стрелке:
- 51. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Пример: Против часовой стрелки: По часовой стрелке:
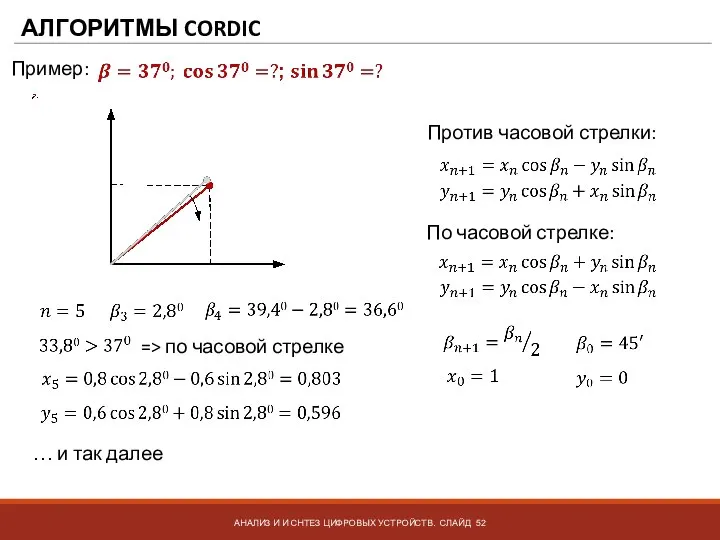
- 52. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Пример: Против часовой стрелки: По часовой стрелке:
- 53. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД значения функции sin и cos возможно вычислить
- 54. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД => Тогда: - коэффициент деформации, на который
- 55. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД => Тогда: - коэффициент деформации, на который
- 56. АЛГОРИТМЫ CORDIC АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД AngTable = 45, 26.565, 14.036, 7.125, 3.576,
- 57. Построение цифровых приёмных устройств АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Цифровое гетеродинирование Назначение: перенос спектра
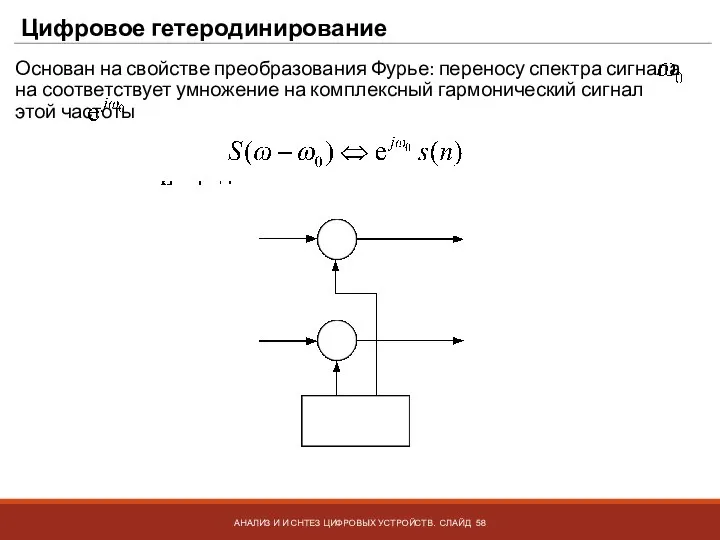
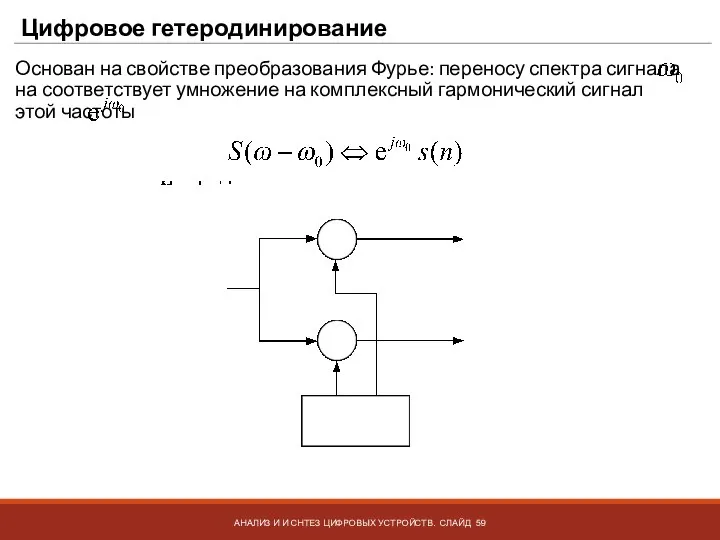
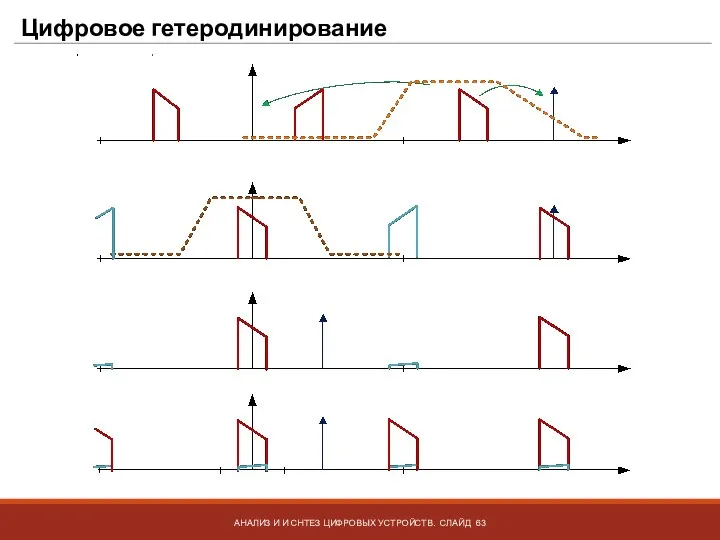
- 58. Цифровое гетеродинирование АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Основан на свойстве преобразования Фурье: переносу спектра
- 59. Цифровое гетеродинирование АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Основан на свойстве преобразования Фурье: переносу спектра
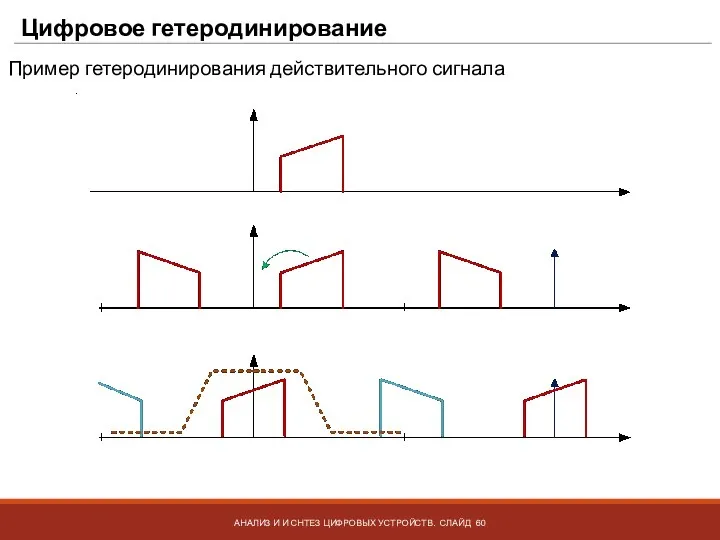
- 60. Цифровое гетеродинирование АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Пример гетеродинирования действительного сигнала
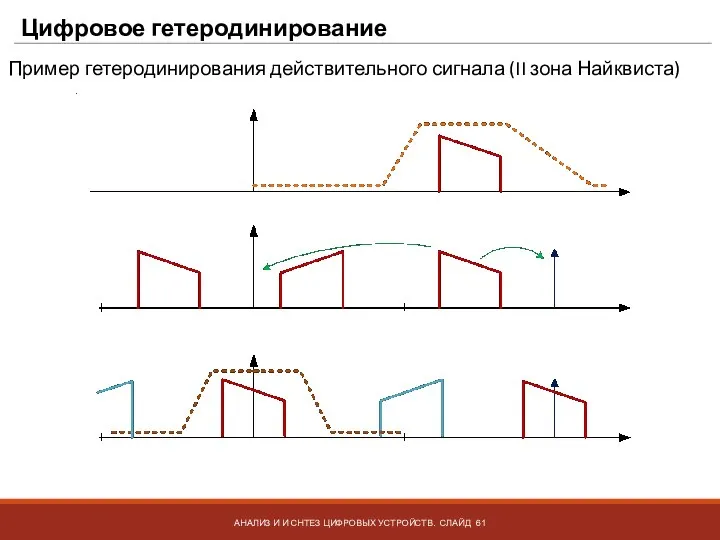
- 61. Цифровое гетеродинирование АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Пример гетеродинирования действительного сигнала (II зона Найквиста)
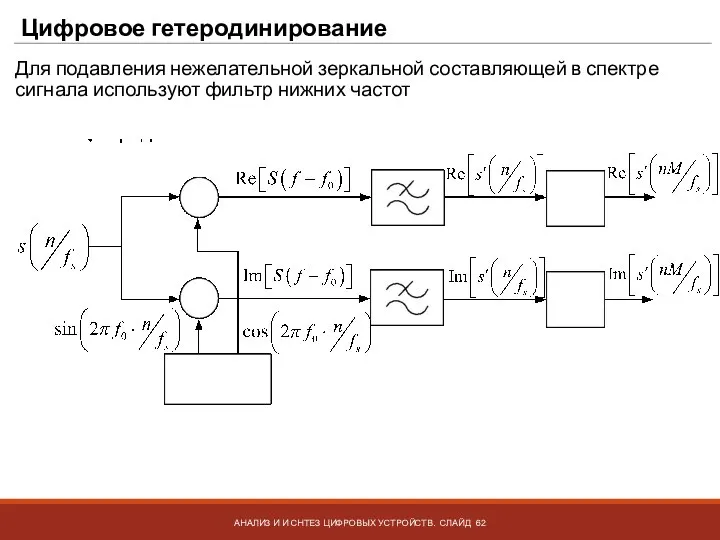
- 62. Цифровое гетеродинирование АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Для подавления нежелательной зеркальной составляющей в спектре
- 63. Цифровое гетеродинирование АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
- 64. Прямой цифровой синтез Методы синтеза частоты: прямой цифровой синтез (Direct Digital Synthesis - DDS) косвенный (на
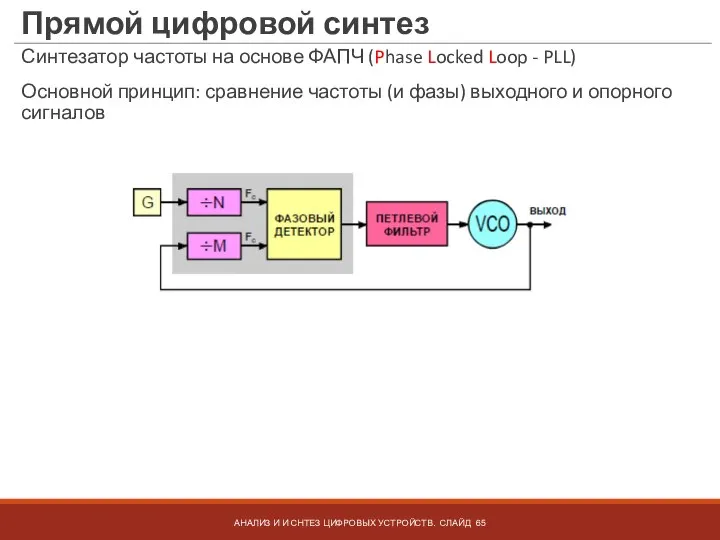
- 65. Прямой цифровой синтез Синтезатор частоты на основе ФАПЧ (Phase Locked Loop - PLL) АНАЛИЗ И И
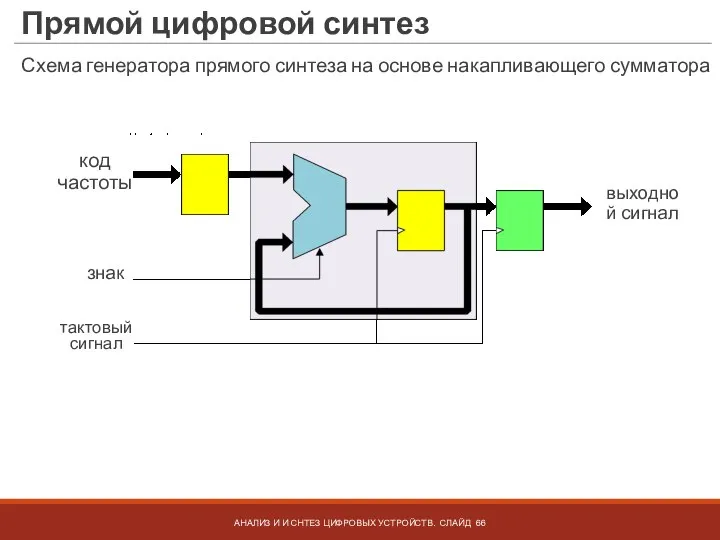
- 66. Прямой цифровой синтез АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД код частоты знак тактовый сигнал выходной
- 67. Прямой цифровой синтез АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД аккумулятор частоты Шаг приращения частоты выходной
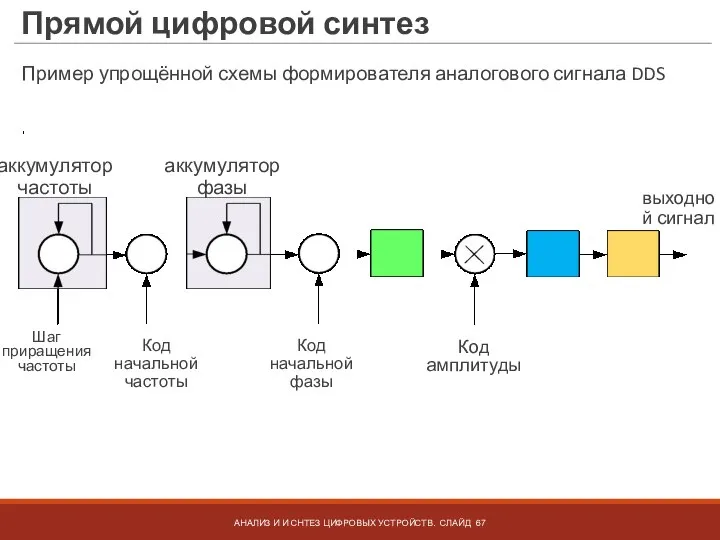
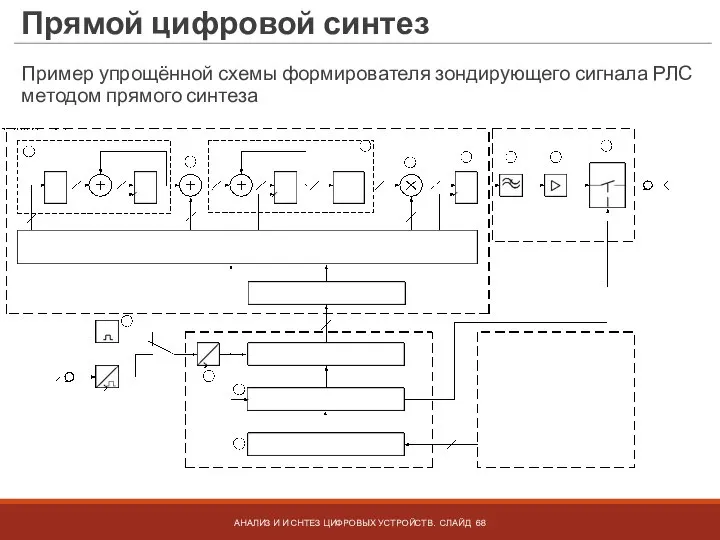
- 68. Прямой цифровой синтез АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Пример упрощённой схемы формирователя зондирующего сигнала
- 69. CIC-фильтры АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Сascaded Integral-Comb filters - каскадные интегрально-гребенчатые фильтры, фильтры
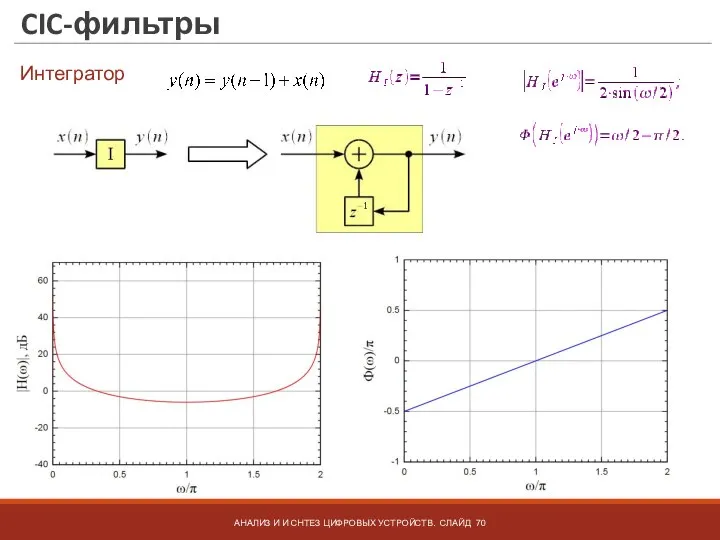
- 70. CIC-фильтры АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Интегратор
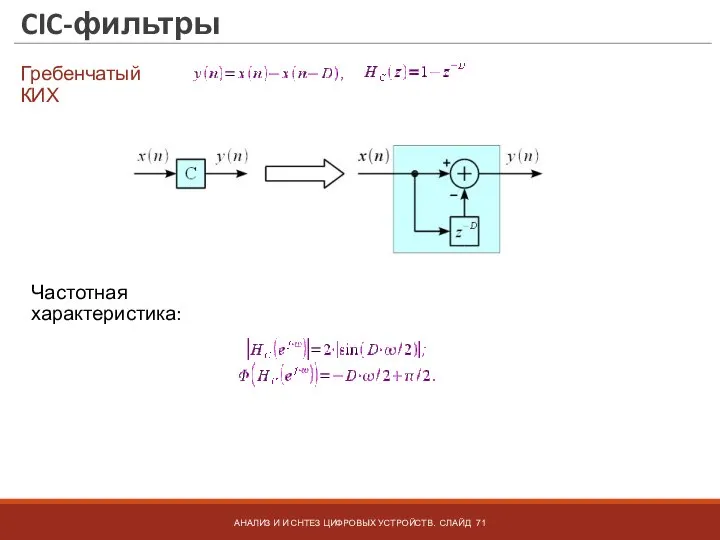
- 71. CIC-фильтры АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Гребенчатый КИХ Частотная характеристика:
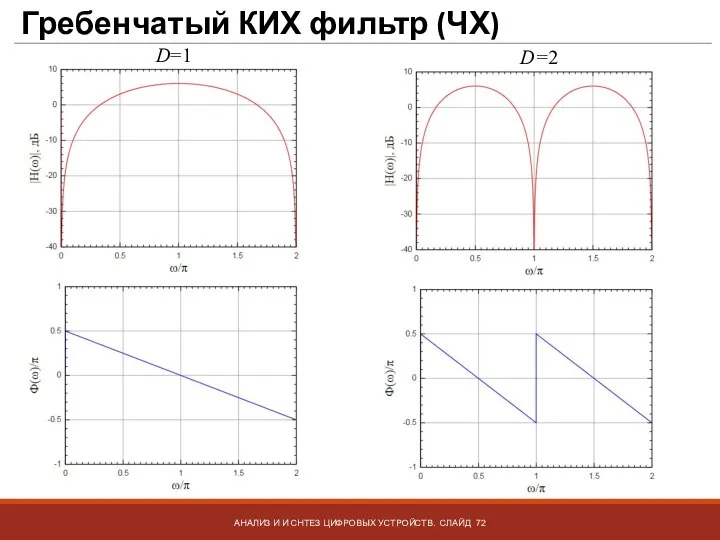
- 72. Гребенчатый КИХ фильтр (ЧХ) АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД D=1 D=2
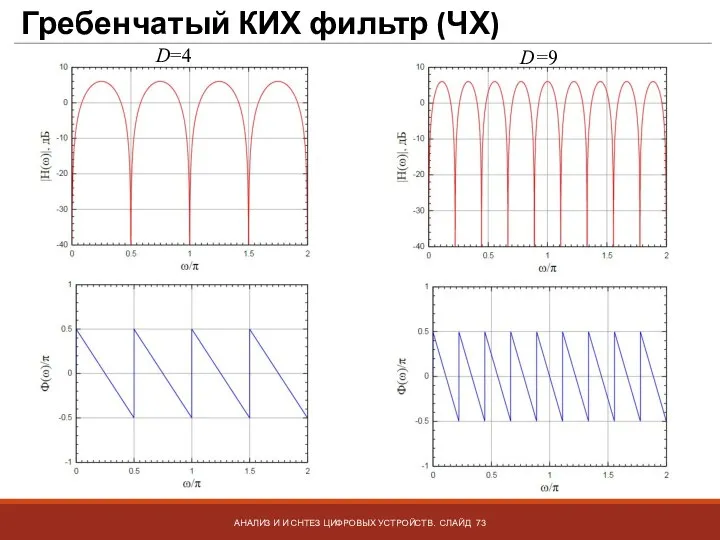
- 73. Гребенчатый КИХ фильтр (ЧХ) АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД D=4 D=9
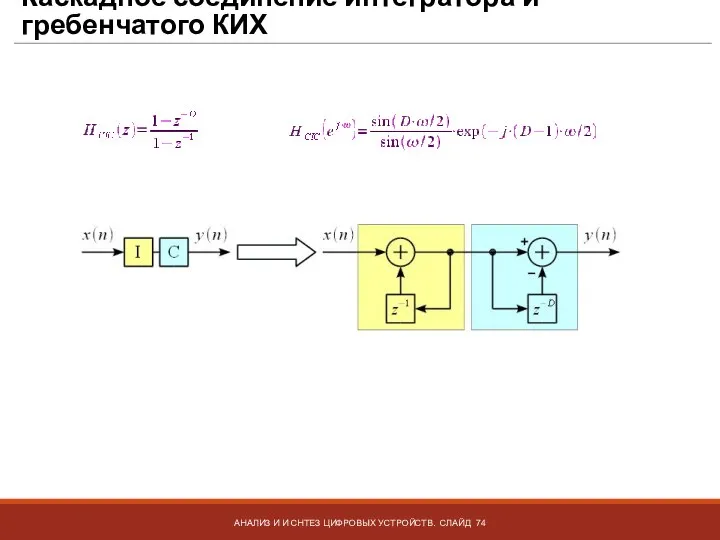
- 74. Каскадное соединение интегратора и гребенчатого КИХ АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
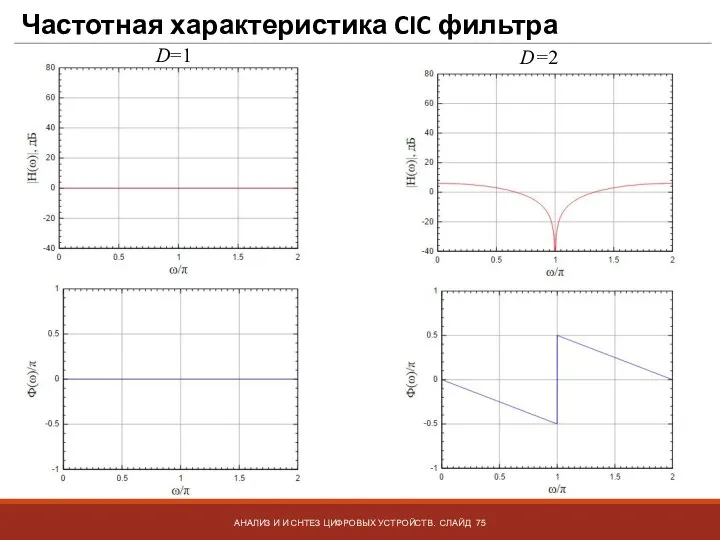
- 75. Частотная характеристика CIC фильтра АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД D=1 D=2
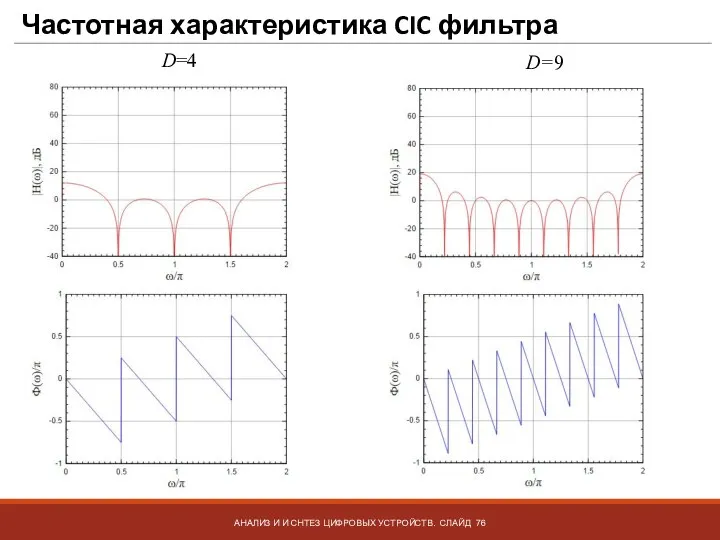
- 76. Частотная характеристика CIC фильтра АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД D=4 D=9
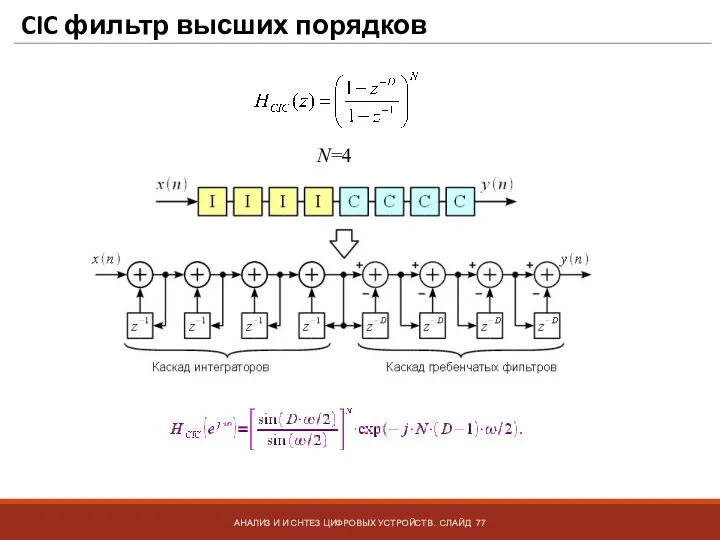
- 77. CIC фильтр высших порядков АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД N=4
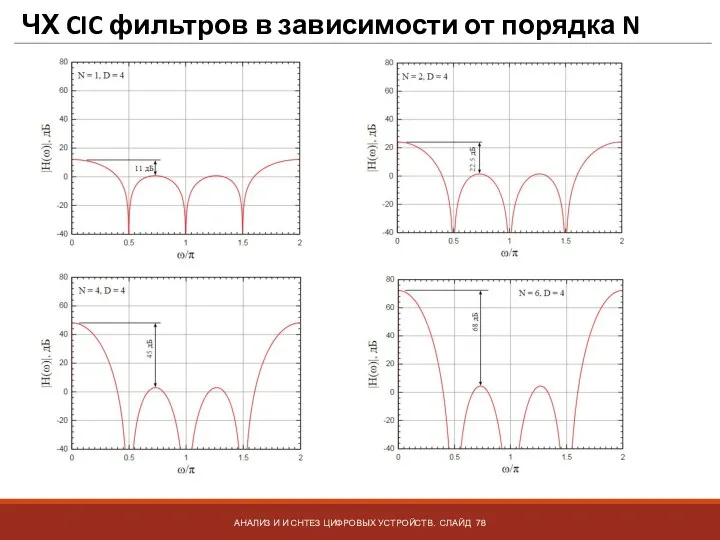
- 78. ЧХ CIC фильтров в зависимости от порядка N АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
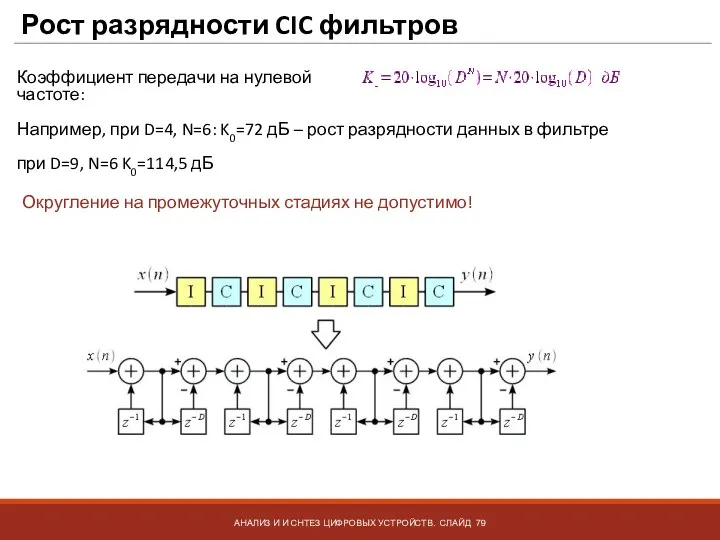
- 79. Рост разрядности CIC фильтров АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Коэффициент передачи на нулевой частоте:
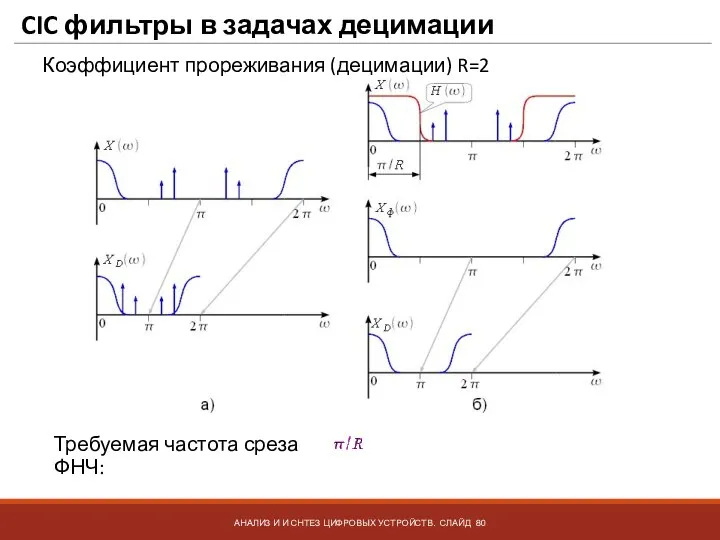
- 80. CIC фильтры в задачах децимации АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Коэффициент прореживания (децимации) R=2
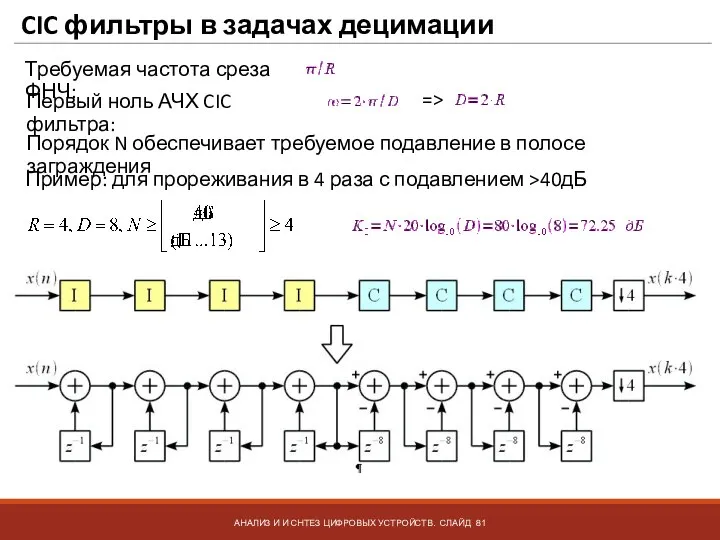
- 81. CIC фильтры в задачах децимации АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Требуемая частота среза ФНЧ:
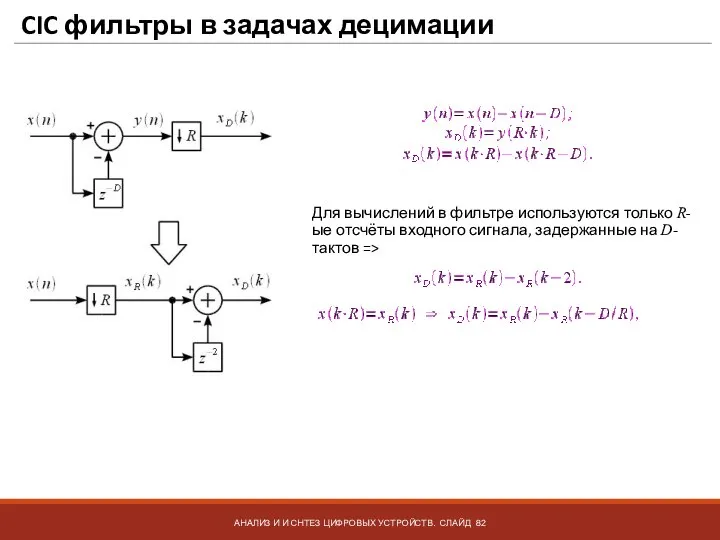
- 82. CIC фильтры в задачах децимации АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Для вычислений в фильтре
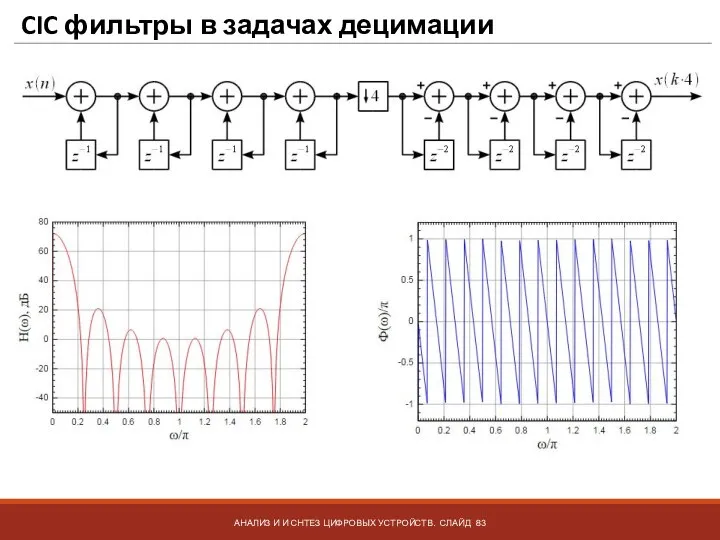
- 83. CIC фильтры в задачах децимации АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
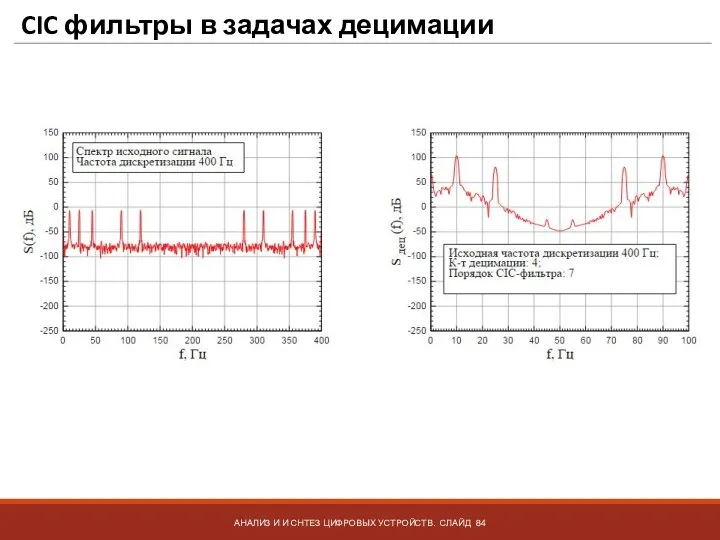
- 84. CIC фильтры в задачах децимации АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
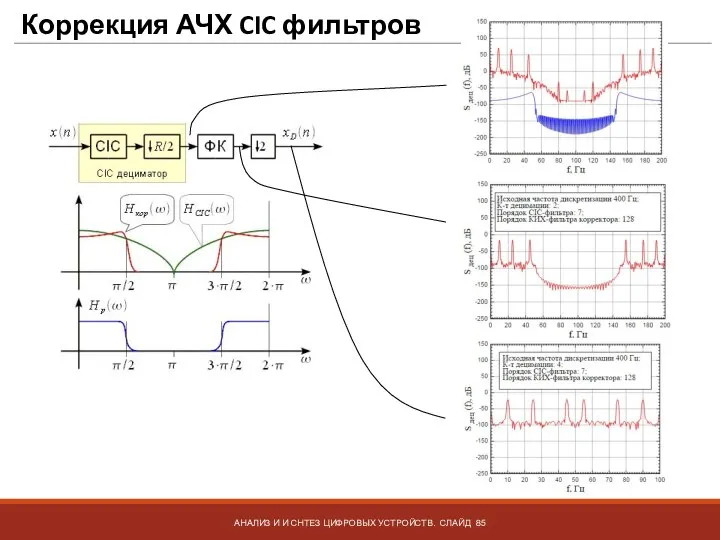
- 85. Коррекция АЧХ CIC фильтров АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
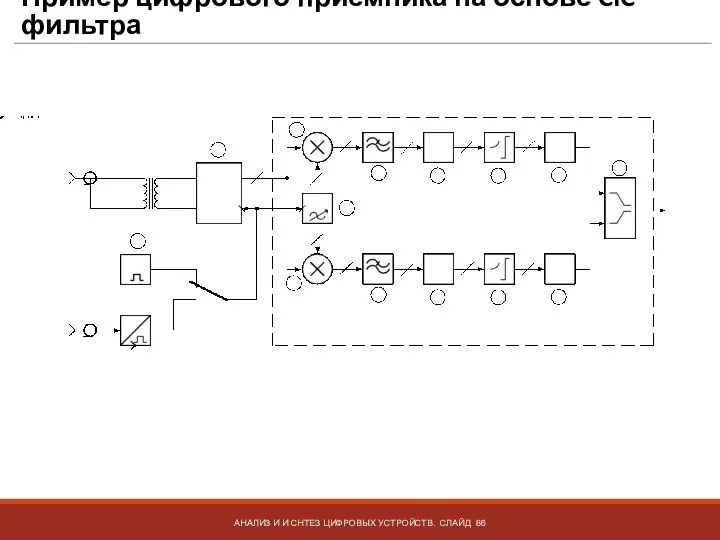
- 86. Пример цифрового приемника на основе CIC фильтра АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
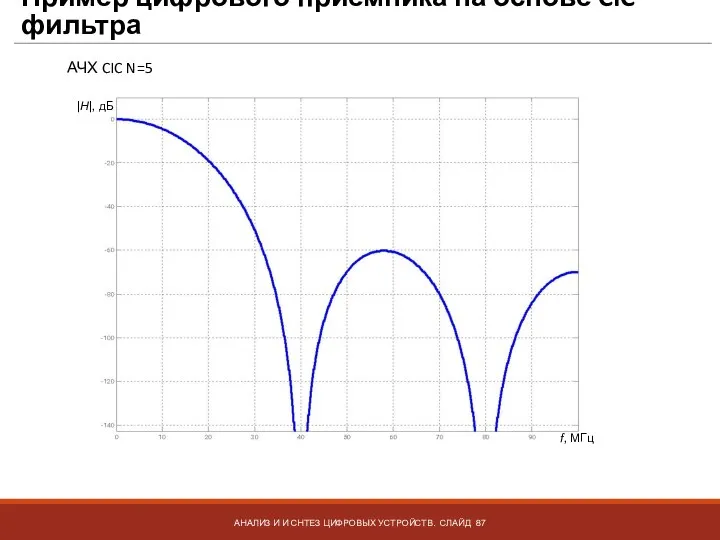
- 87. Пример цифрового приемника на основе CIC фильтра АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД АЧХ CIC
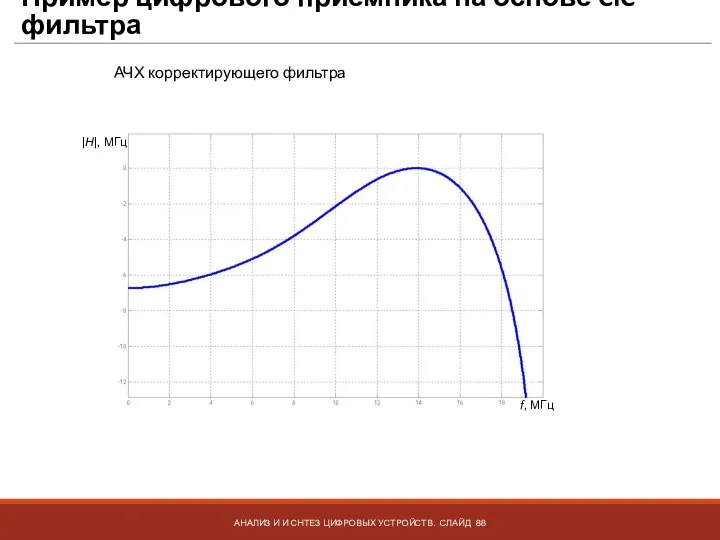
- 88. Пример цифрового приемника на основе CIC фильтра АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД АЧХ корректирующего
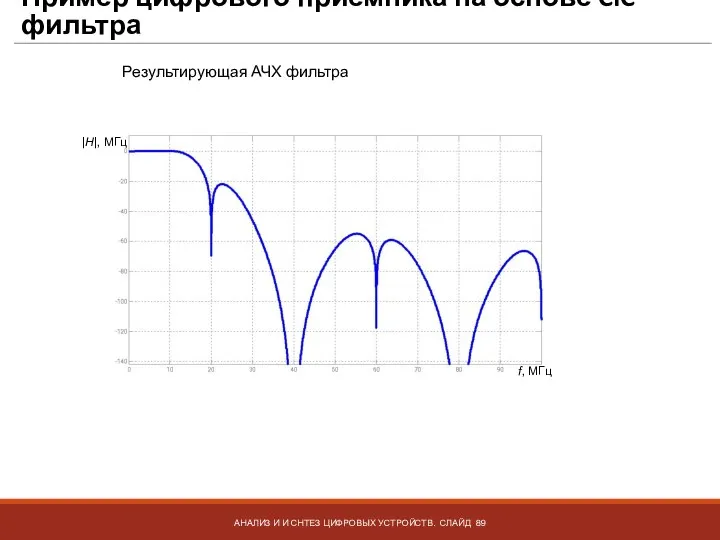
- 89. Пример цифрового приемника на основе CIC фильтра АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД Результирующая АЧХ
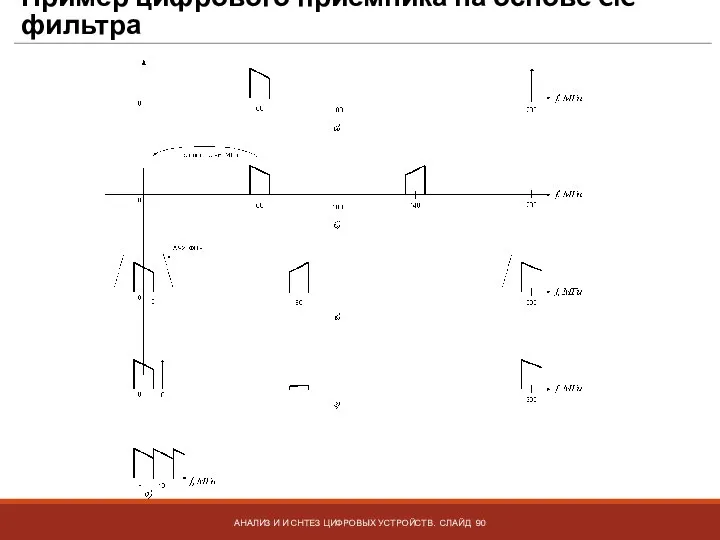
- 90. Пример цифрового приемника на основе CIC фильтра АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД
- 91. Полуполосные фильтры АНАЛИЗ И И СНТЕЗ ЦИФРОВЫХ УСТРОЙСТВ. СЛАЙД half band filters – экономичные фильтры, которые
- 93. Скачать презентацию




































 куала
куала Цифровые образовательные ресурсы и модели их использования в образовательном процессе А. Л. Семенов.
Цифровые образовательные ресурсы и модели их использования в образовательном процессе А. Л. Семенов. Методологические основы технологизации Классификация технологий
Методологические основы технологизации Классификация технологий Основы ПЦР-анализа
Основы ПЦР-анализа Презентация1
Презентация1 Образ учителя
Образ учителя Виды складок. Обработка складок
Виды складок. Обработка складок Презентация на тему Все народы воспевают материнство (4 класс)
Презентация на тему Все народы воспевают материнство (4 класс) Уникальность бренда
Уникальность бренда Презентация «История жизни М.Акмуллы»
Презентация «История жизни М.Акмуллы» Финансовое планирование и контроль на предприятии
Финансовое планирование и контроль на предприятии Инструкция по вымачиванию дубовых бочек
Инструкция по вымачиванию дубовых бочек Тициан Вечеллио ди Кадоре
Тициан Вечеллио ди Кадоре Cell cycle control
Cell cycle control Моя конвенция
Моя конвенция Реализация проекта по персонифицированному финансированию дополнительного образования детей
Реализация проекта по персонифицированному финансированию дополнительного образования детей Комбинированный тур по Байкалу
Комбинированный тур по Байкалу С днем независимости, Казахстан
С днем независимости, Казахстан Витамин В2
Витамин В2 Проектный менеджмент. Фандрайзинг. Введение в курс
Проектный менеджмент. Фандрайзинг. Введение в курс Права и обязанности граждан
Права и обязанности граждан Социальная защита рабочих на производстве
Социальная защита рабочих на производстве Новые преобразователи частоты CombiVario
Новые преобразователи частоты CombiVario Военно-патриотический музей «ПОИСК»
Военно-патриотический музей «ПОИСК»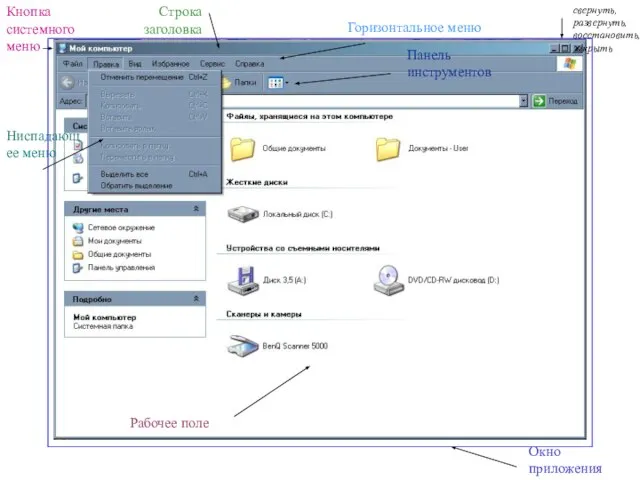 Строка заголовка
Строка заголовка Твой выбор. Виды спорта. Тренера
Твой выбор. Виды спорта. Тренера Операционные системы Управление виртуальной памятью в Win 32
Операционные системы Управление виртуальной памятью в Win 32  Общие положения и руководящие принципы составления плана тренировки
Общие положения и руководящие принципы составления плана тренировки