Метрико-топологические вычисления в конструктивном мире кубических структур.

Введение.
Парадигма «физика-топология-логика-компьютерные вычисления-Розеттский камень».Формально-языковые связки «физика-топология», «топология-логика-компьютерные вычисления».
Построение конструктивного мира для решения задач синтеза геометрико-топологических структур компьютерными методами.
Роль кубических структур как удобного материала для алгебраических представлений и для машинных параллельных реализаций .
Влияние на архитектуру компьютеров новых поколений.

Математика и компьютер.
Первая сторона ответственности математиков состоит в том, чтобы, используя опыт и достижения математики, особенно математики ХХ века, значительно расширить возможность создания адекватных языков в других разделах науки… Многое будет сделано, в особенности в век компьютеров, которые медленно, но неизбежно будут менять психологию математиков…
И.М.Гельфанд.

О конструкции многообразия
2-сферы. MITgcm.
MITgcm-модель глобальной циркуляции океан-атмосфера.
Общая схема основана на представлении моделируемого слоя, как мембраны на поверхности планеты в виде 2-сферы.
Гибкость представления при детализации модели обеспечивается различной дискретизацией псевдоквадратного покрытия 2-сферы.
Такая конструкция названа кубоидной конформной сферой.

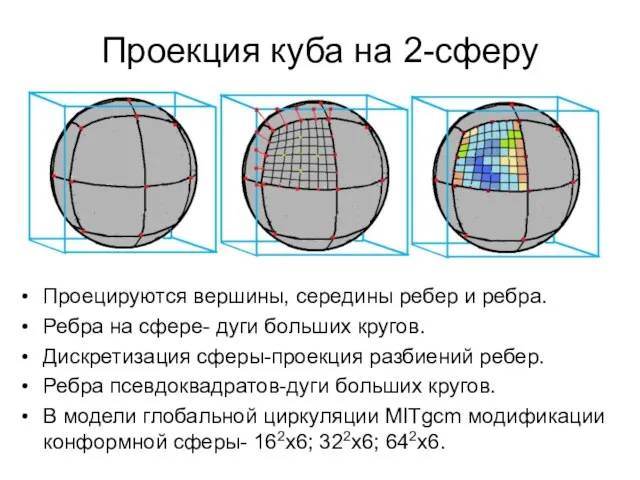
Проекция куба на 2-сферу
Проецируются вершины, середины ребер и ребра.
Ребра на сфере- дуги больших кругов.
Дискретизация сферы-проекция разбиений ребер.
Ребра псевдоквадратов-дуги больших кругов.
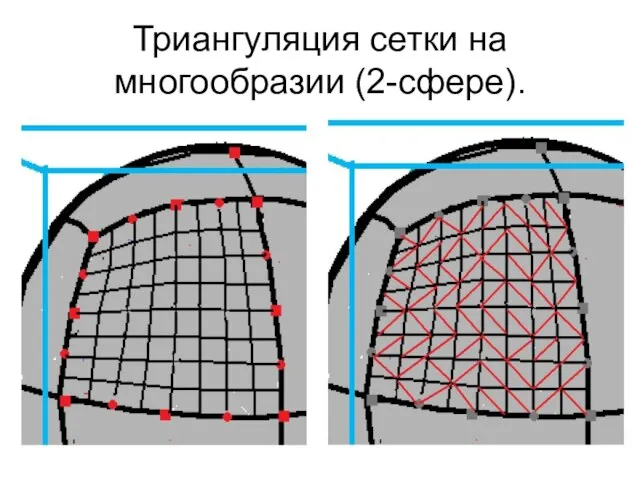
В модели глобальной циркуляции MITgcm модификации конформной сферы- 162х6; 322х6; 642х6.

Триангуляция сетки на многообразии (2-сфере).

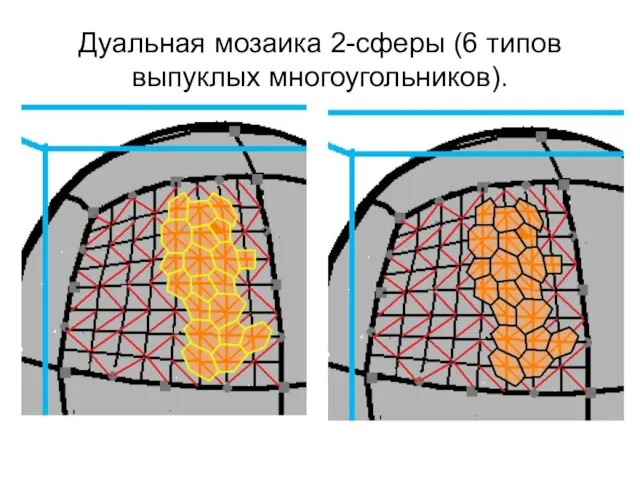
Дуальная мозаика 2-сферы (6 типов выпуклых многоугольников).

Общая схема конструктивного подхода к построению n-сферы.
1.Выбор алфавита и метода кодирования для граней кубической n-окрестности.
2.Описание множества слов, представляющих внешние и внутренние гиперграни.
3.На основании гомеоморфности поверхности n+1-куба и n-сферы вычислить все карты смежности для граней n-сферы.
Спроецировать все целые точки (вершины) n-окрестности на геометрическую (заданную уравнением Σ xi2=1;) cферу.

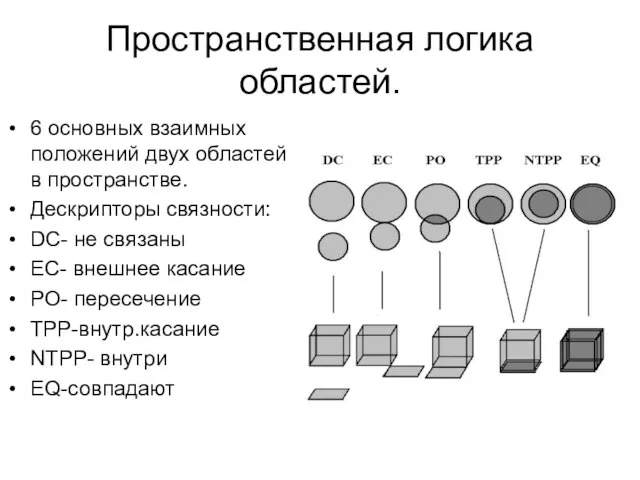
Пространственная логика областей.
6 основных взаимных положений двух областей в пространстве.
Дескрипторы связности:
DC- не связаны
EC- внешнее касание
PO- пересечение
TPP-внутр.касание
NTPP- внутри
EQ-совпадают

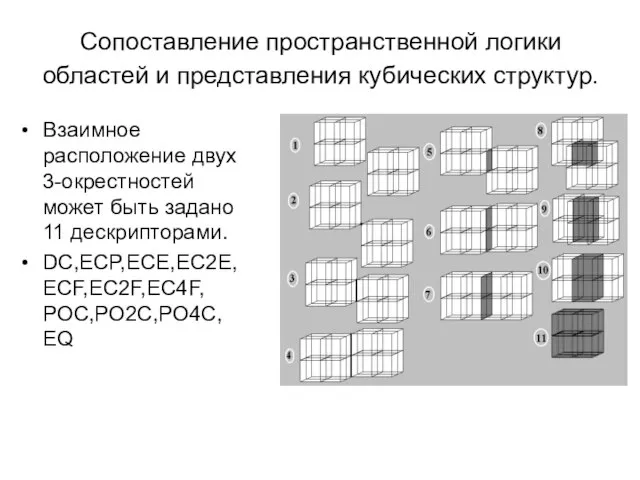
Сопоставление пространственной логики областей и представления кубических структур.
Взаимное расположение двух 3-окрестностей может быть задано 11 дескрипторами.
DC,ECP,ECE,EC2E,ECF,EC2F,EC4F, POC,PO2C,PO4C, EQ

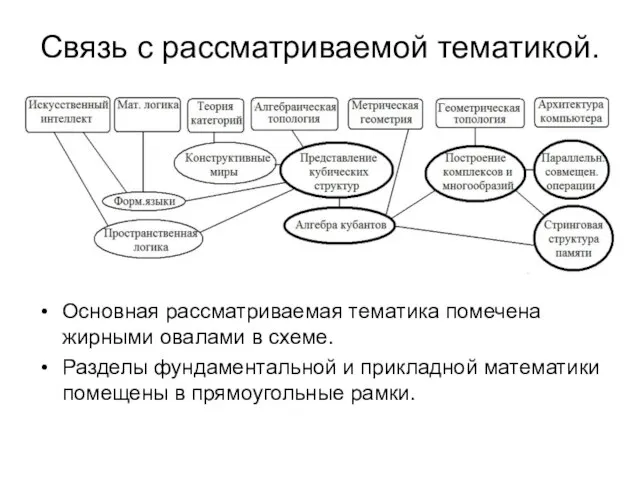
Связь с рассматриваемой тематикой.
Основная рассматриваемая тематика помечена жирными овалами в схеме.
Разделы фундаментальной и прикладной математики помещены в прямоугольные рамки.

Основы представления кубических структур.

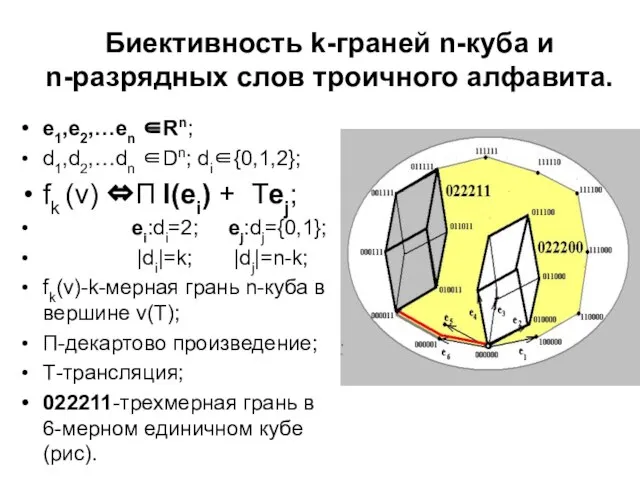
Биективность k-граней n-куба и
n-разрядных слов троичного алфавита.
е1,е2,…еn ∈Rn;
d1,d2,…dn ∈Dn; di∈{0,1,2};
fk (v) ⇔П I(ei) + Tej;
ei:di=2; ej:dj={0,1};
|di|=k; |dj|=n-k;
fk(v)-k-мерная грань n-куба в вершине v(T);
П-декартово произведение;
Т-трансляция;
022211-трехмерная грань в 6-мерном единичном кубе (рис).

Определение кубанта и умножения.
Кубант (кубический квант)- n-разрядное троичное слово, биективное k-мерной грани (k=0-n) n-мерного единичного куба (n-куба). Алфавит {0;1;2}
На кубантах задана бинарная операция «умножение» с расширением алфавита до {Ø;0;1;2}:
Правила поразрядного коммутативного умножения:
0⊗0=0; 0⊗1=1⊗0=Ø; 0⊗2=2⊗0=0; 1⊗2=2⊗1=1; 2⊗2=2; Ø,0,1,2xØ=Ø;
В префиксной форме П(201221;211122)=2Ø1121; (эти 3-грани в 6-кубе не пересекаются и Lmin=1);

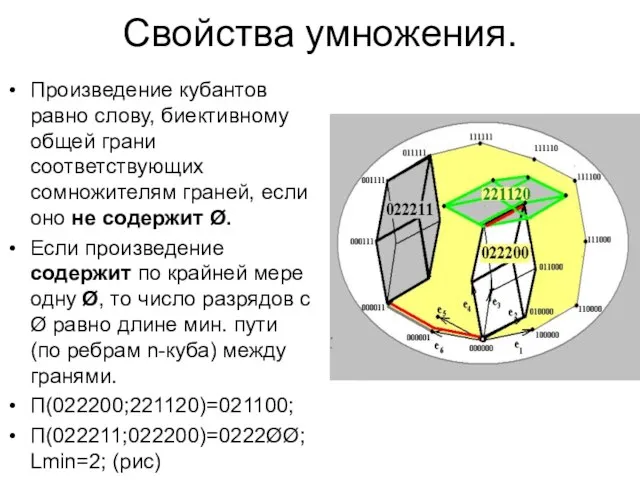
Свойства умножения.
Произведение кубантов равно слову, биективному общей грани соответствующих сомножителям граней, если оно не содержит Ø.
Если произведение содержит по крайней мере одну Ø, то число разрядов с Ø равно длине мин. пути (по ребрам n-куба) между гранями.
П(022200;221120)=021100;
П(022211;022200)=0222ØØ; Lmin=2; (рис)

Моноид кубантов и псевдокубантов
Определение. Псевдокубант n-разрядное четверичное слово (алфавит {Ø,0,1,2} по крайней мере с одним из разрядов Ø.
При заданном умножении множество всех n-разрядных четверичных слов (алфавит {Ø,0,1,2}), кубанты и псевдокубанты, образуют моноид с единицей – кубант 22…2 (весь n-куб).
Общее число мономов 4n, среди них кубантов 3n.

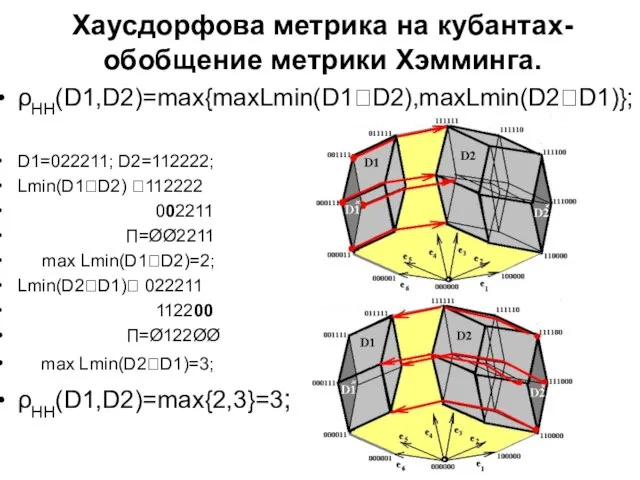
Хаусдорфова метрика на кубантах- обобщение метрики Хэмминга.
ρHH(D1,D2)=max{maxLmin(D1?D2),maxLmin(D2?D1)};
D1=022211; D2=112222;
Lmin(D1?D2) ?112222
002211
П=ØØ2211
max Lmin(D1?D2)=2;
Lmin(D2?D1)? 022211
112200
П=Ø122ØØ
max Lmin(D2?D1)=3;
ρHH(D1,D2)=max{2,3}=3;

Дескриптивное описание алгоритма вычисления НН-расстояния между гранями n-куба
Пусть граням n-куба f1 и f2 соответствуют кубанты D1=d11,…d1n; D2=d21,…d2n;
1.Вычисление max Lmin(D1?D2): рассматриваются все пары разрядов d1i и d2i (i=1-n).Если d1i=2, а d2i=0, то d1i заменяется на 1; если d1i=2, а d2i=1, то замена d1i на 0. В остальных случаях замен нет. D1 c заменами обозначим D1*. Затем вычисляется произведение П(D1*,D2) и в нем подсчитывается число разрядов с Ø, которое и равно max Lmin(D1?D2).
2.Вычисление max Lmin(D2?D1) происходит идентично пункту 1. с заменой индекса 1 на 2 и 2 на1.
3. Из двух величин max Lmin(D1?D2), max Lmin(D2?D1) (целые, неотрицательные числа) выбирается максимальное, которое и равно ρНН(D1,D2)=ρHH(f1,f2).

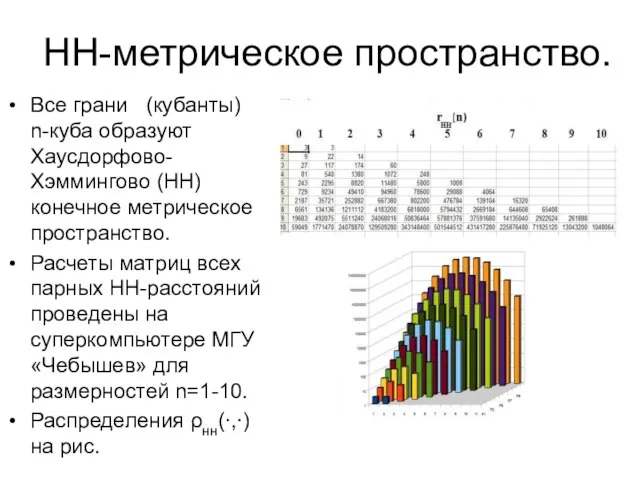
НН-метрическое пространство.
Все грани (кубанты) n-куба образуют Хаусдорфово-Хэммингово (НН) конечное метрическое пространство.
Расчеты матриц всех парных НН-расстояний проведены на суперкомпьютере МГУ «Чебышев» для размерностей n=1-10.
Распределения ρнн(∙,∙) на рис.

Расширение понятий и операций.
Путь размерности k (k-путь) между k-гранями f1 и f2- последовательность граней вида f11,f12,…f1s, где все k-грани; f11=f1;f1s=f2; и для i=1-s выполнено f1i∩f1i+1= грани размерности k-1;
Биективно: k-путь между кубантами D1 иD2 последовательность D11,D12,…D1s такая, что D11=D1, D1s=D2; все D1i содержат ровно k букв «2»; и для i=1-s выполнено D1i⊗D1i+1=кубант с k-1 буквой «2». Кратчайший k-путь, когда s минимально.
Оператор (унарный) взятия границы(∂D) –множество кубантов, биективное гиперграням соответствующего куба.
Оператор (m-арный) выпуклой оболочки (соnv{D1,…Dm}) – кубант минимальной размерности D0: {D1,…Dm} ⊆ D0;

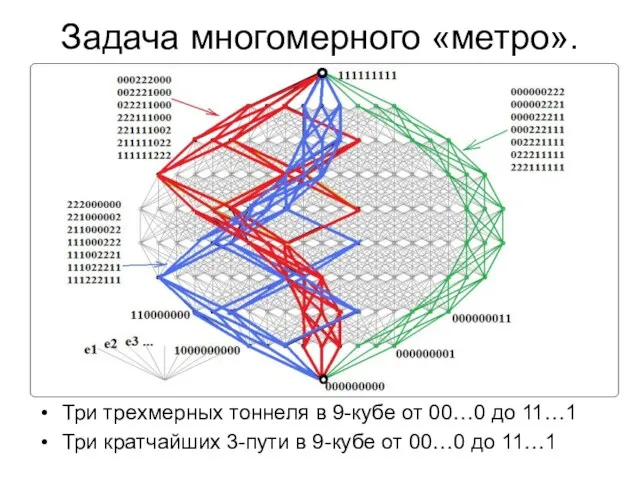
Задача многомерного «метро».
Три трехмерных тоннеля в 9-кубе от 00…0 до 11…1
Три кратчайших 3-пути в 9-кубе от 00…0 до 11…1

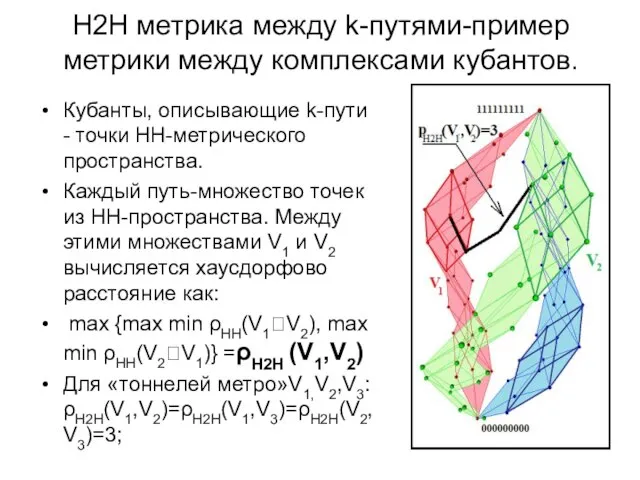
Н2H метрика между k-путями-пример метрики между комплексами кубантов.
Кубанты, описывающие k-пути - точки НН-метрического пространства.
Каждый путь-множество точек из НН-пространства. Между этими множествами V1 и V2 вычисляется хаусдорфово расстояние как:
max {max min ρHH(V1?V2), max min ρHH(V2?V1)} =ρH2H (V1,V2)
Для «тоннелей метро»V1,V2,V3: ρH2H(V1,V2)=ρH2H(V1,V3)=ρH2H(V2,V3)=3;

Кубические окрестности.
Определение. Множество всех единичных n-кубов вместе со всеми своими гранями в Rсn, имеющих общую вершину (целую точку), - кубическая n-окрестность этой точки.
Число n-кубов в кубической n-окрестности (ортантов) равно 2n.
Общее число кубических граней всех размерностей в n-окрестности равно 5n, что следует из общего принципа кодирования кубических граней. Единичные отрезки (как декартовы сомножители) кодируются двумя буквами 2 и -2 (в положительном и отрицательном направлениях) по каждому измерению, а трансляции тремя буквами -1,0,1; т.е. общий алфавит-пятиричный (-2,-1,0,1,2).

Общая комбинаторная схема кодирования кубических граней.
Для n-куба:
(одна буква для обозначения наличия единичного отрезка в декартовом произведении по данному измерению) + (две буквы для обозначения наличия или отсутствия трансляции по данному измерению)?
ΣF(n,k)=(1+2)n; F(n,k)=C(n,k) 2n-k; число k-граней в n-кубе
Для кубической n-окрестности радиуса 1:
(две буквы для отрезков в положительном и отрицателном направлениях)+(три буквы для трансляций в положительном и отрицательном направлениях и отсутствия трансляции)
ΣF(n,k)=(2+3)n; F(n,k)=C(n,k)2k 3n-k;число k-граней в n-окр.

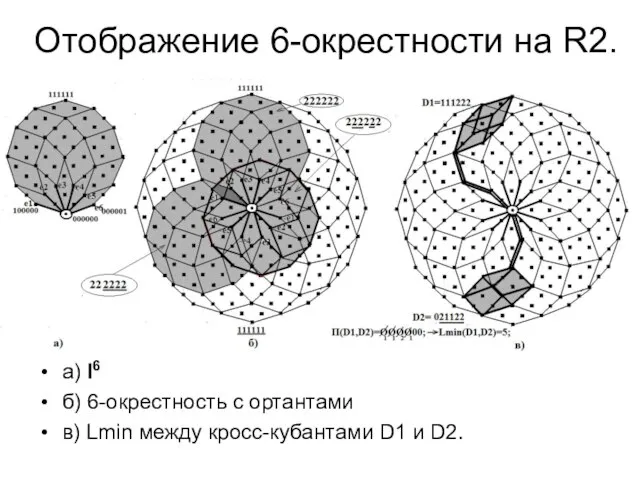
Отображение 6-окрестности на R2.
a) I6
б) 6-окрестность с ортантами
в) Lmin между кросс-кубантами D1 и D2.

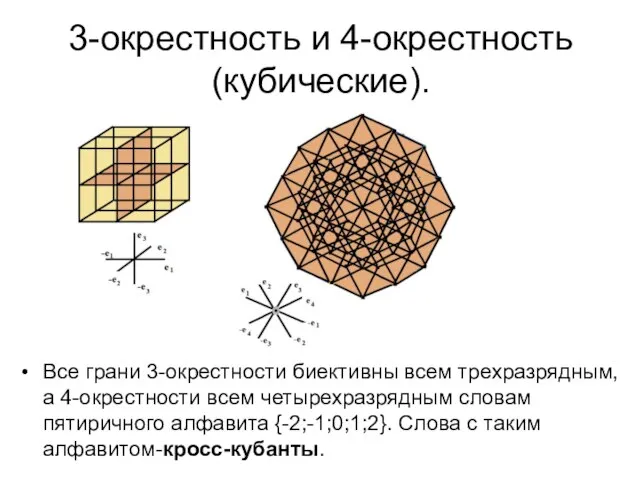
3-окрестность и 4-окрестность (кубические).
Все грани 3-окрестности биективны всем трехразрядным, а 4-окрестности всем четырехразрядным словам пятиричного алфавита {-2;-1;0;1;2}. Слова с таким алфавитом-кросс-кубанты.

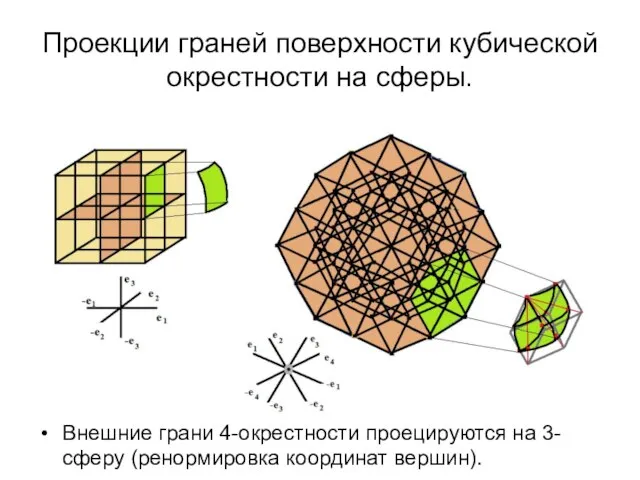
Проекции граней поверхности кубической окрестности на сферы.
Внешние грани 4-окрестности проецируются на 3-сферу (ренормировка координат вершин).

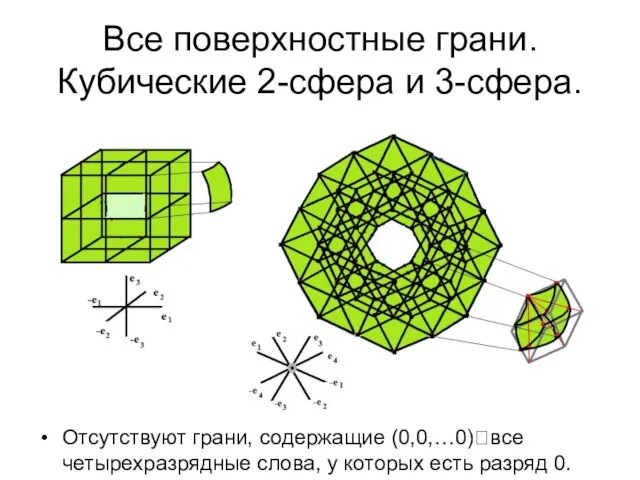
Все поверхностные грани. Кубические 2-сфера и 3-сфера.
Отсутствуют грани, содержащие (0,0,…0)?все четырехразрядные слова, у которых есть разряд 0.

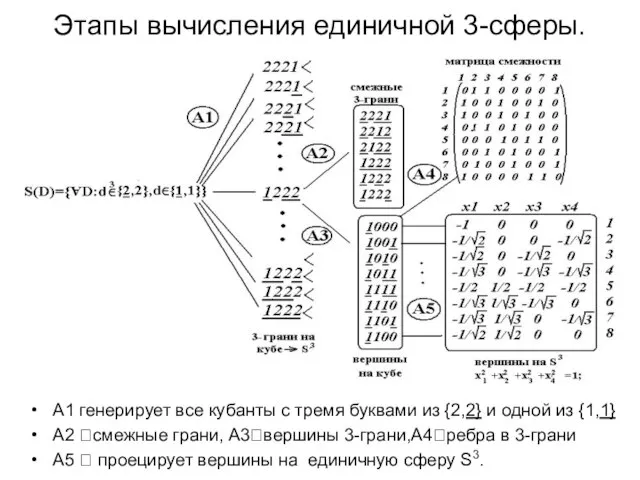
Этапы вычисления единичной 3-сферы.
A1 генерирует все кубанты с тремя буквами из {2,2} и одной из {1,1}
А2 ?смежные грани, А3?вершины 3-грани,А4?ребра в 3-грани
А5 ? проецирует вершины на единичную сферу S3.

Вычислимость и энумератор.
А1-энумерация всех кубических 3-граней для проекции на сферу с помощью матрицы (столбцы соотв.знакам):
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1101 1110 1111
2221 2221
2212 2212
2122
1222 1222
Порядок генерации по строкам с 1-ой по 4-ую, т.о. №(2212)= (m-1)16+5=21, где m-номер разряда с 1, 5-номер столбца.
№=63?63/16=3(15)?3+1(строка 4),15 (столбец1110)=1222

Экстраполяция на n-мерный случай.
Кубическая n-мерная сфера как множество n-мерных кубических граней:
Sn(D)={∀ D(n+1):dn∈{2,2},d∈{1,1}};
Общее правило проекции на сферу (А5):
(x1,x2,…xn)?(ξ1,ξ2,…ξn);
ξi=xi/√Σxk2;
(x)-вершина (целая точка) на кубической грани, (ξ)-вершина на сфере
Алгоритмы А1,А2,А3,А4 без изменения.

Сравнительная анатомия 4-окрестности и единичной S3.
Вершин 81; 80;
Ребер 216; 208;
2-Граней 216; 192;
3-Граней 96; 64;
4-Граней 16; 0;

Матрица смежности для вершин на S3 (проекции вершин кубической 4-окрестности) 80х80
Обозначения координат: 1?+;0?0; 1?⎪; элементов в матрице: 1?х; 0?.;(++0- ?1101)

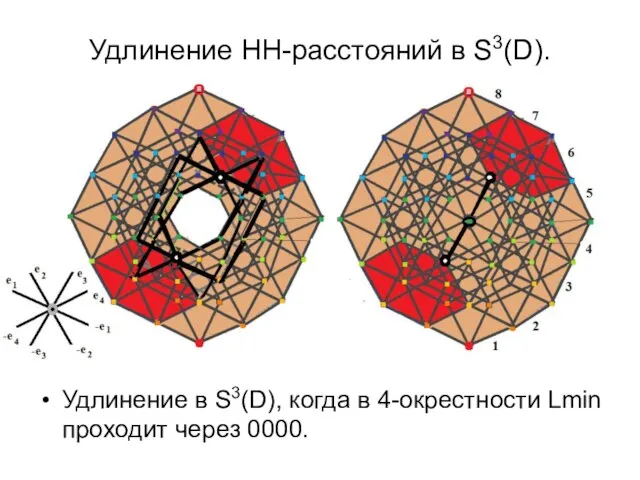
Удлинение НН-расстояний в S3(D).
Удлинение в S3(D), когда в 4-окрестности Lmin проходит через 0000.

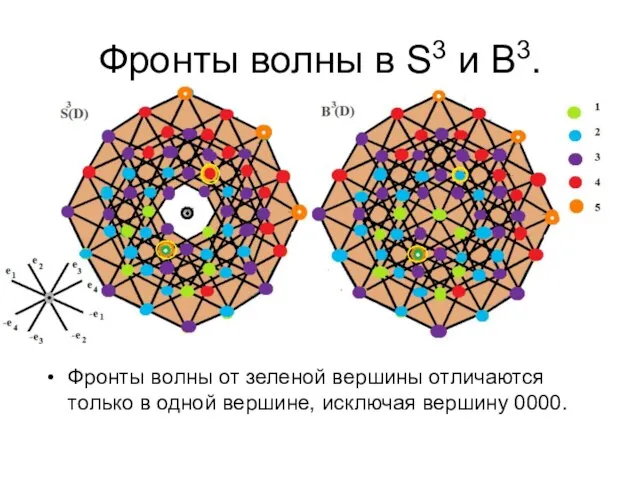
Фронты волны в S3 и B3.
Фронты волны от зеленой вершины отличаются только в одной вершине, исключая вершину 0000.

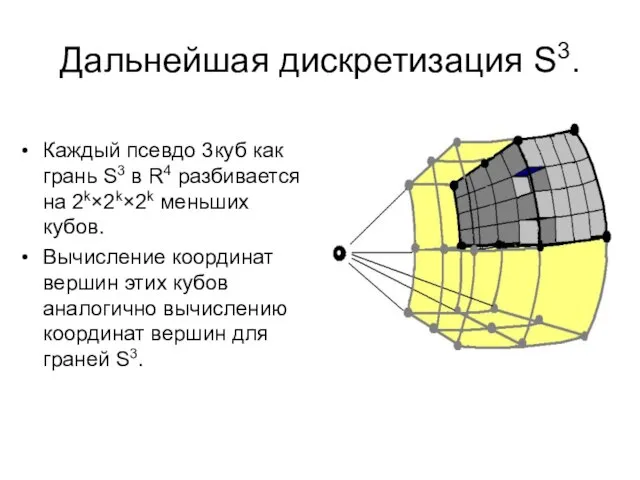
Дальнейшая дискретизация S3.
Каждый псевдо 3куб как грань S3 в R4 разбивается на 2k×2k×2k меньших кубов.
Вычисление координат вершин этих кубов аналогично вычислению координат вершин для граней S3.

Дальнейшие вычисления при дискретизации S3.
Пример разбиения единичной S3 на 64х64=4096 псевдокубических граней.(Продолжение «Этапы вычисления 3-сферы»)

Графическое приближение S3
4-окрестность без внутренних граней, содержащих (0000)
Проекция вершин на сферу Σ xi2=1; i=1-4;

Дискретизация, триангуляция и мозаичное разбиение 3-сферы по аналогии с 2-сферой.
Оценки для суперкомпьютера.
Сравнительные данные с MITgcm.
Дискретизация 16,32,64 для S2? 256х6;1024x6;4096x6.(псевдоквадратов).
Дискретизация 16,32,64 для S3? 4Kx64=1/4K2;32Kx64=2K2;256Kx64=16K2; K2~106
Одноразовый проход по всему многообразию S3 с числом операций106 для каждого дискрета возможен на «Чебышеве» за секунды.

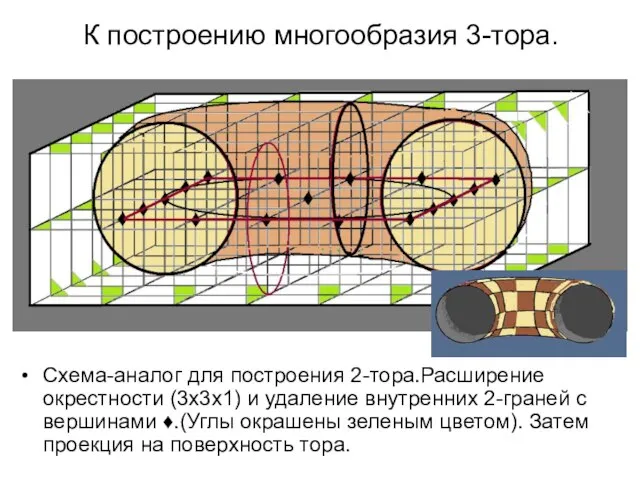
К построению многообразия 3-тора.
Схема-аналог для построения 2-тора.Расширение окрестности (3х3х1) и удаление внутренних 2-граней с вершинами ♦.(Углы окрашены зеленым цветом). Затем проекция на поверхность тора.

О значении визуализации.
If I can’t picture it, I can’t understand it. А.Эйнштейн

Графическое обеспечение многомерных кубических структур.
Адекватное представление – алгебраическое, геометрическое- скорее метафорическое. Наиболее эффективно построение графического образа прямо по алгебраической форме.
2d и 3d отображения многомерных структур должны комментироваться описанием искажений (афинных и др.) в графике.
Особое значение приобретает цвет, как средство выделения подмножеств с определенными свойствами.
Динамика осмотра и анимация эволюции- важный элемент для графики многомерных объектов.
Создание специального ПО целесообразно как надстройка над открытыми системами Open GL и VRML.

Проблема масштабирования.
Визуализация многомерных структур должна предусматривать элементы масштабирования, прежде всего по размерности пространств n. Для кубических структур настройку параметров изображения (вершин,ребер и т.д.) для комфортной визуализации.
Поскольку технические возможности аппаратуры весьма ограничены, специальное ПО должно позволять не только сигнализировать о практической невозможности отображения целиком объекта, но и предлагать воспроизвести допустимый фрагмент объекта.

Qcubant 1.0
Программная среда для визуализации и рассчётов над кубантами.

Встроенный интерпретатор
В Qcubant встроен интерпретатор языка javascript, позволяющий быстро, без компиляции, в режиме реального времени производить операции над ними и выводить результат в соотвествии с заданным режимом отображения.
Также поддерживается ряд операций над кубантами и кубическими комплексами – это операции “умножение кубантов”, “выпуклая оболочка”, “наибольший общий кубант”, и другие
Добавлена поддержка кросскубантов как подкласс кубантов со смещением по осевым направлениям.

Возможности визуализации
2 варианта визуализации – трехмерный и двумерный.
Настраивамые параметры отображения – цвет, форма граней и вершин
Настравивамый репер (базис) для отображения
Возможность вывода в VRML
Возможность создания множественных отображений, соотвествующих одной сцене

Применение на суперкомпьютерах
Структура приложения организована так, что часть программы, которая отвечает за логику отделена, и может использоваться самостоятельно. Эту часть можно использовать на суперкомпьютерах для рассчетов, связанных с кубантами.
С другой стороны, эта часть используется в приложении Qcubant и можеn быть вынесена оттуда как отдельная программная библиотека.

Возможности системы
Отрисовка кубантов
Простейшие операции
Отображение в виде двух проекций – 2D и 3D
Встроенный интерпретатор языка Javascript

Вид программы
Внешний вид программы- слева,
Снизу javascript-представление,
Вверху двумерная проекция для кубантов 5-мерного куба.

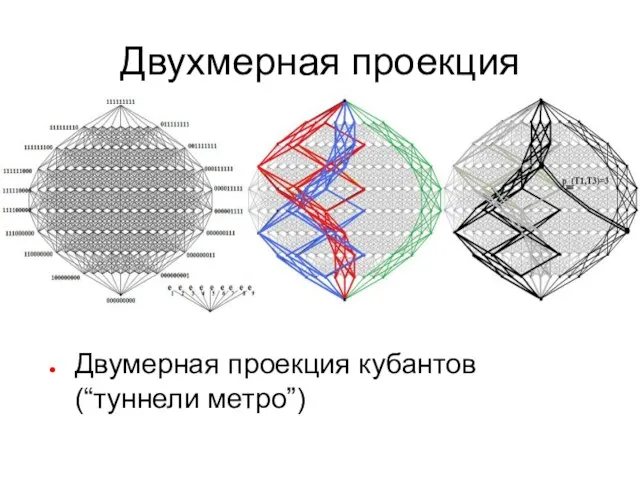
Двухмерная проекция
Двумерная проекция кубантов (“туннели метро”)

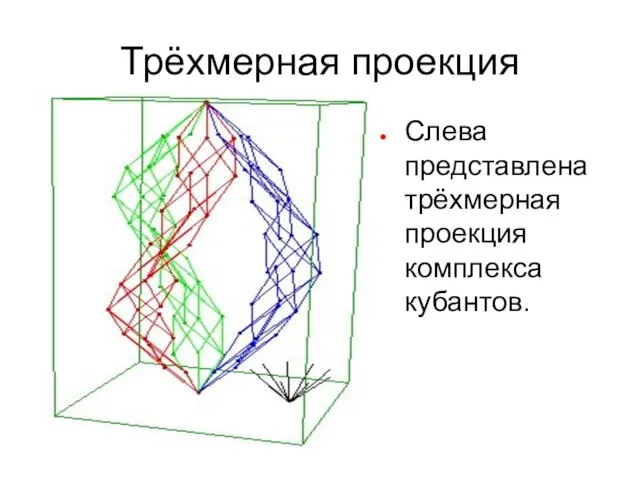
Трёхмерная проекция
Слева представлена трёхмерная проекция комплекса кубантов.

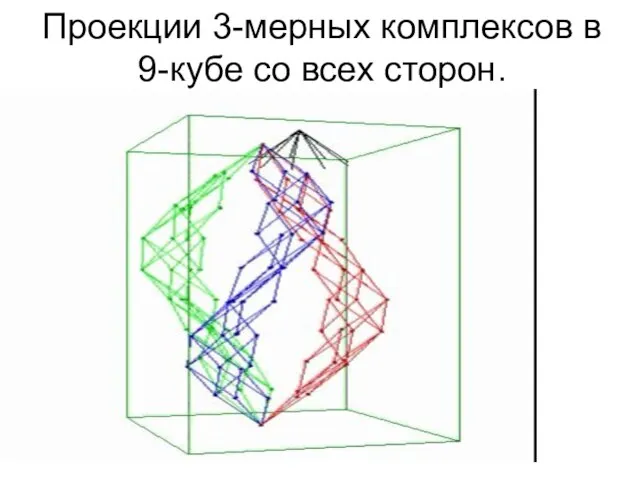
Проекции 3-мерных комплексов в 9-кубе со всех сторон.

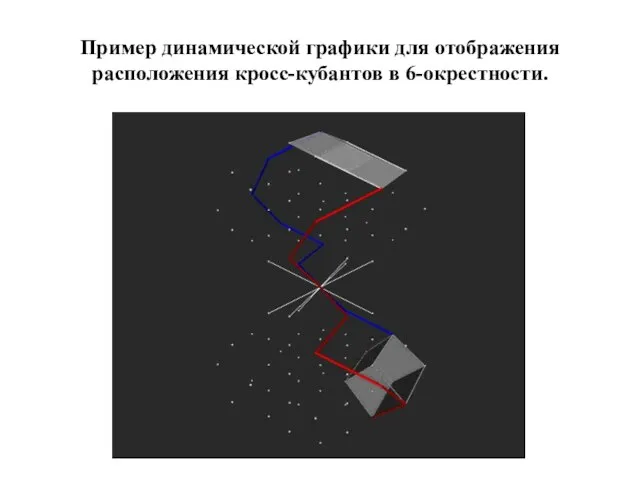
Пример динамической графики для отображения расположения кросс-кубантов в 6-окрестности.

Эмуляция операторов и расчеты с их использованием на суперкомпьютере «Чебышев»
Пользовательская нотация используется для хранения кросс-кубантов в файлах и графического отображения.
Машинная нотация используется непосредственно в вычислениях.

Нотации для представления кросс-кубантов (пользовательская, машинная).
Пользовательская нотация используется для хранения кросс-кубантов в файлах и графического отображения.
Машинная нотация используется непосредственно в вычислениях.

Пользовательская нотация
{[,,]()( )[ ]( )( )…[ ]( )}…{ }
{ } - комплекс из единичных n-кубов
[ x1,x2,…,xn ] – координаты единичного n-куба в составе комплекса { }
( c1,c2,…,cn ) – кросс-кубант, в составе единичного n-куба. Разряды кросс-кубанта могут быть из пользовательского алфавита {Ø1,0,1,2, Ø2,-1,-2}. Кросс-кубанты, входящие в состав единичного n-куба, следуют сразу за координатами этого куба: [ ]( )( )…
В дальнейшем, по мере усложнения задач, нотация может быть расширена. Например, могут быть добавлены идентификаторы комплексов: {A }{B } и т.д.

Машинная нотация
Разряды кросс-кубанта могут быть из машинного алфавита {0,1,2,3, 4,6,7}. Машинная нотация получается из пользовательской путем следующего преобразования :
Ø1 ->0, 0->1,1->2, 2->3, Ø2 ->4, -1->6, -2->7
Реализованы две функции для перехода от одной нотации к другой и обратно.

Основные структуры данных и формат файлов для представления кросс-кубантов.
Формат файла {A[,,]()( )[ ]( )( )…[ ]( )}…{B }… Нотация соответствует пользовательской.
Структуры данных представляют собой набор классов:
- класс “Куб”, содержащий координаты единичного n-куба и набор кросс-кубантов в составе этого куба. Под координатами куба понимаются координаты его начальной точки (точка с координатами (0,0,..,0) в локальной системе координат данного куба). Набор кросс-кубантов реализован в виде одномерного массива.
- класс ”Комплекс”. Содержит идентификатор комплекса и все единичные n-кубы, входящие в состав данного комплекса. Кубы хранятся в виде одномерного массива.
Если необходимо работать с несколькими комплексами, то они, в свою очередь, помещаются в массив.
Все массивы динамические и реализованы средствами библиотеки STL C++. Размерность пространства, в данной реализации, одинакова для всех объектов.

Вспомогательные структуры данных.
Используется ряд вспомогательных структур, которые ускоряют процесс вычисления. В частности, таблицы для операции умножения кросс-кубантов, хаусдорфова сжатия, операции выделения выпуклой оболочки, кодированного представления кросс-кубантов, таблица для разложения кросс-кубантов на составляющие (и полуцелые) точки.

Структуры данных, используемые в параллельной реализации.
В параллельной реализации используются аналогичные основные и вспомогательные структуры данных. Также присутствуют специфические дополнительные структуры - буферы для обмена информацией между вычислительными узлами.
Добавлена возможность представления кросс-кубанта как самостоятельного элемента, а не в составе единичного n-куба. Это вызвано необходимостью обмена данными между вычислительными узлами, который требует линейного размещения данных в памяти, в не структурированном виде. В таком представлении кросс-кубант задается следующим образом: [идентификатор комплекса][координаты единичного n-куба][кросс-кубант]. В памяти машины он представляется как одномерный массив.

Набор последовательных функций для работы с кросс-кубантами.
- Вспомогательные функции , функции для работы с файлами и подготовки к вычислениям. Функции для генерации комплексов из кросс-кубантов (алгоритм произвольной кривой, замкнутые комплексы), функции для чтения \ записи данных из текстовых файлов, функции для анализа содержимого файлов (парсер) и заполнения структур данных в памяти компьютера, функция перевода из пользовательского представления кубантов в машинное и обратно.
Реализованы некоторые геометрические операции с n-мерными векторами.
- Операторы для работы с кросс-кубантами: умножения, хаусдорфова сжатия, проверки на пересечение и определения кратчайшего пути, выделения выпуклой оболочки, выделения границы.
- Функции для работы с комплексами кросс-кубантов внутри единичного n-куба: функция умножения двух комплексов, функция проверки на пересечение, функция сжатия, функция проверки на связность комплекса и выяснения его топологической структуры, функция определения кратчайшего пути между комплексами, функция определения Хаусдорф-Евклидова и Хаусдорф- Хеммингова расстояния между комплексами, функция рекурсивного построения гамильтонова цикла в единичном n-кубe, выделение границы.
- Функции на уровне комплексов из n-кубов: вычисление Хаусдорф-Евклидова расстояния.

Набор параллельных функций для работы с кросс-кубантами.
- Функция для “по-кубантного” представления комплексов (см. выше Структуры данных) и функция распределения входных данных по вычислительным узлам. Размещение данных происходит равномерно по всем узлам, с точностью до кросс-кубанта. Для разных алгоритмов применяются различные схемы распределения, в зависимости от характера задачи (степени информационной зависимости).
- Функция вычисления Хаусдорф-Евклидова расстояния между комплексами в n-мерном пространстве и функции определения Хаусдорф-Евклидова и Хаусдорф- Хеммингова расстояния между комплексами внутри единичного n-куба.

Графическое представление.
Графическое отображение средствами VRML. Трехмерное сферическое представление n-мерных комплексов кросс-кубантов внутри единичного n-куба (n-окрестность).

Тестовые задачи с использованием функций инструментария.
- Тестирование и отладка всех реализованных на данный момент функций инструментария.
- Комплексная задача вычисления Хаусдорф-Хеммингова расстояния между двумя n-комплексами внутри единичного n-куба. Задача вычисления Хаусдорф-Евклидова расстояния между двумя n-комплексами в n-мерном пространстве. Сравнение с результатами оператора метрической волны в трехмерном случае.
Комплексная задача определения Хаусдорф-Хеммингова расстояния для всех пар кросс кубантов внутри единичного n-куба.
Задачи решались как на однопроцессорном компьютере, так и на кластере.

Особенности параллельной реализации задачи определения Хаусдорф-Евклидова расстояния между двумя n-комплексами в n-пространстве.
Довольно сильная информационная зависимость задачи, так как комплексы распределены по всем вычислительным узлам.
Решение задачи, в первую очередь, ориентировано на саму возможность расчета Хаусдорф-Евклидова расстояния для больших n за счет использования памяти кластера.
Алгоритм распределения “по-кубантный”.
В трехмерном случае результаты вычислений данным алгоритмом и алгоритмом метрической волны совпали.

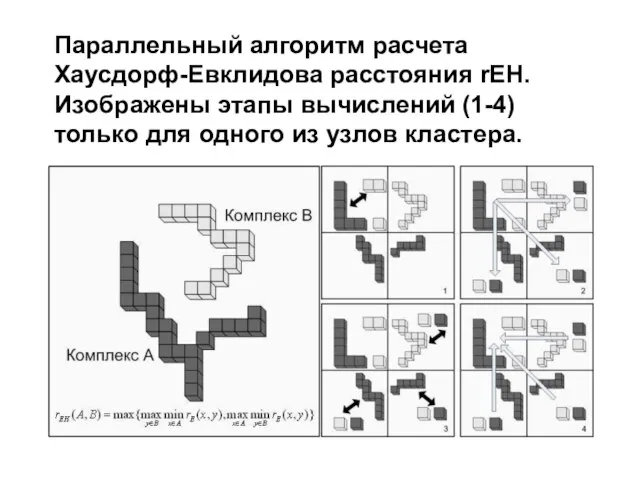
Параллельный алгоритм расчета Хаусдорф-Евклидова расстояния rEH. Изображены этапы вычислений (1-4) только для одного из узлов кластера.

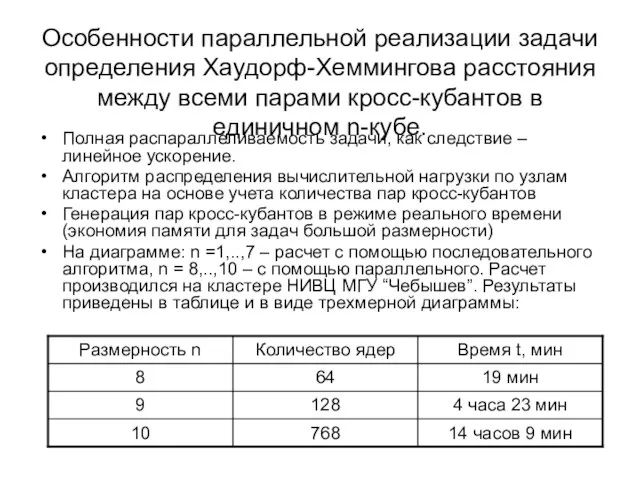
Особенности параллельной реализации задачи определения Хаудорф-Хеммингова расстояния между всеми парами кросс-кубантов в единичном n-кубе.
Полная распараллеливаемость задачи, как следствие – линейное ускорение.
Алгоритм распределения вычислительной нагрузки по узлам кластера на основе учета количества пар кросс-кубантов
Генерация пар кросс-кубантов в режиме реального времени (экономия памяти для задач большой размерности)
На диаграмме: n =1,..,7 – расчет с помощью последовательного алгоритма, n = 8,..,10 – с помощью параллельного. Расчет производился на кластере НИВЦ МГУ “Чебышев”. Результаты приведены в таблице и в виде трехмерной диаграммы:

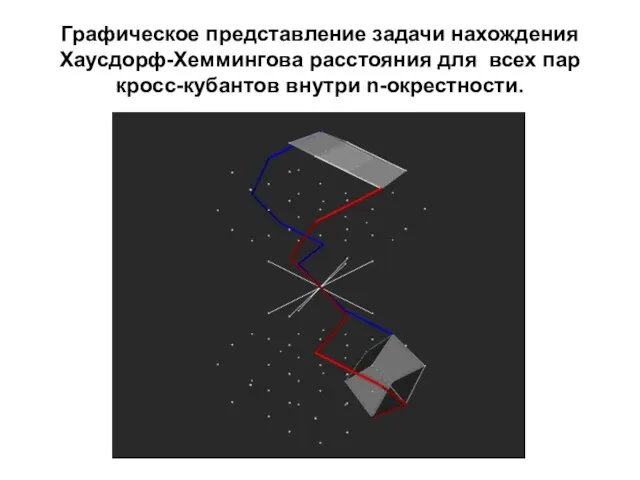
Графическое представление задачи нахождения Хаусдорф-Хеммингова расстояния для всех пар кросс-кубантов внутри n-окрестности.

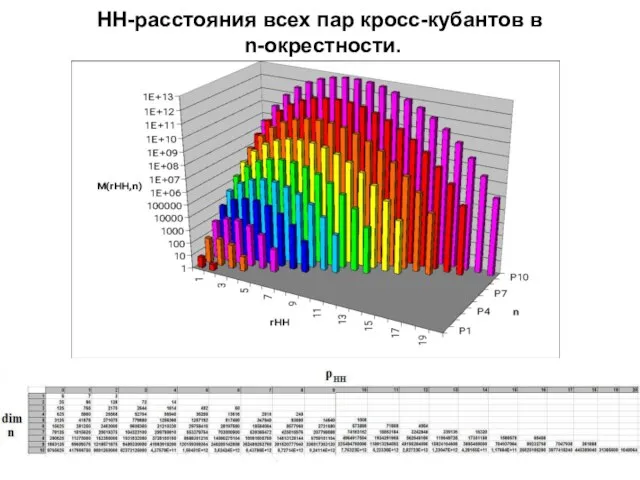
НН-расстояния всех пар кросс-кубантов в
n-окрестности.

Перспективы развития (теоретические).
Развитие алгебры кубантов для n-окрестности радиуса r>1. Модификация (универсализация) алфавита.
Развитие методов проецирования кубических комплексов и многообразий на гладкие тела.
Стыковка с предикатными конструкциями пространственной логики.
Развитие стринговой структуры организации памяти компьютера и символьных операций.

Перспективы технические.
Разработка архитектуры сопроцессора, ориентированного на решение многомерных комбинаторно-топологических задач.
Моделирование сопроцессора на уровне межрегистровых пересылок.
Оценки экономичности аппаратных и программных реализаций операций сопроцессора и его места в суперкомпьютерной структуре.

Литература
1.Новиков С.П. Топология. Москва-Ижевск.РХД.2002.
2.Долбилин Н.П.,Штанько М.А.,Штогрин М.И. Кубические многообразия в решетках.// Изв.РАН.Сер. матем.1994.58. вып.2.93-107
3.Деза М.,Штогрин М. Вложение графов в гиперкубы и кубические решетки.// Успехи матем. наук.1997.52.№6.155-156.
4.Деза М.,Штогрин М. Мозаики и их изометрические вложения.// Изв. РАН.Сер. матем.2002.66.№3.3-22.
5.Matveev S., Polyak M. Finite type Invariants of Cubic Complexes.//Act.Appl.Math.75.2003.pp.125-132.
6.Бухштабер В.М., Панов Т.Е. Торические действия в топологии и комбинаторике. МЦНМО.2004.
7.Бухштабер В.М. Кольцо простых многогранников и дифференциальные уравнения.// Труды МИРАН.2008.263.18-43.
8.Kontchakov R., Pratt-Hartmann J.,Wolter F., Zakharyaschev. Spatial Logics with Connectedness Predicates.//Log.Methods in Comp.Science. Vol.6(3:5) 2010,pp.1-43.
9.Marshall J., Adcroft A., Campin J-M., Hill C. Atmosphere-Ocean modelling exploiting fluid isomorphisms.//Boston.MIT.2002
10.Hamming R.W. Error detecting and error correcting codes.// Bell system Tech.Journal. 1950.29(2) 147-160
11.Baez J., Stay M. Phisics, topology, logics and computation: a Rosetta Stone//arXiv:0903.0340v3[quant-ph].6 June 2009
12.Baez J.,Lauda A. A Prehistory of n-categorical Physics.// arXiv: 0908.2469.v1 [hep-th] 18 Aug 2009.