Слайд 3Записать формулу n-го члена
арифметической прогрессии

Слайд 7Записать формулу n-го члена
геометрической прогрессии

Слайд 10Записать формулы суммы n членов арифметической прогрессии

Слайд 13Записать формулы суммы n членов геометрической прогрессии

Слайд 17a3 = a2 +d
d = a2 – a1
d = 2 – 6
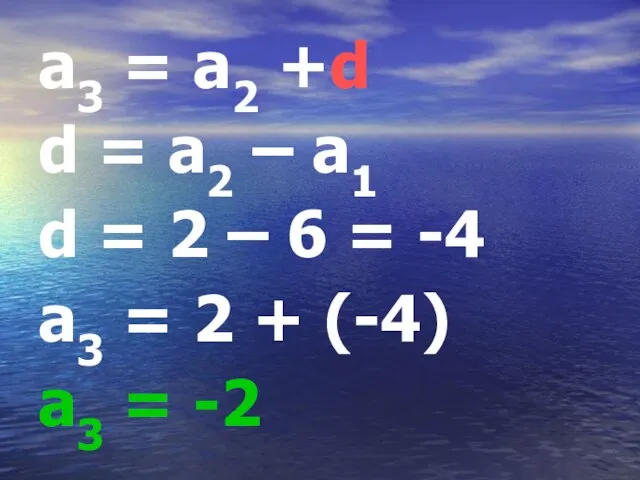
= -4
a3 = 2 + (-4)
a3 = -2
Слайд 18a10 = a1 + 9d
a10 = 1+ 9 * 4
a10 = 37
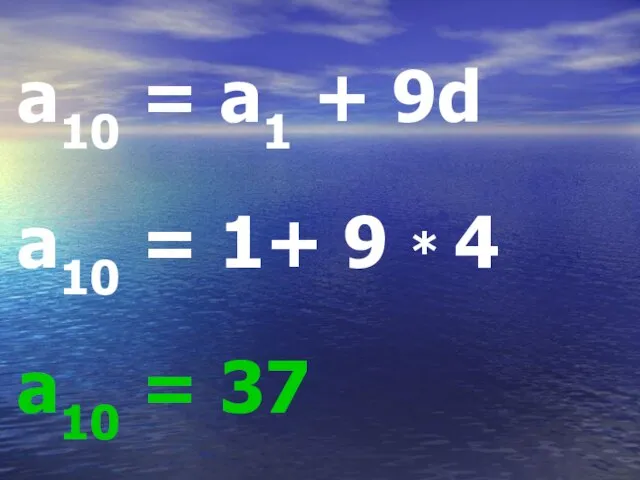
Слайд 20q = bn+1 : bn
q = b2 : b1
q = 4:8
q =
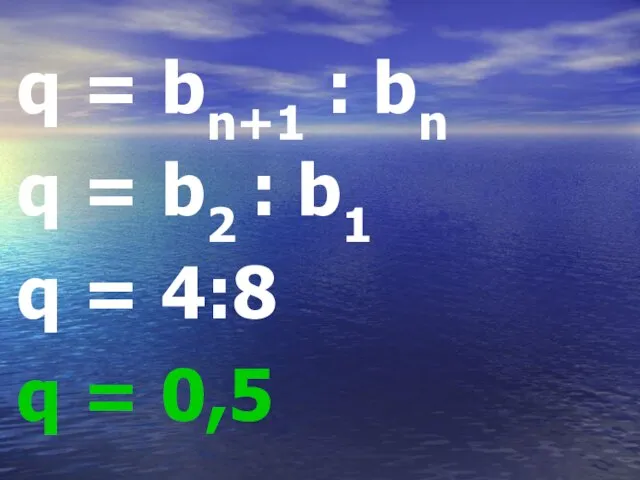
0,5
Слайд 21b3 = b2 * q
q = b2 : b1
q = 3 :
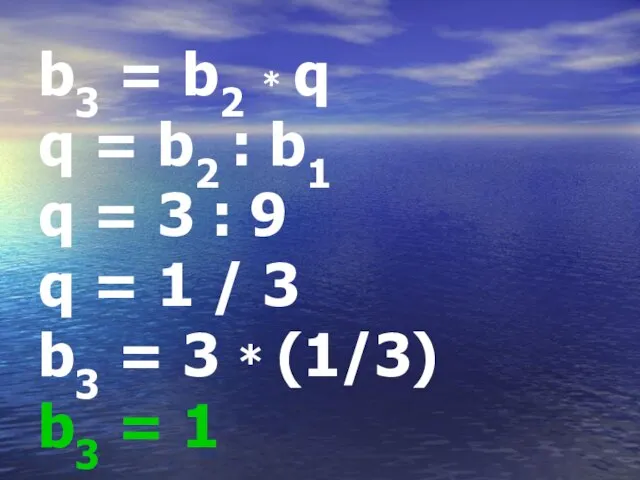
9
q = 1 / 3
b3 = 3 * (1/3)
b3 = 1
Слайд 22S = a1 + an n
2
S = 2a1 + (n-1)d n
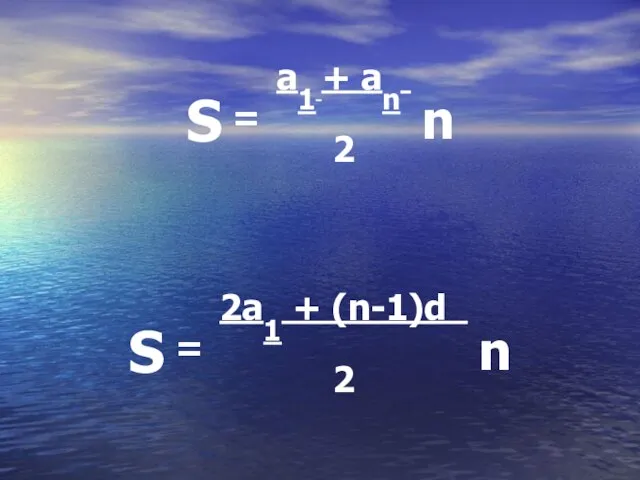
2
Слайд 23S = a1 + a5 * 5
2
S = 6 + (-6)

* 5
2
S = 0
Слайд 24S = 2a1 + 4d 2
S = 2*(-20)+4*10 2
S = 0

Слайд 25S = b1 (qn-1) q - 1
S = bnq – b1 1
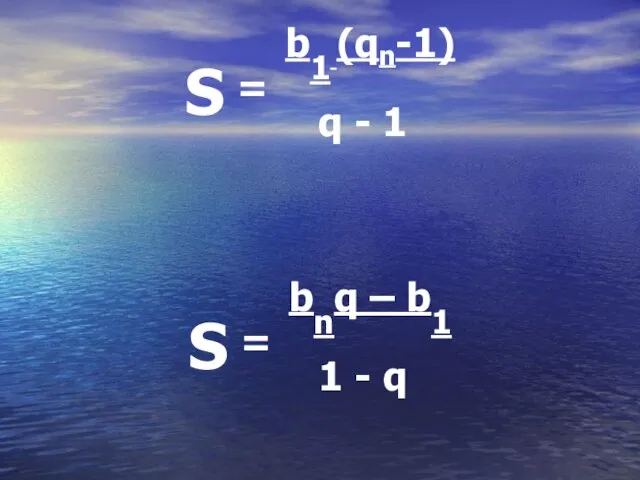
- q
Слайд 27 В геометрической прогрессии (bn) известно, что b5 · b11 = 8.
Чему

равно b8?
Слайд 28Между числами 1 и 81 вставьте три таких числа, чтобы они вместе

с данными числами образовали геометрическую прогрессию
Слайд 29В равносторонний треугольник, сторона которого равна 16 см, вписан другой треугольник, вершинами

которого являются середины сторон первого. Во второй треугольник таким же способом вписан третий и т.д. Найдите периметр восьмого треугольника.
Слайд 30bn = b1 · q n-1
b8 = b1 · q7
b8 = 16
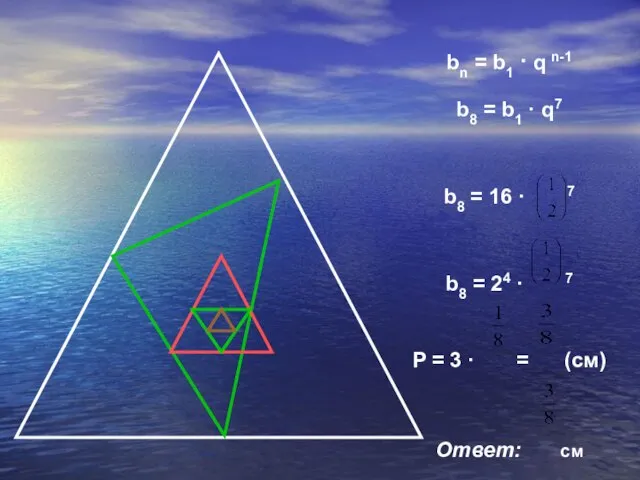
· 7
b8 = 24 · 7
P = 3 · = (cм)
Ответ: cм
Слайд 31
P1 = 3·16 =48(см)
P8 = P1· 7
P8 = 48· 7
P8 =
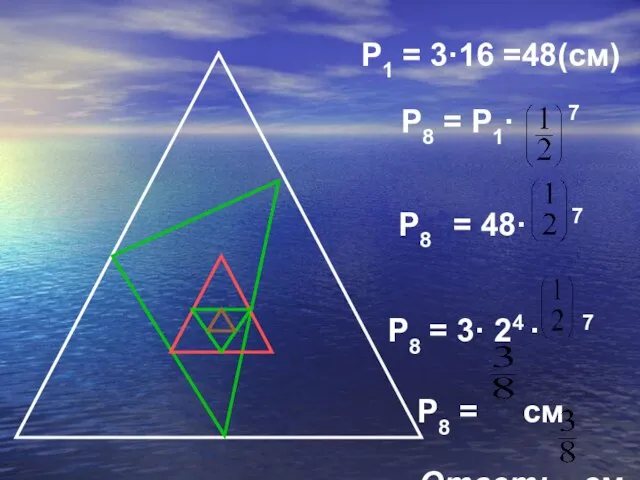
3· 24 · 7
P8 = см
Ответ: см
Слайд 32Домашнее задание
Сборник стр.113 №163,
стр.101 №65;
Учебник стр.164 «Проверь себя!»

Слайд 33Три числа, сумма которых равна 31, можно рассматривать как три последовательных члена

геометрической прогрессии или как первый, второй, седьмой члены арифметической прогрессии. Найдите эти числа.


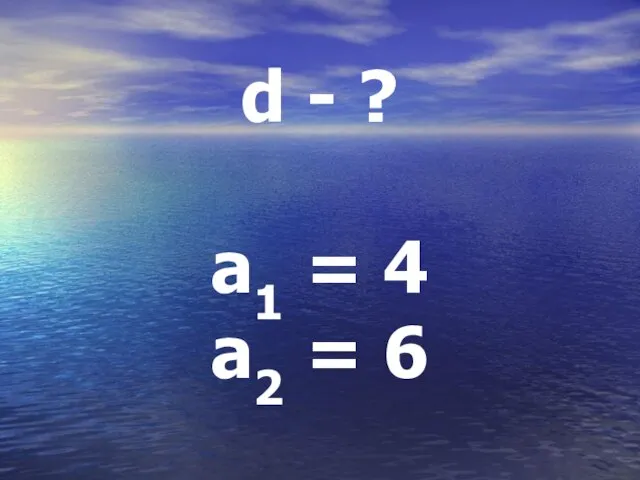
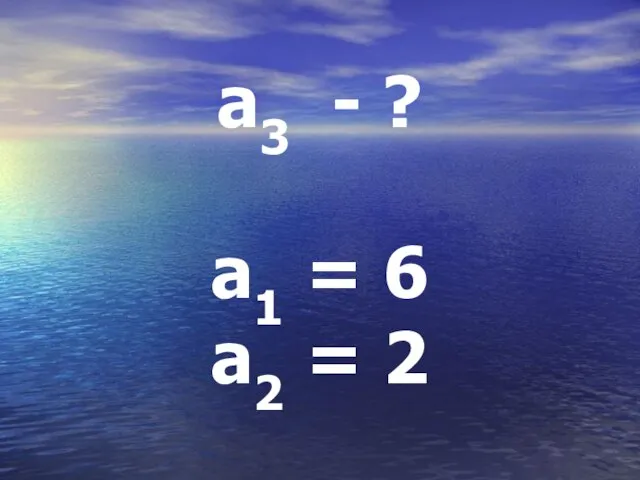
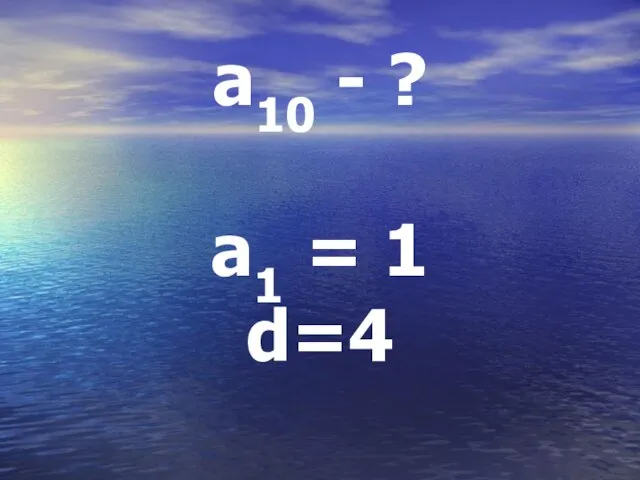

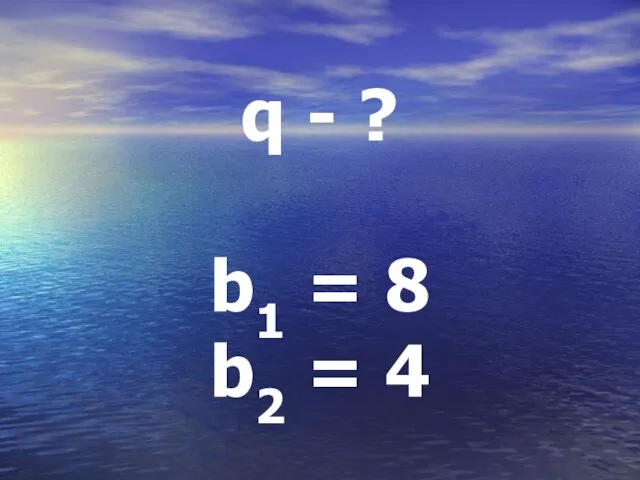
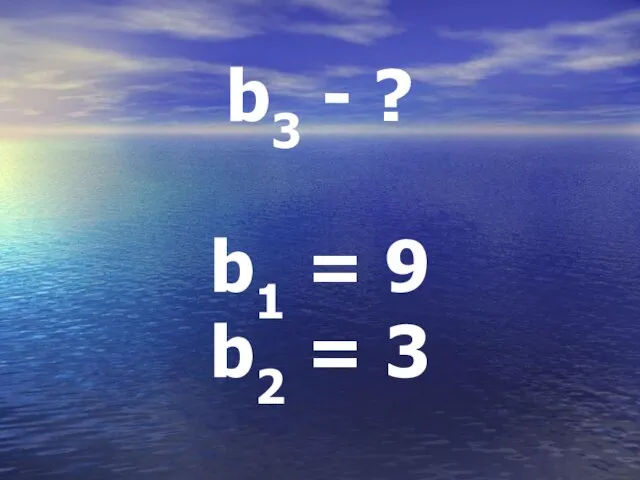

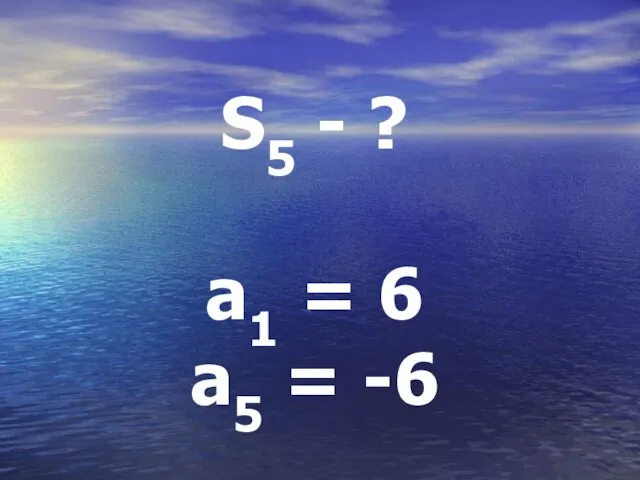
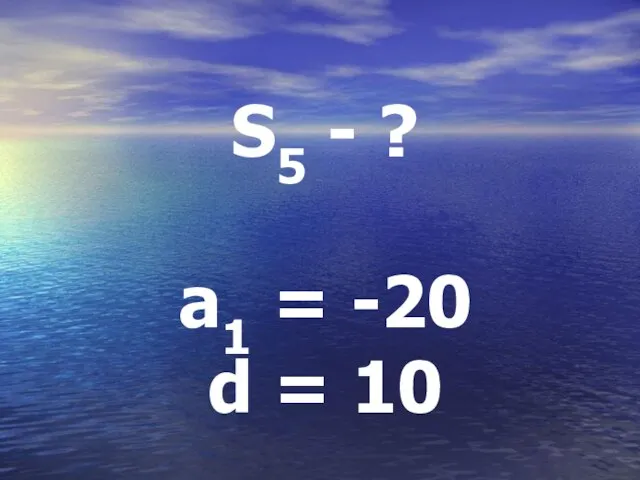

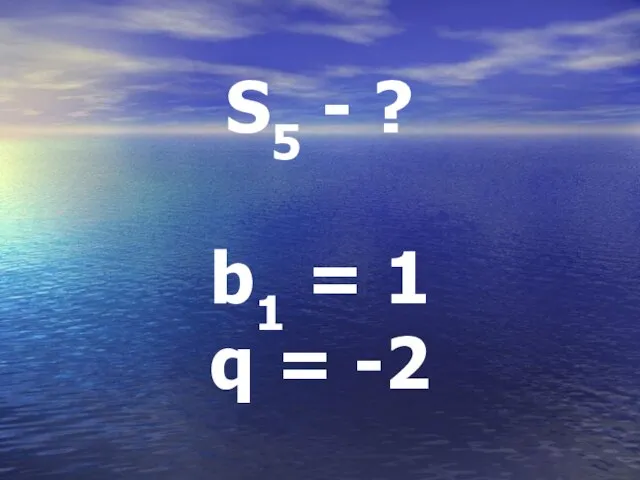
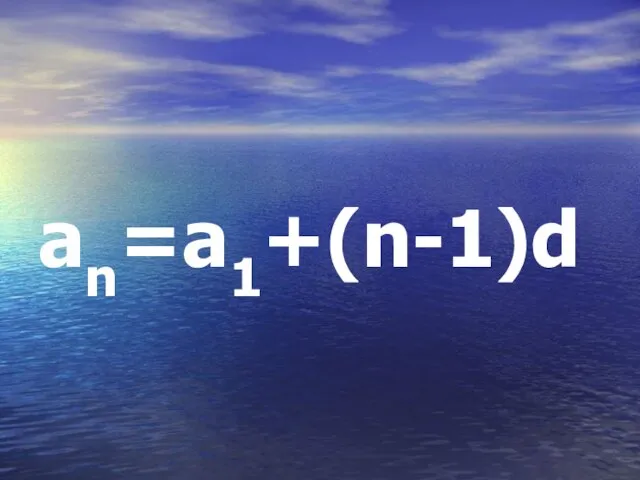
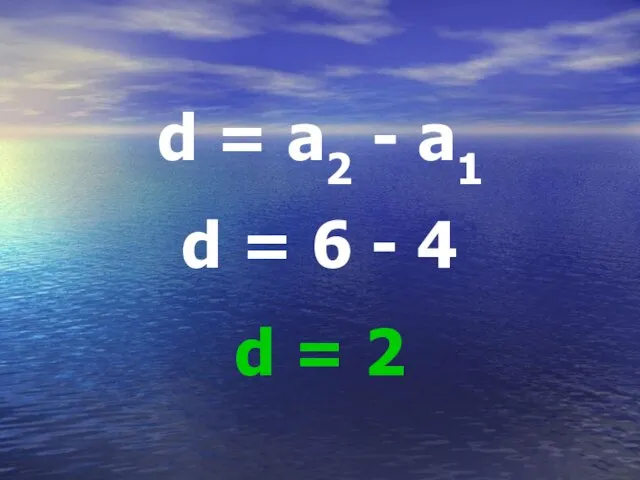
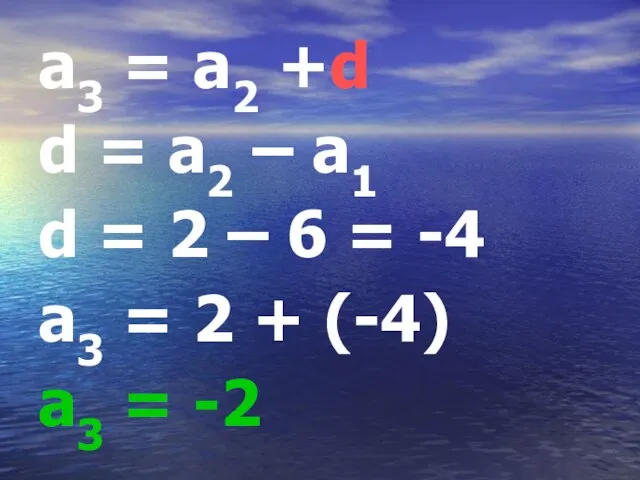
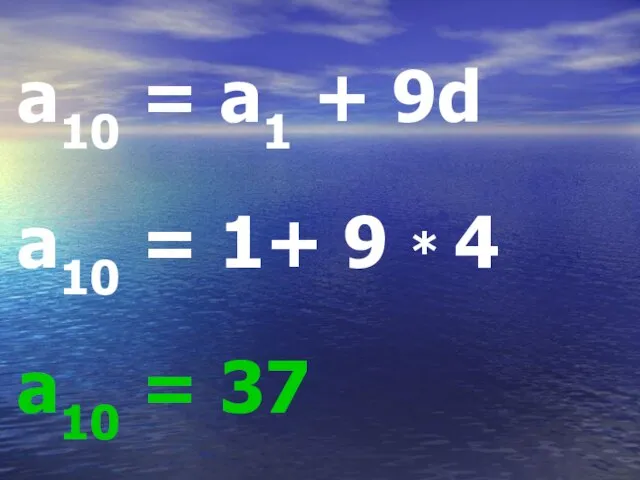
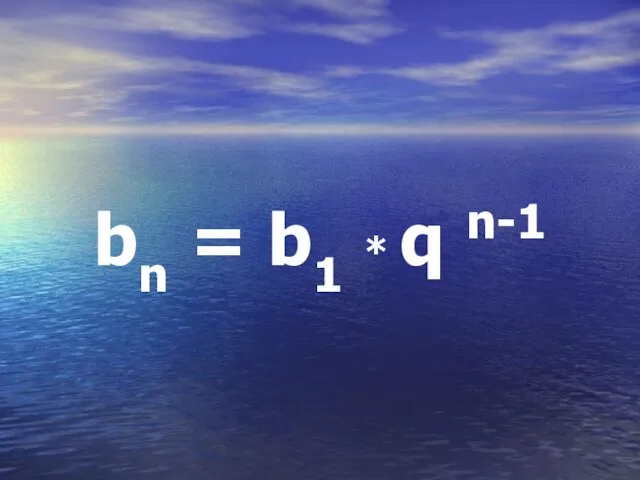
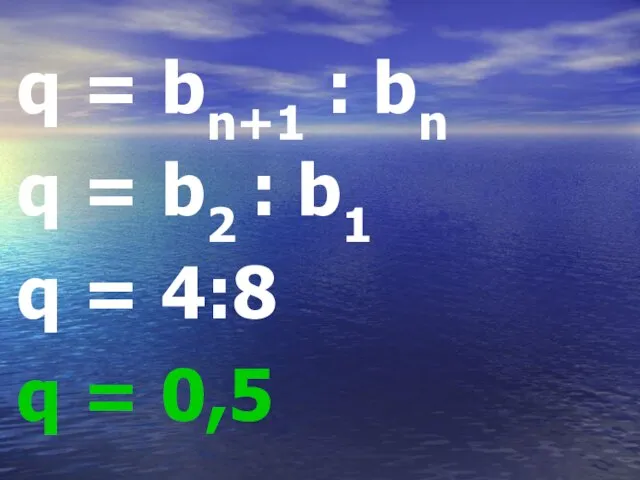
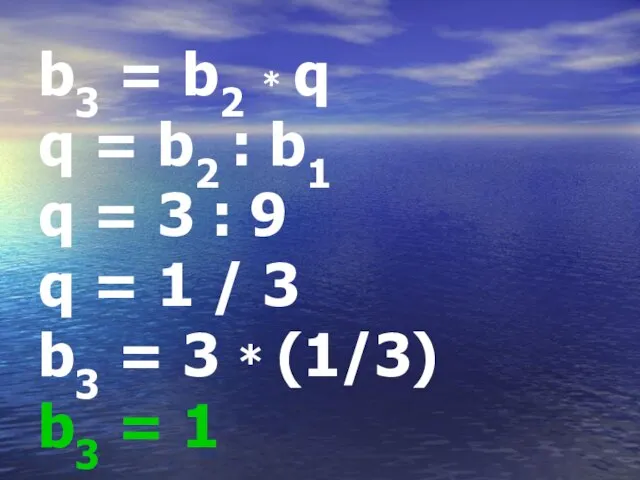
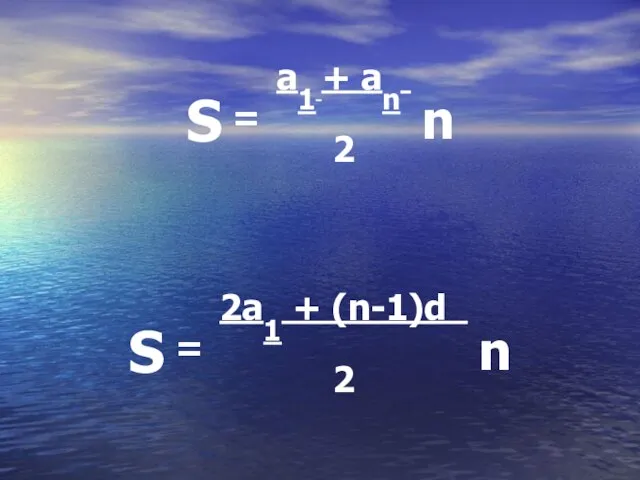


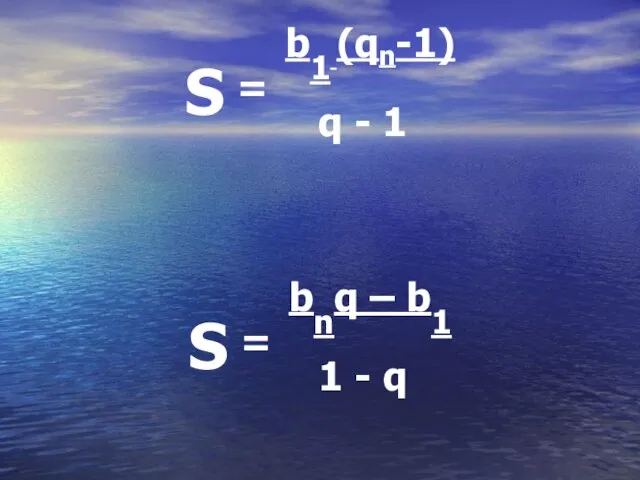








 Размножение на клеточном и организменном уровне
Размножение на клеточном и организменном уровне Ионная полимеризация
Ионная полимеризация Кадры Общая численность сотрудников ЦКП – 29 человек Среди них: 2 главных научных сотрудника, 2 ведущих научных сотрудника, 3 старших
Кадры Общая численность сотрудников ЦКП – 29 человек Среди них: 2 главных научных сотрудника, 2 ведущих научных сотрудника, 3 старших Презентация на тему Наш город в творчестве художников
Презентация на тему Наш город в творчестве художников  Проект: Cross-Border Road Traffic SafetyБезопасность трансграничного дорожного движения
Проект: Cross-Border Road Traffic SafetyБезопасность трансграничного дорожного движения Ароматерапия для здоровья человека
Ароматерапия для здоровья человека О мерах по совершенствованию деятельности территориальных органов федеральных органов исполнительной власти
О мерах по совершенствованию деятельности территориальных органов федеральных органов исполнительной власти Проблема и позиция автора
Проблема и позиция автора Возвращаясь домой в большом городе
Возвращаясь домой в большом городе Банки Китая
Банки Китая Презентация на тему Музыка раннего барокко (1600—1654)
Презентация на тему Музыка раннего барокко (1600—1654)  Отдел покрытосеменные растения
Отдел покрытосеменные растения Хоккейная викторина
Хоккейная викторина СЛАВЬСЯ, ОТЕЧЕСТВО!
СЛАВЬСЯ, ОТЕЧЕСТВО! Общие положения ЭК строевая подготовка
Общие положения ЭК строевая подготовка Продукция пантового оленеводства и функциональные средства для здоровья
Продукция пантового оленеводства и функциональные средства для здоровья Презентация на тему Олигосахариды ПОЛИСАХАРИДЫ.
Презентация на тему Олигосахариды ПОЛИСАХАРИДЫ.  Подготовка к ЕГЭ Задание А12
Подготовка к ЕГЭ Задание А12 Виды случайных событий
Виды случайных событий Презентация на тему Вид: критерии и структура
Презентация на тему Вид: критерии и структура  Логистические схемы маркетплейсов
Логистические схемы маркетплейсов Стандарты ГОСТ 34
Стандарты ГОСТ 34 Услуги ООО Машаудит
Услуги ООО Машаудит Транспорт в моем городе
Транспорт в моем городе Античный атомизм обоснование материализма
Античный атомизм обоснование материализма Семьи для подростков группы риска.
Семьи для подростков группы риска. Әжетқана сызбасы (жуалы)
Әжетқана сызбасы (жуалы) Пословицы и поговорки о труде
Пословицы и поговорки о труде