Содержание
- 2. Тема 1.4. Логические основы ЭВМ, элементы и узлы Занятие 10. Базовые логические операции и схемы. Таблицы
- 3. Англичанин Джордж Буль (1815-1864, математик-самоучка), на фундаменте, заложенном Лейбницем, создал новую область науки - Математическую логику
- 4. Алгебра логики (высказываний) работает с высказываниями. Различают: Логические константы (логические утверждения) – конкретные частные утверждения (И/Л)
- 5. 3. Логические функции ( логические формулы) – сложные логические выражения, образованные из простых и связанных логическими
- 6. Логические операции Отрицание (инверсия). Обозначение: НЕ А, ¬А, А={Дети любят игрушки} = {Дети НЕ любят игрушки}
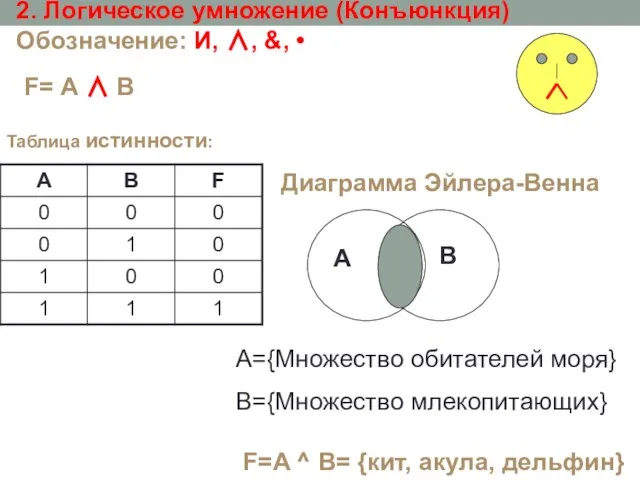
- 7. 2. Логическое умножение (Конъюнкция) Обозначение: И, ∧, &, • F=A ^ B= {кит, акула, дельфин} Таблица
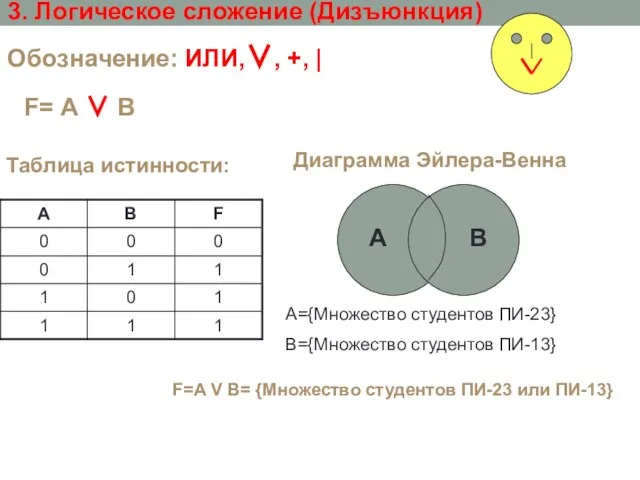
- 8. 3. Логическое сложение (Дизъюнкция) Обозначение: ИЛИ,∨, +, | F=A V B= {Множество студентов ПИ-23 или ПИ-13}
- 9. 4. ИМПЛИКАЦИЯ (логическое следование) условие следствие ЕСЛИ, ... ТО ... => условие следствие Если будет дождь,
- 10. 4. ИМПЛИКАЦИЯ (логическое следование) Обозначение: А→В, А⇒В Например, один философ испытал сильнейшее потрясение, узнав от Бертрана
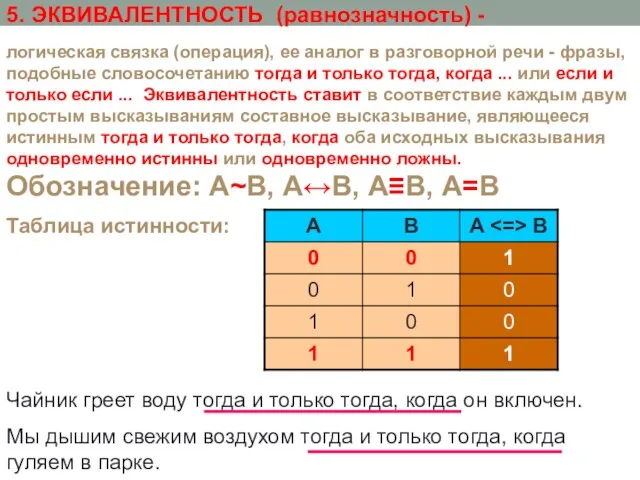
- 11. 5. ЭКВИВАЛЕНТНОСТЬ (равнозначность) - Чайник греет воду тогда и только тогда, когда он включен. Мы дышим
- 12. РЕШИМ ЗАДАЧИ: Определите, в каком порядке необходимо вычислять значение логического выражения: 1) ¬ А & ¬
- 13. Вычисление логических выражений Пример1. Вычислить значение логического выражения «(2·2=5 или 2·2=4}) и (2·2 ≠ 5 или
- 14. Задание 2. Определите истинность составного высказывания состоящего из простых высказываний: А={Принтер – устройство вывода информации} В={Процессор
- 15. ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ ПО ЛОГИЧЕСКОМУ ВЫРАЖЕНИЮ Таблицу, показывающую, какие значения принимает сложное высказывание при всех сочетаниях
- 16. Порядок действий: Количество строк в таблице Q=2n, где n - количество переменных (аргументов), здесь n =
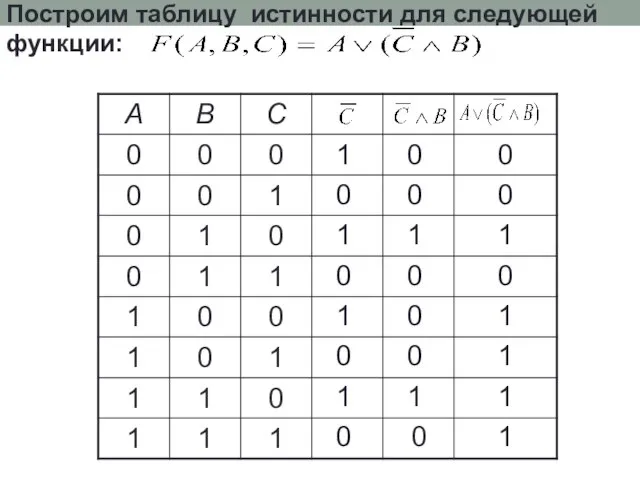
- 17. Построим таблицу истинности для следующей функции: 1 1 1 1 0 0 0 0 0 0
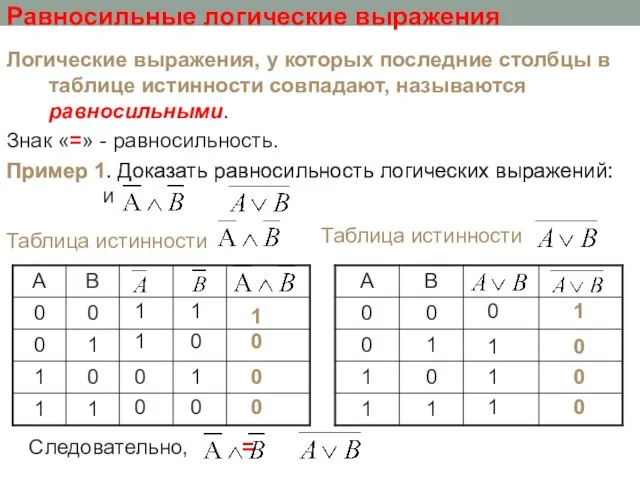
- 18. Пример 1. Доказать равносильность логических выражений: и Равносильные логические выражения Логические выражения, у которых последние столбцы
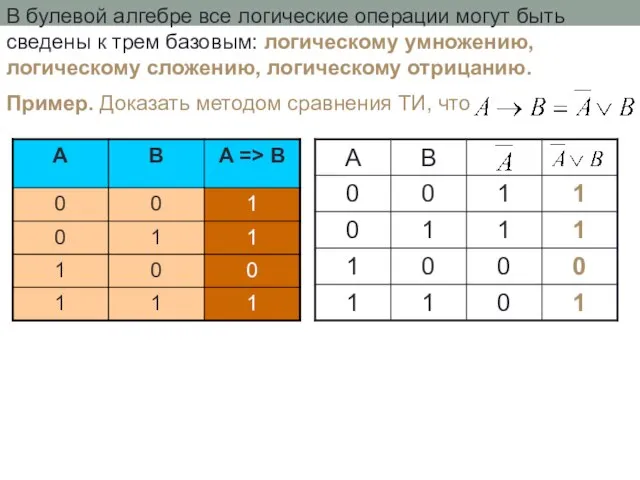
- 19. В булевой алгебре все логические операции могут быть сведены к трем базовым: логическому умножению, логическому сложению,
- 20. Пример. Доказать, пользуясь ТИ, что операция эквивалентности равносильна выражению 1 0 1 0 1 0 1
- 21. Законы алгебры логики и свойства логических операций используются для упрощения логических выражений (минимизации логических функций)
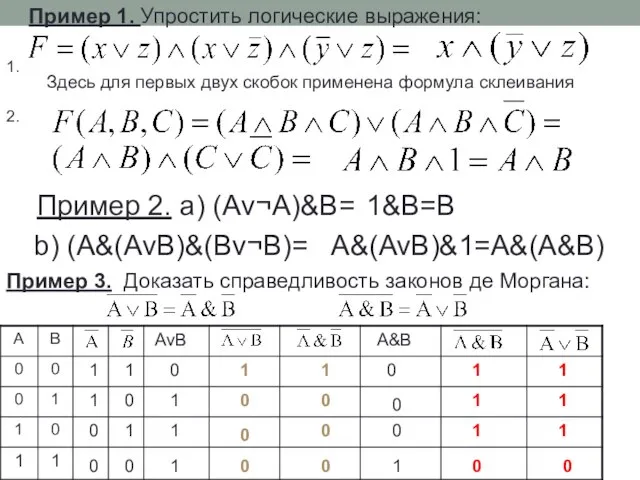
- 23. Пример 1. Упростить логические выражения: Здесь для первых двух скобок применена формула склеивания 1. 2. Пример
- 24. Вопросы для размышления: Ученый, заложивший основы математической логики? Ученый, создавший новую область науки – математическую логику?
- 25. Решение логических задач Способы решения: Табличный. Графический (Графы). Средствами алгебры логики. Дополнительный материал
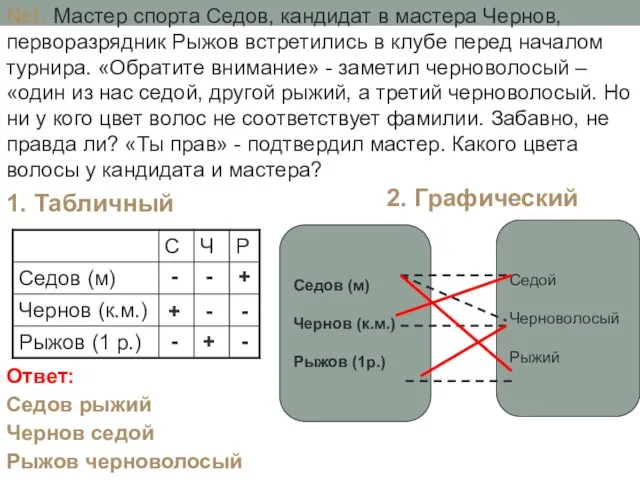
- 26. №1. Мастер спорта Седов, кандидат в мастера Чернов, перворазрядник Рыжов встретились в клубе перед началом турнира.
- 27. Алгоритм: Изучить условие задачи. Выделить простые условия и обозначить их буквами. Записать условия на языке алгебры
- 28. 3. Средствами алгебры логики Выделим простые условия: А=«Седов черноволосый» В=«Седов рыжий» С=«Чернов седой» D=«Чернов рыжий» Е=«Рыжов
- 29. №2. В каждой из двух аудиторий может находиться либо каб. Информатики, либо каб. Экономики. Таблички: на
- 30. №3. В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и
- 31. №4. Три школьника, Миша (М), Коля (К) и Сергей (С), остававшиеся в классе на перемене, были
- 33. Скачать презентацию






















 Chereduyuschiesya_glasnye_v_korne_slova
Chereduyuschiesya_glasnye_v_korne_slova Эмоционально-смысловой метод И.Ю. Шехтера
Эмоционально-смысловой метод И.Ю. Шехтера Презентация на тему Уникумы природных комплексов России
Презентация на тему Уникумы природных комплексов России  Сессия Госконтроль 2.0: образ будущего
Сессия Госконтроль 2.0: образ будущего Произведение искусства в эпоху его технической воспроизводимости
Произведение искусства в эпоху его технической воспроизводимости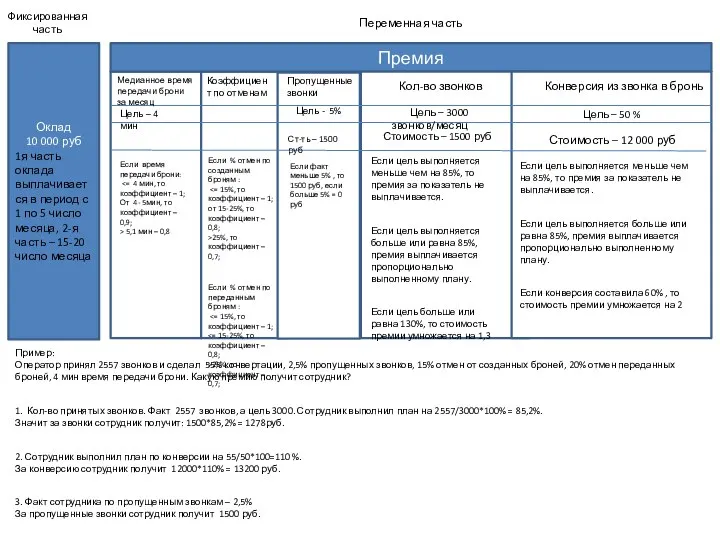 Финансовая мотивация
Финансовая мотивация Выделяя основные элементы общества, их взаимосвязь и взаимодействие, учёные характеризуют общество как
Выделяя основные элементы общества, их взаимосвязь и взаимодействие, учёные характеризуют общество как Картошечка по-деревенски
Картошечка по-деревенски Поздравление с днем рождения внучке
Поздравление с днем рождения внучке Иголка-белошвейка
Иголка-белошвейка Начертательная геометрия и инженерная графика. Тесты
Начертательная геометрия и инженерная графика. Тесты Формирование инфокоммуникационной инфраструктуры Казанского университетского образовательного округа
Формирование инфокоммуникационной инфраструктуры Казанского университетского образовательного округа Социологический факультет МГУ им.Ломоносова
Социологический факультет МГУ им.Ломоносова Добросовестность в ГП
Добросовестность в ГП Метод кейсов
Метод кейсов  Концепция круглогодичного профессионального Индор гольф центра
Концепция круглогодичного профессионального Индор гольф центра Презентация на тему Звёздное небо 1 класс
Презентация на тему Звёздное небо 1 класс Теория организации направления современного развития
Теория организации направления современного развития Что такое ФГТ?
Что такое ФГТ? Fotoreport
Fotoreport Историческая разминка Подготовила: студентка 1 курса группы 1404 Лухманова Ирина
Историческая разминка Подготовила: студентка 1 курса группы 1404 Лухманова Ирина Эволюция темы «маленького человека» в русской литературе
Эволюция темы «маленького человека» в русской литературе Презентация на тему Первый закон термодинамики
Презентация на тему Первый закон термодинамики Методы определения показателей обилия насекомых в луговых /лесных экосистемах
Методы определения показателей обилия насекомых в луговых /лесных экосистемах Презентация на тему Внутреннее строение и размножение рыб
Презентация на тему Внутреннее строение и размножение рыб Презентация на тему Электрическое сопротивление проводника. Удельное сопротивление
Презентация на тему Электрическое сопротивление проводника. Удельное сопротивление Логика, стиль и язык закона
Логика, стиль и язык закона luxe collection. Коллекция препаратов для ухода за кожей лица
luxe collection. Коллекция препаратов для ухода за кожей лица