Содержание
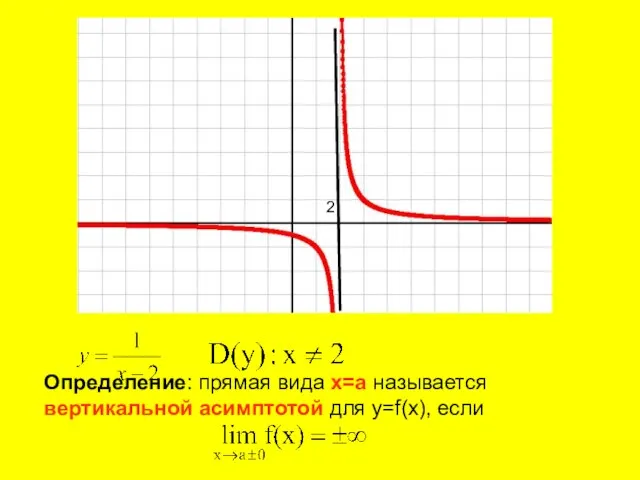
- 2. 2 Определение: прямая вида x=a называется вертикальной асимптотой для y=f(x), если
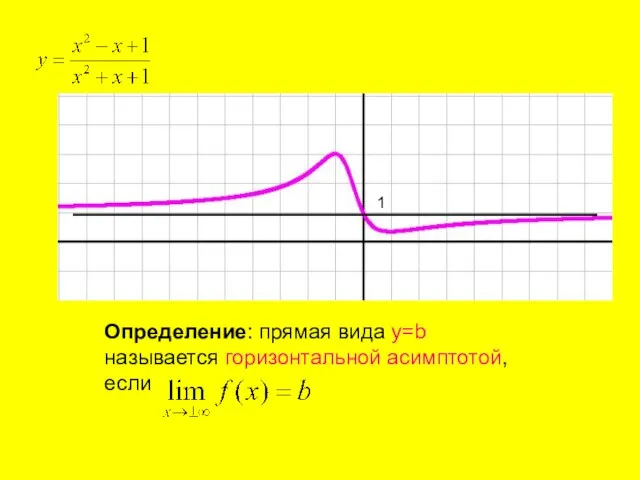
- 3. 1 Определение: прямая вида y=b называется горизонтальной асимптотой, если
- 4. 2
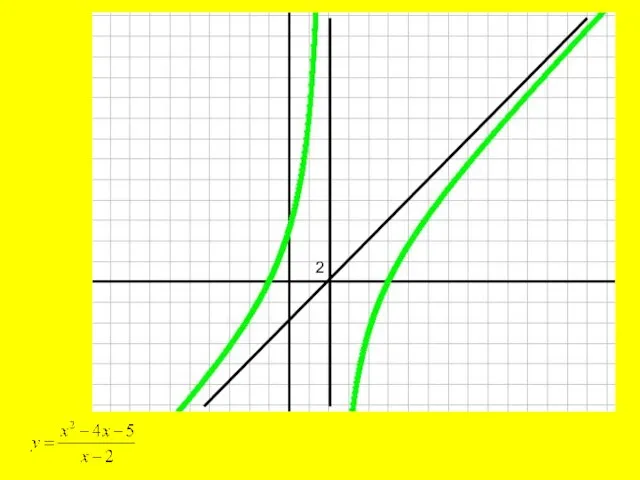
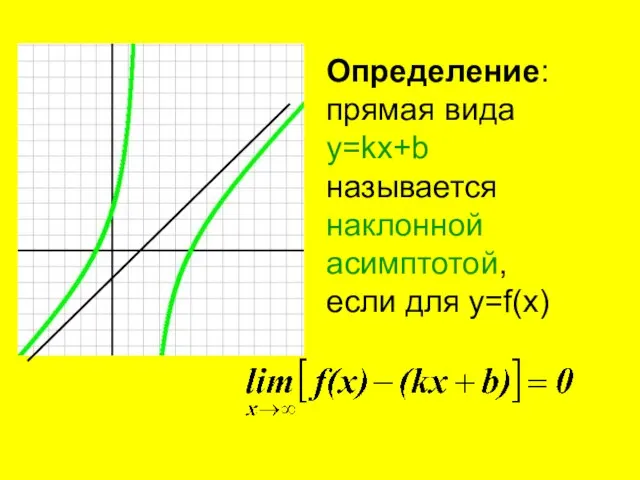
- 5. Определение: прямая вида y=kx+b называется наклонной асимптотой, если для y=f(x)
- 6. Примечания: 1. Вертикальные асимптоты существуют в точках разрыва функции. 2. У дробно-рациональной функции горизонтальные асимптоты существуют,
- 7. Области существования графика на координатной плоскости. -4 -2 2 + - + - -4 -2 2
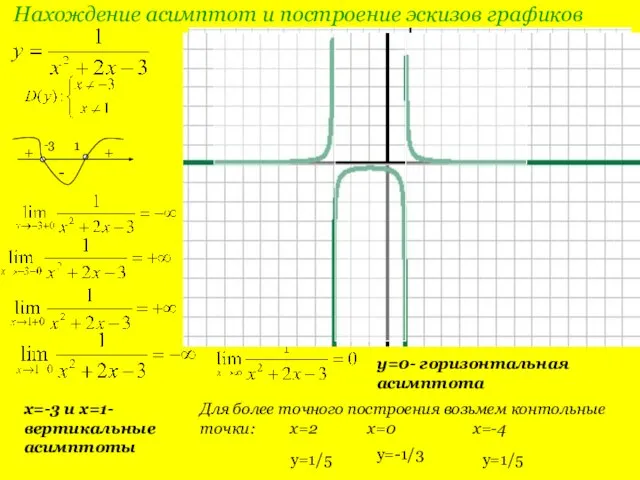
- 8. Нахождение асимптот и построение эскизов графиков -3 1 + - + 1 -3 x=-3 и x=1-вертикальные
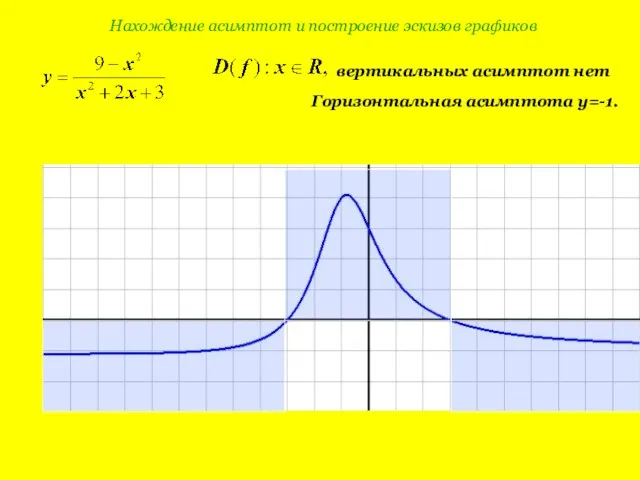
- 9. Нахождение асимптот и построение эскизов графиков вертикальных асимптот нет Горизонтальная асимптота y=-1.
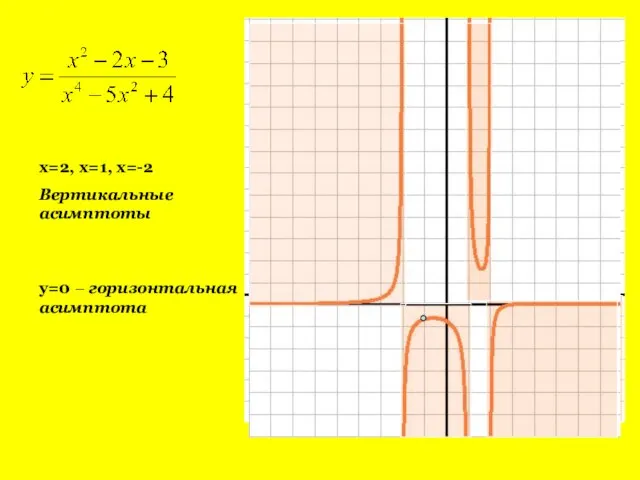
- 10. x=2, x=1, x=-2 Вертикальные асимптоты y=0 – горизонтальная асимптота
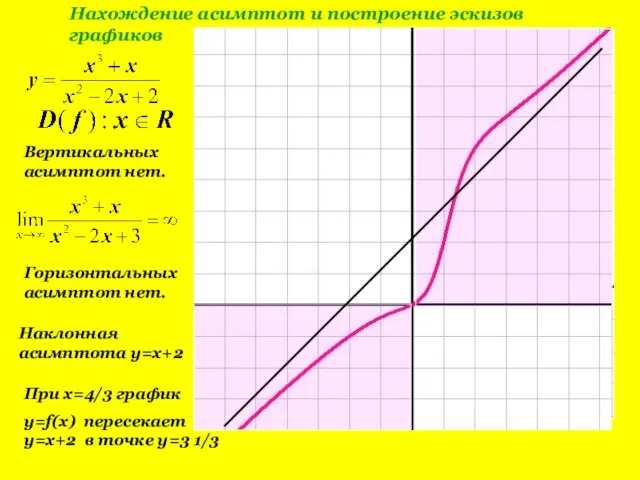
- 11. Вертикальных асимптот нет. Горизонтальных асимптот нет. Наклонная асимптота y=x+2 При x=4/3 график y=f(x) пересекает y=x+2 в
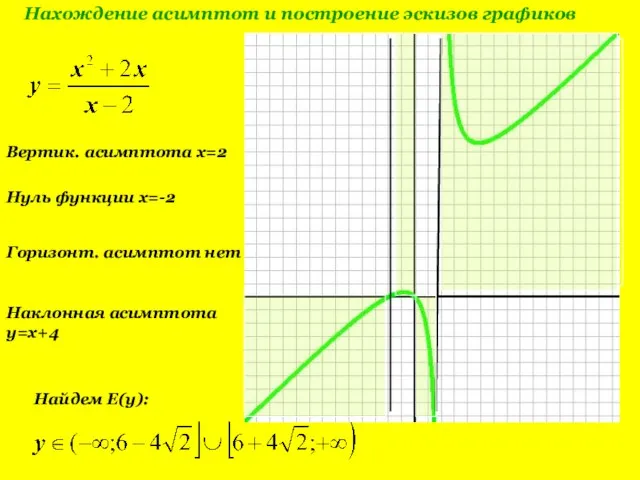
- 12. Нахождение асимптот и построение эскизов графиков Вертик. асимптота x=2 2 Горизонт. асимптот нет -2 Нуль функции
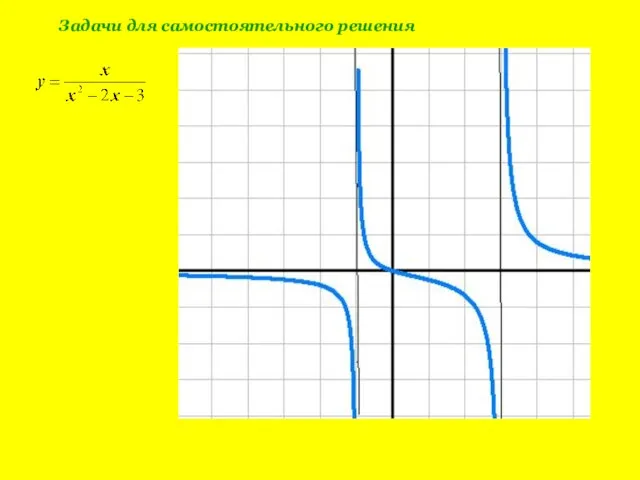
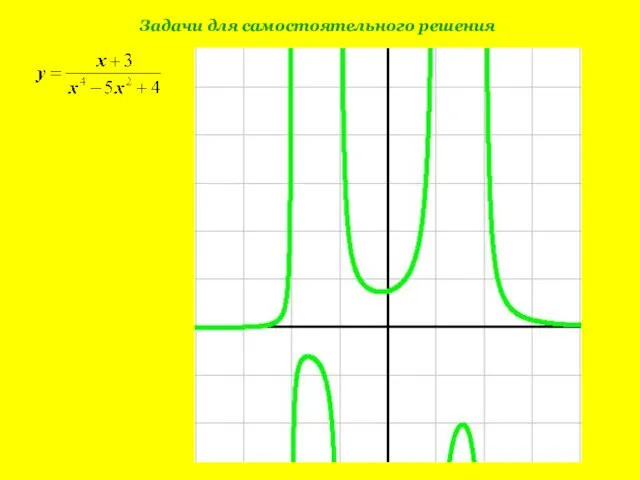
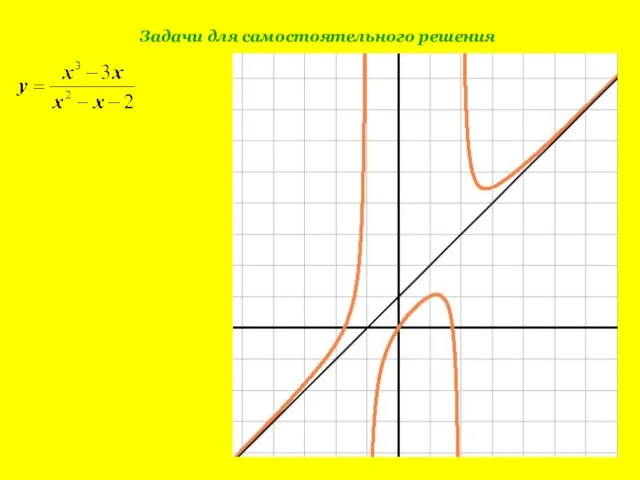
- 13. Задачи для самостоятельного решения
- 14. Задачи для самостоятельного решения
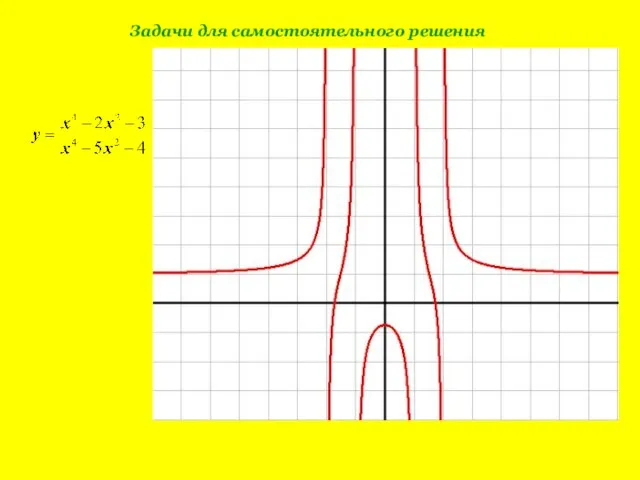
- 15. Задачи для самостоятельного решения
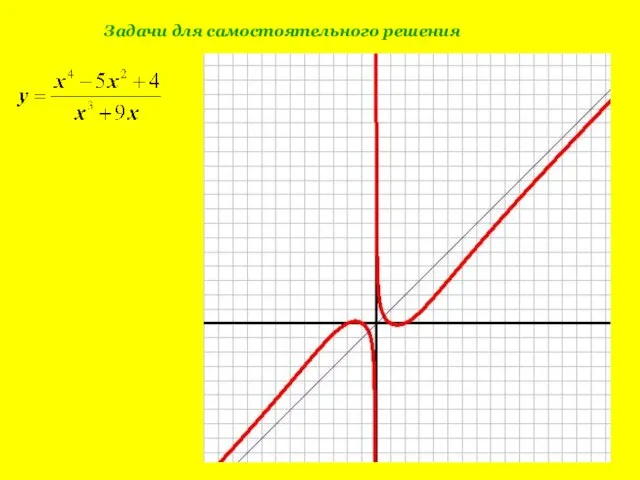
- 16. Задачи для самостоятельного решения
- 17. Задачи для самостоятельного решения
- 19. Скачать презентацию


 ЭкоПарковка (проекты)
ЭкоПарковка (проекты) Презентация на тему Логарифмы, логарифмическая функция
Презентация на тему Логарифмы, логарифмическая функция Экологизация школьного курса окружающего мира
Экологизация школьного курса окружающего мира Отношение сигнал помеха при корреляционном сравнении изображении
Отношение сигнал помеха при корреляционном сравнении изображении  История одной любви
История одной любви أساسيات اإلدارة
أساسيات اإلدارة Презентация на тему Правила поведения школьников во время зимних каникул
Презентация на тему Правила поведения школьников во время зимних каникул Perenos_krasnykh_liniy_v_avtokad
Perenos_krasnykh_liniy_v_avtokad Александр Невский (3 класс)
Александр Невский (3 класс) Спряжение глаголов. Закрепление
Спряжение глаголов. Закрепление Презентация на тему Мегалополисы мира
Презентация на тему Мегалополисы мира  Good laboratory practice
Good laboratory practice Планирование расходов в период подготовки и проведения выборов в единый день голосования
Планирование расходов в период подготовки и проведения выборов в единый день голосования Социальный конфликт и виды противоречий
Социальный конфликт и виды противоречий Презентация на тему: Шедевры Мировой архитектуры
Презентация на тему: Шедевры Мировой архитектуры группа Непоседы
группа Непоседы История коллажа
История коллажа Презентація
Презентація Создание поздравительной открытки
Создание поздравительной открытки Виктор Михайлович Васнецов
Виктор Михайлович Васнецов Презентация на тему Русская игрушка - Матрешка
Презентация на тему Русская игрушка - Матрешка Станок для обработки торцевой поверхности
Станок для обработки торцевой поверхности Эволюция телефона за 100 лет
Эволюция телефона за 100 лет Микропроцессор
Микропроцессор Искусство, 11 класс
Искусство, 11 класс Малые архитектурные сооружения в дизайне пришкольной территории
Малые архитектурные сооружения в дизайне пришкольной территории Объёмная снежинка из бумаги
Объёмная снежинка из бумаги ТЕМА УРОКА: АНАЛИЗ 1 ЧАСТИ ПОЭМЫ Н.А. НЕКРАСОВА «РУССКИЕ ЖЕНЩИНЫ». «И ПОДВИГ ВАШ БЕССМЕРТЕН …!» УЧИТЕЛЬ Зуева Людмила Василь
ТЕМА УРОКА: АНАЛИЗ 1 ЧАСТИ ПОЭМЫ Н.А. НЕКРАСОВА «РУССКИЕ ЖЕНЩИНЫ». «И ПОДВИГ ВАШ БЕССМЕРТЕН …!» УЧИТЕЛЬ Зуева Людмила Василь