Слайд 2Рішення задач повинно супроводжуватися короткими поясненнями і кресленнями, на яких всі розрахункові

величини слід вказати в числах, що відповідають власному варіанту. При використанні в розрахунках формул слід підставити в них числові значення і, не наводячи проміжних обчислень, записати відповідь із зазначенням розмірності визначених величин.
Якщо неправильно виконана робота повернута ЗВО для виправлення, то ці виправлення слід виконати на окремих аркушах, вкласти їх в не зараховану роботу і здати повторно на перевірку. Окремо від початкового варіанту розв’язку завдань розрахунково-графічної роботи виправлення не розглядаються.
Задачі оформляються у формі пояснювальної записки на аркушах формату А4 (297*210) згідно ДСТУ 3008-95. Документація. Звіти у сфері науки і техніки. Структура і правила оформлення. Звіт з виконання РГР включає:
Титульний аркуш;
Зміст (перелік всіх завдань із зазначенням сторінок);
Рішення задач;
Використані джерела.
Виконану і зараховану розрахунково-графічну роботу ЗВО повинен пред’явити на заліку або іспиті.
Критерії оцінювання виконання РГР наведені в таблиці нижче.
Зразки оформлення титульного та поточного аркушів наведено нижче.
Слайд 4Всі завдання розрахунково-графічної роботи повинні виконуватися за принципами академічної доброчесності. ЗВО повинні

ознайомитися з «Кодексом академічної доброчесності Національного університету «Чернігівська політехніка» (нова редакція)», затвердженого Вченою радою Національного університету «Чернігівська політехніка» 31 травня 2021 р. протокол № 5 та введеного в дію наказом ректора від 31 травня 2021 р. №100 (https://stu.cn.ua/wp-content/uploads/2021/06/kodeks-akademichnoyi-dobrochesnosti-nova-redakcziya.pdf).
Слайд 7Задача №1. Розрахунок статично визначуваних систем, які працюють на розтягання і стискання
Ступінчатий

брус завантажений силами F1, F2, F3, що напрямлені вздовж його осі. Задано довжини ділянок a, b, c і площі їх поперечних перерізів F1 і F2 . Модуль пружності матеріалу Е=2·105 МПа, границя текучості σТ =240 МПа і запас міцності відносно до межі текучості nТ =1,5.
Необхідно:
1) побудувати епюри повздовжніх сил N, напружень σ і повздовжніх переміщень Δ;
2) перевірити виконання умови міцності.
Розрахункові схеми вибираються за рис. 1, числові дані беруться з табл. 1.
Слайд 8Рис. 1. Розрахункові
схеми до
задачі № 1

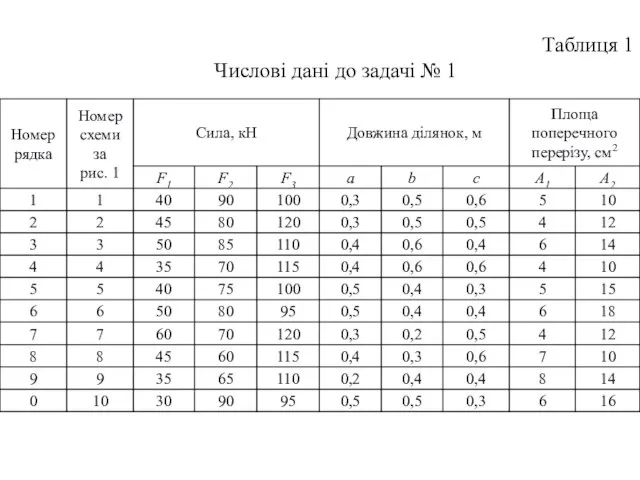
Слайд 9Таблиця 1
Числові дані до задачі № 1
Слайд 12Використовуючи співвідношення σmax≤[σ], яке називається умовою міцності за допустимими напруженнями, можна вирішити
![Використовуючи співвідношення σmax≤[σ], яке називається умовою міцності за допустимими напруженнями, можна вирішити](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/914038/slide-11.jpg)
три основні задачі опору матеріалів:
1. Підібрати переріз розтягнутого (стиснутого) бруса, при якому його міцність буде забезпечена. Розрахункова формула в цьому випадку має вигляд
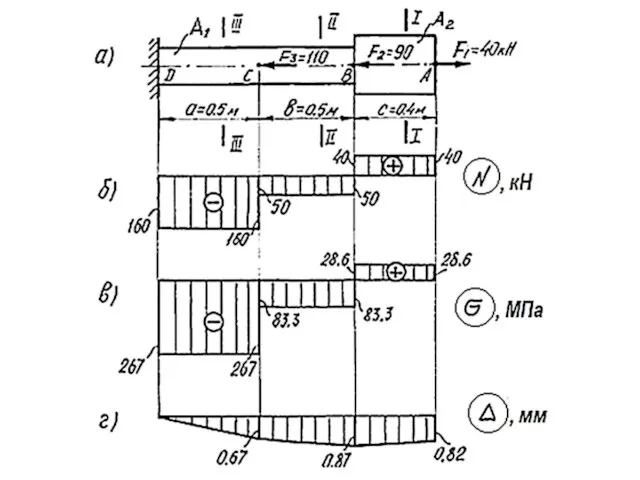
Слайд 16Рис. 2. Розрахункова схема бруса та епюри:
а) – розрахункова схема; б) –
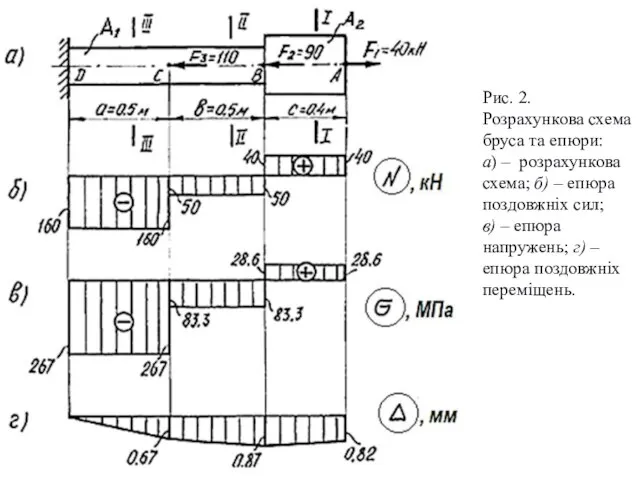
епюра поздовжніх сил;
в) – епюра напружень; г) –епюра поздовжніх переміщень.
Слайд 18Приклад вибору масштабу для побудови епюри N
1) Нехай 100 кН відповідає відрізок
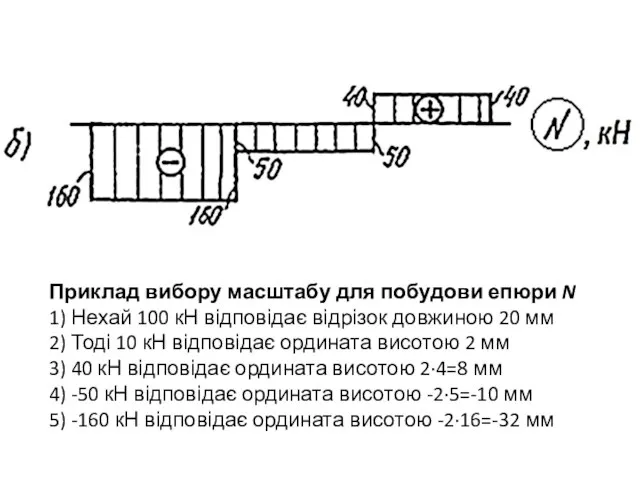
довжиною 20 мм
2) Тоді 10 кН відповідає ордината висотою 2 мм
3) 40 кН відповідає ордината висотою 2·4=8 мм
4) -50 кН відповідає ордината висотою -2·5=-10 мм
5) -160 кН відповідає ордината висотою -2·16=-32 мм
Слайд 20Приклад вибору масштабу для побудови епюри σ
1) Нехай 100 МПа відповідає відрізок
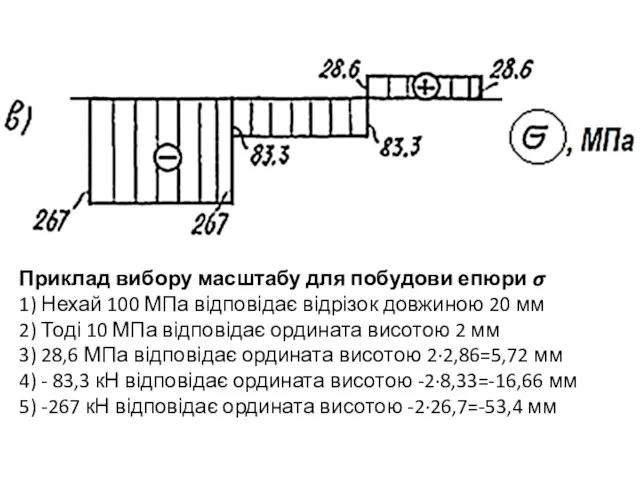
довжиною 20 мм
2) Тоді 10 МПа відповідає ордината висотою 2 мм
3) 28,6 МПа відповідає ордината висотою 2·2,86=5,72 мм
4) - 83,3 кН відповідає ордината висотою -2·8,33=-16,66 мм
5) -267 кН відповідає ордината висотою -2·26,7=-53,4 мм
Слайд 23Приклад вибору масштабу для побудови епюри Δ
1) Нехай Δ=1 мм відповідає відрізок
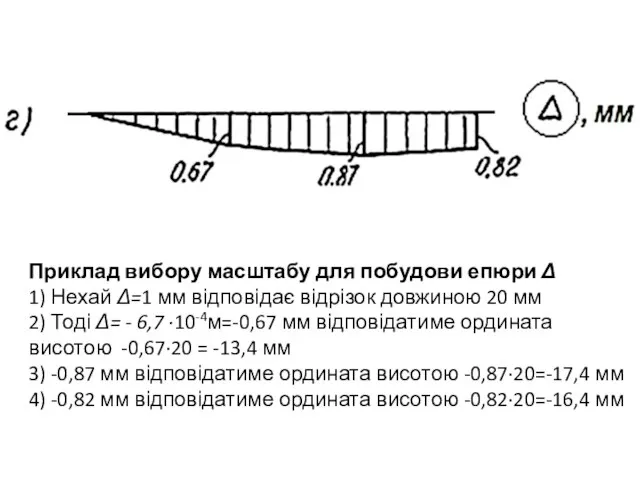
довжиною 20 мм
2) Тоді Δ= - 6,7 ·10-4м=-0,67 мм відповідатиме ордината висотою -0,67·20 = -13,4 мм
3) -0,87 мм відповідатиме ордината висотою -0,87·20=-17,4 мм
4) -0,82 мм відповідатиме ордината висотою -0,82·20=-16,4 мм










![Використовуючи співвідношення σmax≤[σ], яке називається умовою міцності за допустимими напруженнями, можна вирішити](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/914038/slide-11.jpg)











 ( 1998гг.11лет )
( 1998гг.11лет ) Новый взгляд на трансляции спортивных мероприятий. VR-Sport
Новый взгляд на трансляции спортивных мероприятий. VR-Sport Забруднення Світового океану
Забруднення Світового океану Типовые конструкции изделия и узлы зданий и сооружений. Серия 1.020
Типовые конструкции изделия и узлы зданий и сооружений. Серия 1.020 Сибирская язва
Сибирская язва Тундра
Тундра Предпринимательское право
Предпринимательское право УПРАВЛЕНИЕ ВВЕДЕНИЕМ ФГОСв МОУ «Средняя общеобразовательная школа №3» г.Сорочинска2010-2012 учебные годы
УПРАВЛЕНИЕ ВВЕДЕНИЕМ ФГОСв МОУ «Средняя общеобразовательная школа №3» г.Сорочинска2010-2012 учебные годы Цели и задачи классного часа Цель: Показать учащимся значение сотрудничества стран, входящих в состав Содружества Независимых Гос
Цели и задачи классного часа Цель: Показать учащимся значение сотрудничества стран, входящих в состав Содружества Независимых Гос Презентация на тему Легенды и предания туманного Альбиона о рыцарях Круглого стола короля Артура
Презентация на тему Легенды и предания туманного Альбиона о рыцарях Круглого стола короля Артура  Презентация на тему Занимательное правоведение
Презентация на тему Занимательное правоведение  Прекрасное как основная этическая категория
Прекрасное как основная этическая категория Периодическая система химических элементов в почтовых марках.
Периодическая система химических элементов в почтовых марках. Ковалевская Софья Васильевна (1850–1891)
Ковалевская Софья Васильевна (1850–1891) Видеопрезентация учителя французского языка Тутаевой Елены Николаевны
Видеопрезентация учителя французского языка Тутаевой Елены Николаевны Әлифба
Әлифба Квест. Форма активного взаимодействия
Квест. Форма активного взаимодействия Мотивация клиента и цели менеджеров
Мотивация клиента и цели менеджеров Стратегия продаж в Росатом
Стратегия продаж в Росатом Явления природы
Явления природы Презентация на тему Брак и семья
Презентация на тему Брак и семья СТРУКТУРА КУРСА ФИЗИКИ
СТРУКТУРА КУРСА ФИЗИКИ Причины повреждения технологического оборудования
Причины повреждения технологического оборудования  Наградная система России часть 2 «Ордена СССР»
Наградная система России часть 2 «Ордена СССР» Кейсы - необходимый элемент образования
Кейсы - необходимый элемент образования Рокфеллер-центр в Нью-Йорке
Рокфеллер-центр в Нью-Йорке Система обеспечения эффективности, безопасности и качества фармацевтической
Система обеспечения эффективности, безопасности и качества фармацевтической ПАО Магнитогорский металлургический комбинат
ПАО Магнитогорский металлургический комбинат