Содержание
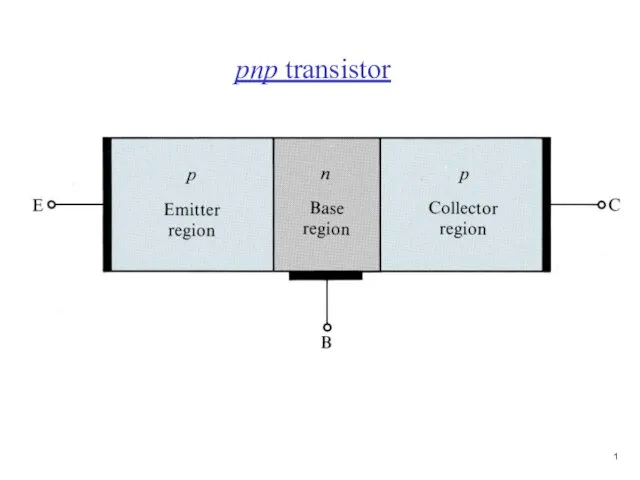
- 2. pnp transistor
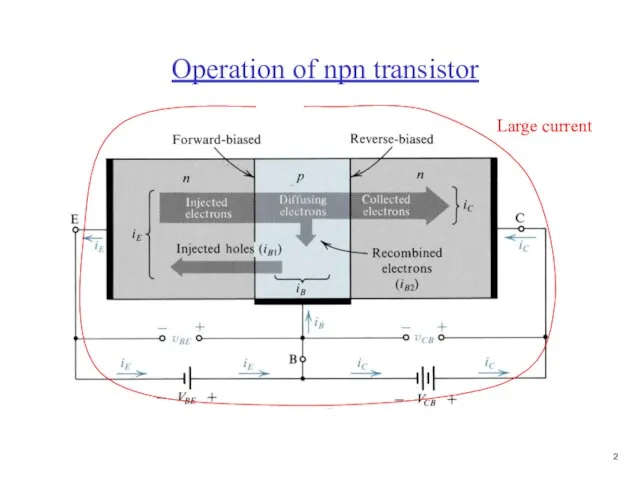
- 3. Large current Operation of npn transistor
- 4. Modes of operation of a BJT transistor Mode BE junction BC junction cutoff reverse biased reverse
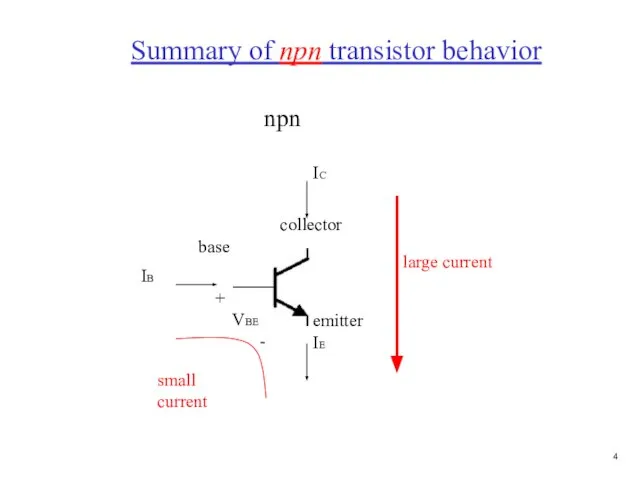
- 5. Summary of npn transistor behavior
- 6. Summary of pnp transistor behavior
- 7. Summary of equations for a BJT IE ≈ IC IC = βIB β is the current
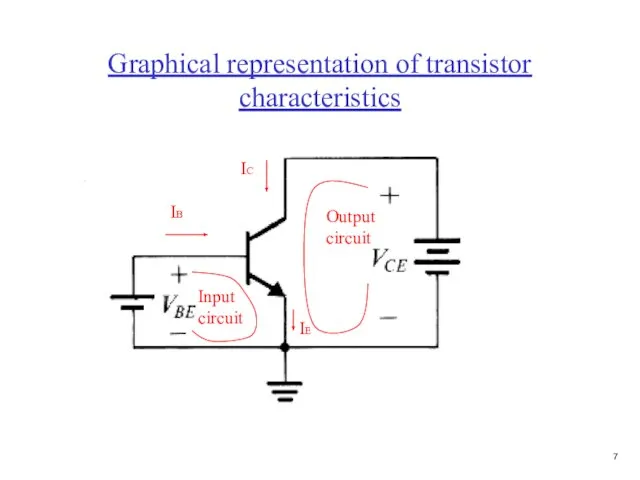
- 8. Graphical representation of transistor characteristics IB IC IE Output circuit Input circuit
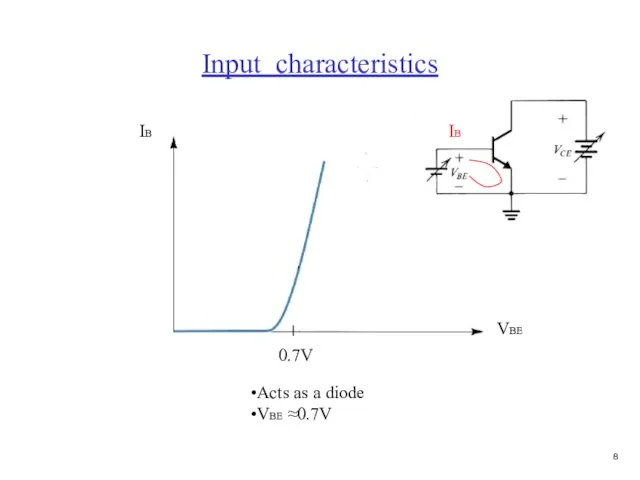
- 9. Input characteristics Acts as a diode VBE ≈0.7V IB IB VBE 0.7V
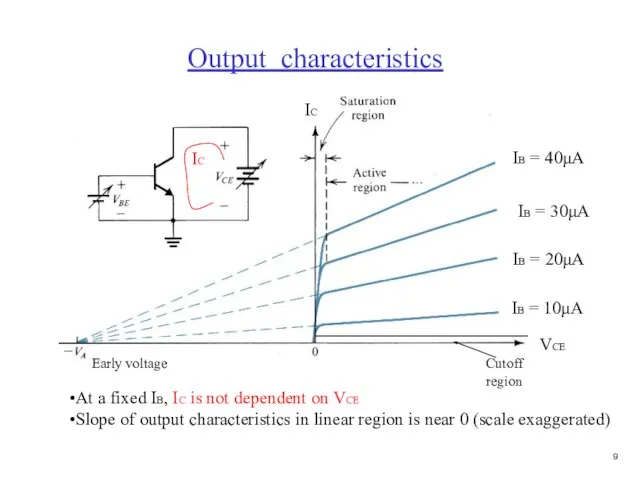
- 10. Output characteristics IC IC VCE IB = 10μA IB = 20μA IB = 30μA IB =
- 11. Biasing a transistor We must operate the transistor in the linear region. A transistor’s operating point
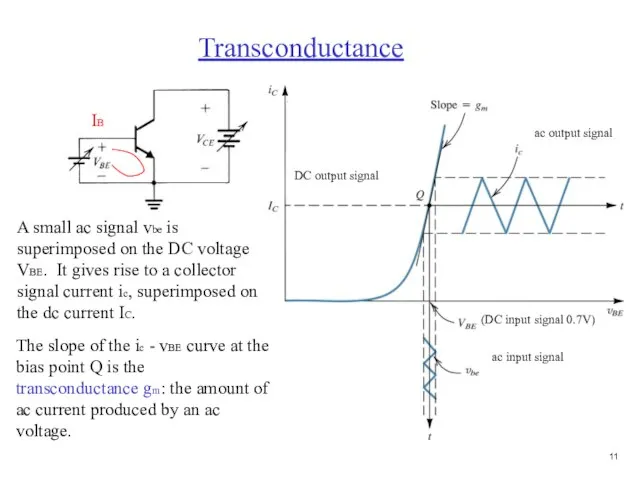
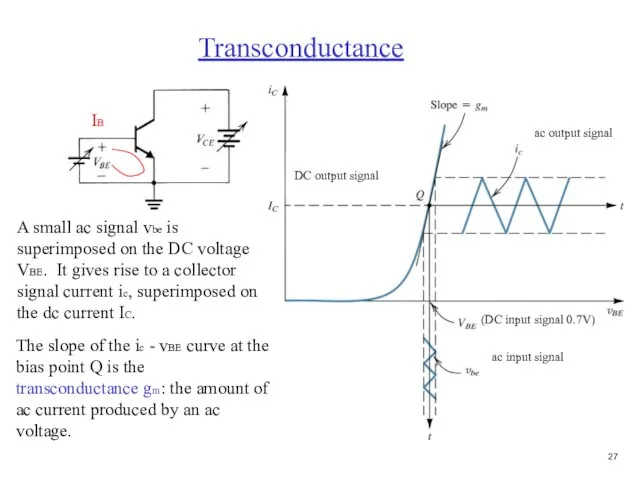
- 12. A small ac signal vbe is superimposed on the DC voltage VBE. It gives rise to
- 13. Analysis of transistor circuits at DC For all circuits: assume transistor operates in linear region write
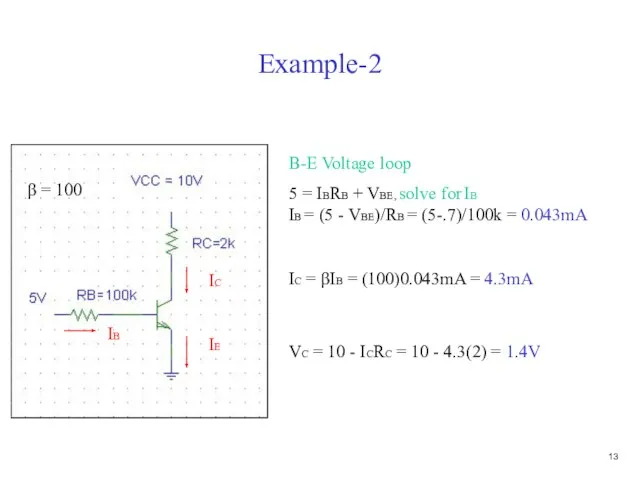
- 14. Example-2 B-E Voltage loop 5 = IBRB + VBE, solve for IB IB = (5 -
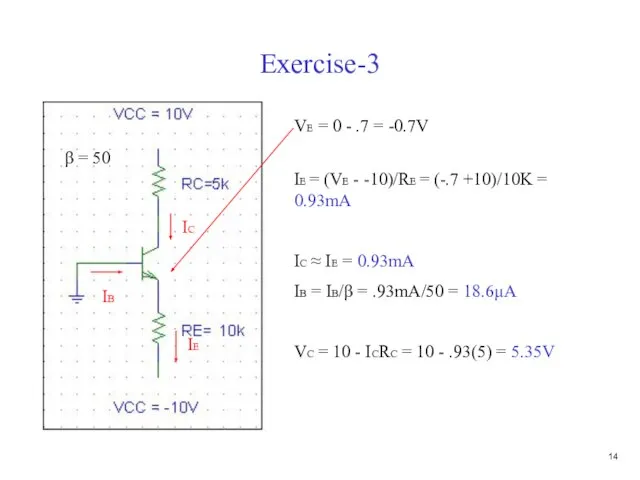
- 15. Exercise-3 VE = 0 - .7 = -0.7V IE IC IB β = 50 IE =
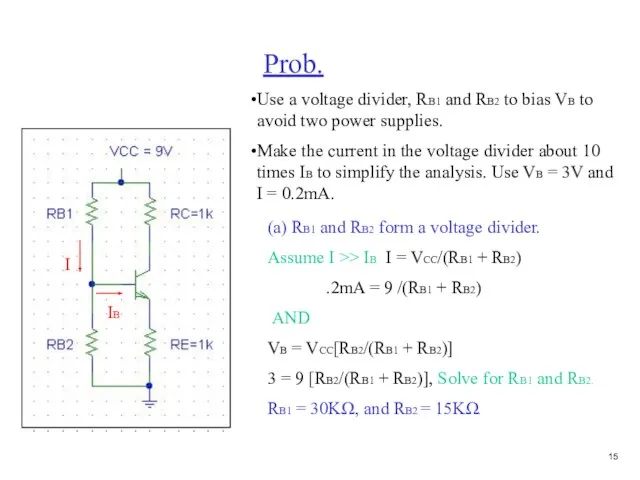
- 16. Prob. Use a voltage divider, RB1 and RB2 to bias VB to avoid two power supplies.
- 17. Prob. Find the operating point Use the Thevenin equivalent circuit for the base Makes the circuit
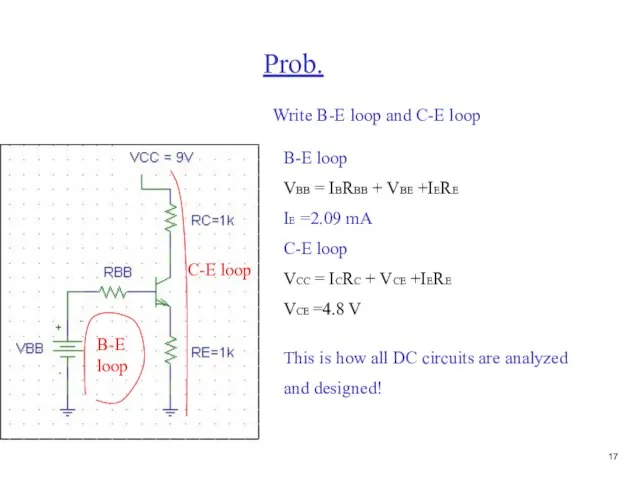
- 18. Prob. Write B-E loop and C-E loop B-E loop C-E loop B-E loop VBB = IBRBB
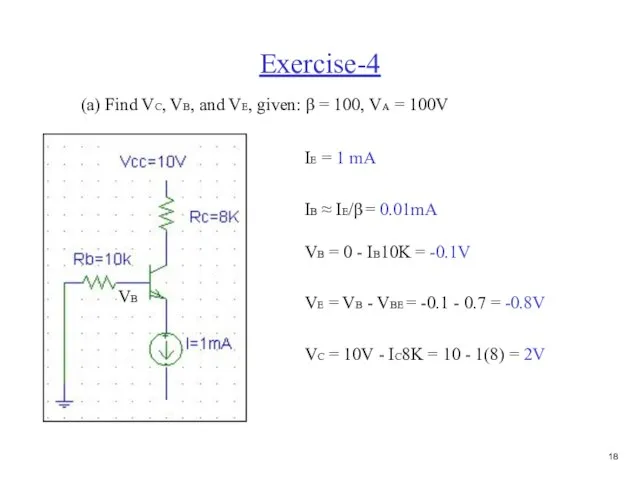
- 19. Exercise-4 (a) Find VC, VB, and VE, given: β = 100, VA = 100V IE =
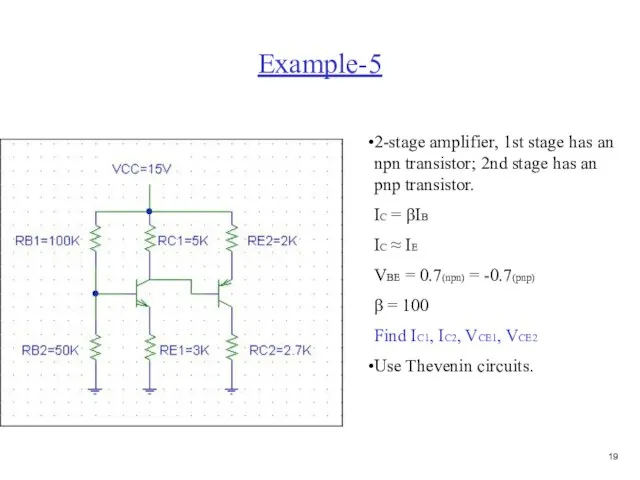
- 20. Example-5 2-stage amplifier, 1st stage has an npn transistor; 2nd stage has an pnp transistor. IC
- 21. Example -5 RBB1 = RB1||RB2 = 33K VBB1 = VCC[RB2/(RB1+RB2)] VBB1 = 15[50K/150K] = 5V Stage
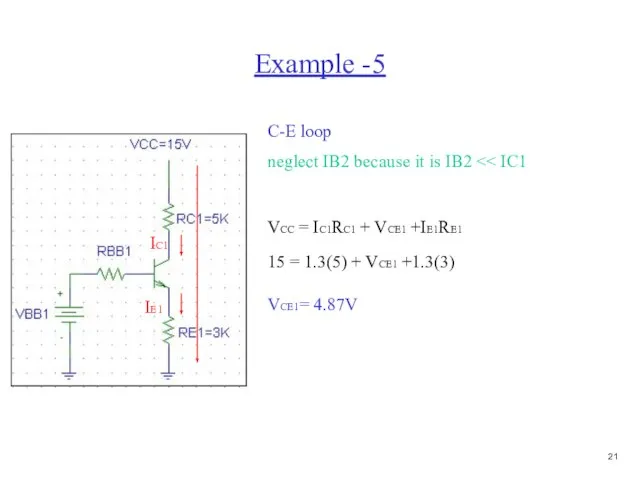
- 22. Example -5 C-E loop neglect IB2 because it is IB2 IE1 IC1 VCC = IC1RC1 +
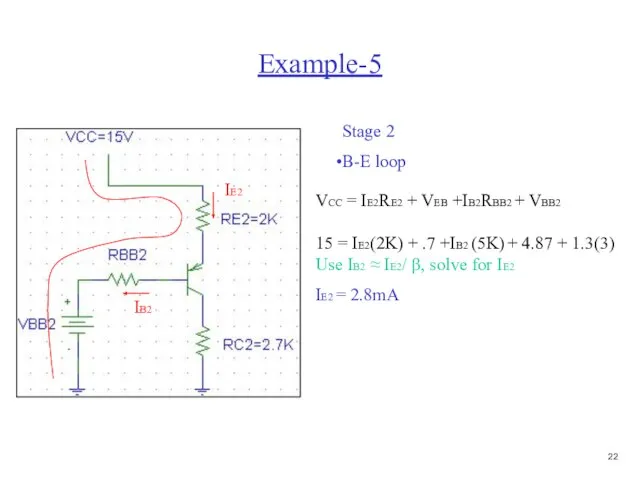
- 23. Example-5 Stage 2 B-E loop IB2 IE2 VCC = IE2RE2 + VEB +IB2RBB2 + VBB2 15
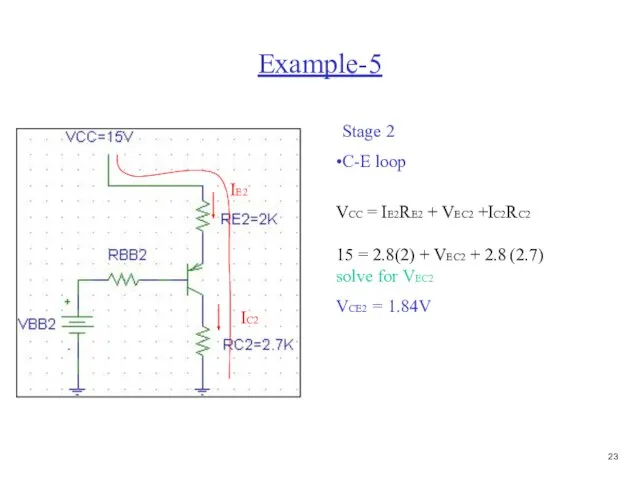
- 24. Example-5 Stage 2 C-E loop IE2 IC2 VCC = IE2RE2 + VEC2 +IC2RC2 15 = 2.8(2)
- 25. Summary of DC problem Bias transistors so that they operate in the linear region B-E junction
- 26. Summary of npn transistor behavior npn collector emitter base IB IE IC small current large current
- 27. Transistor as an amplifier Transistor circuits are analyzed and designed in terms of DC and ac
- 28. A small ac signal vbe is superimposed on the DC voltage VBE. It gives rise to
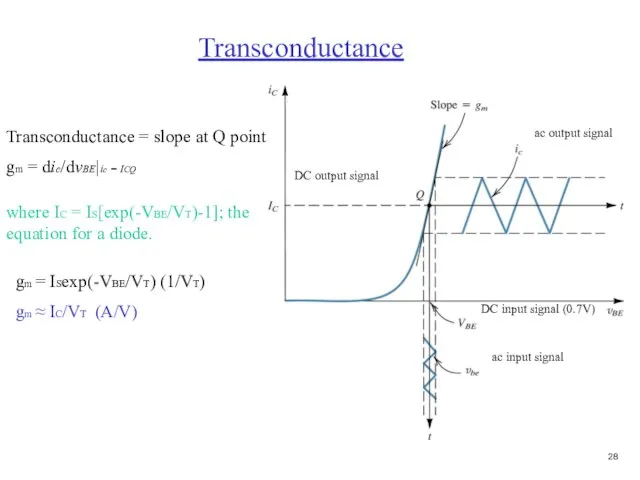
- 29. Transconductance = slope at Q point gm = dic/dvBE|ic = ICQ where IC = IS[exp(-VBE/VT)-1]; the
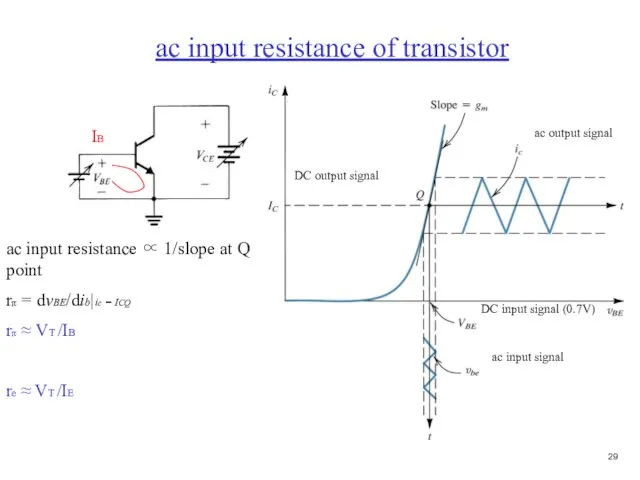
- 30. ac input resistance ∝ 1/slope at Q point rπ = dvBE/dib|ic = ICQ rπ ≈ VT
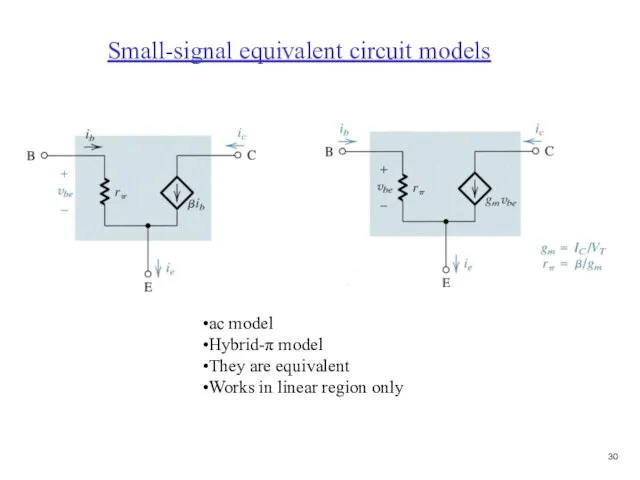
- 31. Small-signal equivalent circuit models ac model Hybrid-π model They are equivalent Works in linear region only
- 32. Steps to analyze a transistor circuit 1 DC problem Set ac sources to zero, solve for
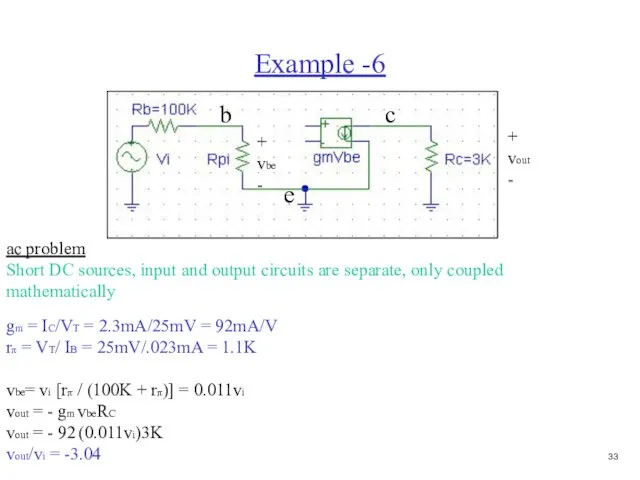
- 33. Example-6 Find vout/vin, (β = 100) DC problem Short vi, determine IC and VCE B-E voltage
- 34. Example -6 ac problem Short DC sources, input and output circuits are separate, only coupled mathematically
- 35. Exercise-7 Find gm, rπ, and r0, given: β = 100, VA = 100V,IC=1 mA gm =
- 36. Summary of transistor analysis Transistor circuits are analyzed and designed in terms of DC and ac
- 37. Steps to analyze a transistor circuit 1 DC Analysis Set ac sources to zero, solve for
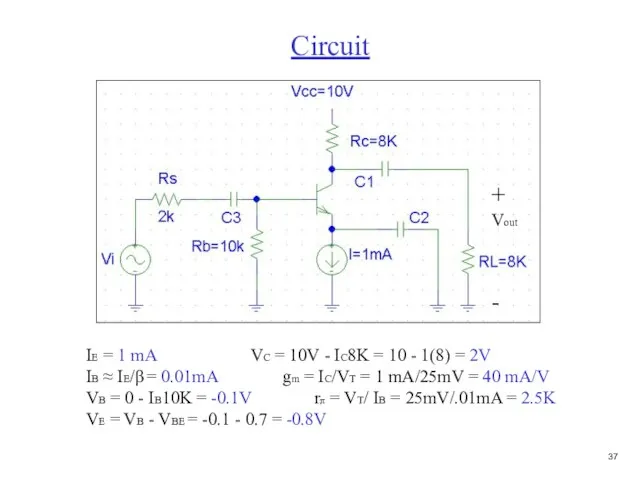
- 38. Circuit IE = 1 mA VC = 10V - IC8K = 10 - 1(8) = 2V
- 39. ac equivalent circuit b e c vbe = (Rb||Rpi)/ [(Rb||Rpi) +Rs]vi vbe = 0.5vi vout =
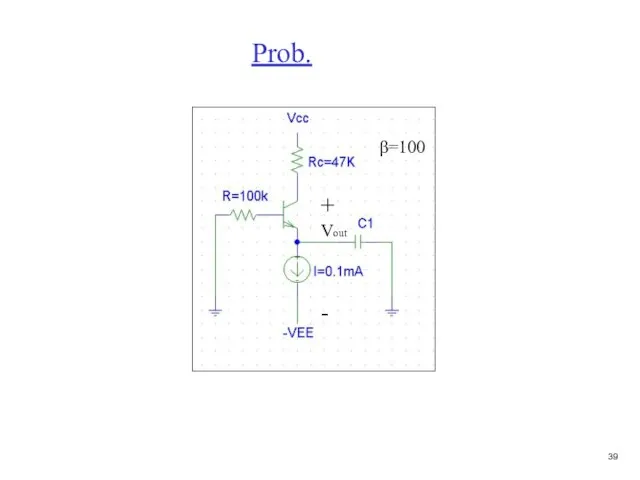
- 40. Prob. + Vout - β=100
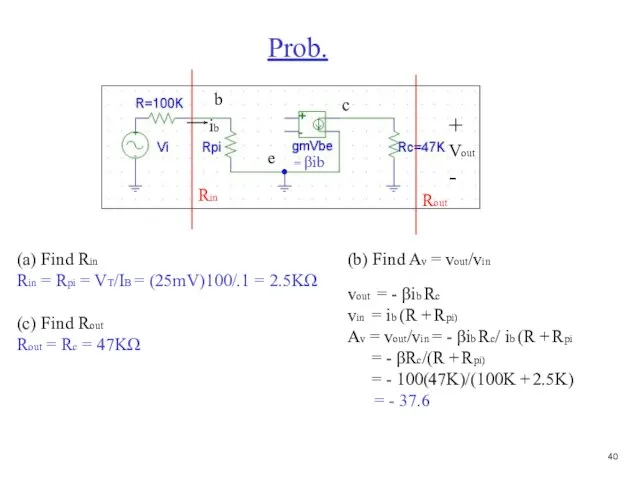
- 41. Prob. + Vout - (a) Find Rin Rin = Rpi = VT/IB = (25mV)100/.1 = 2.5KΩ
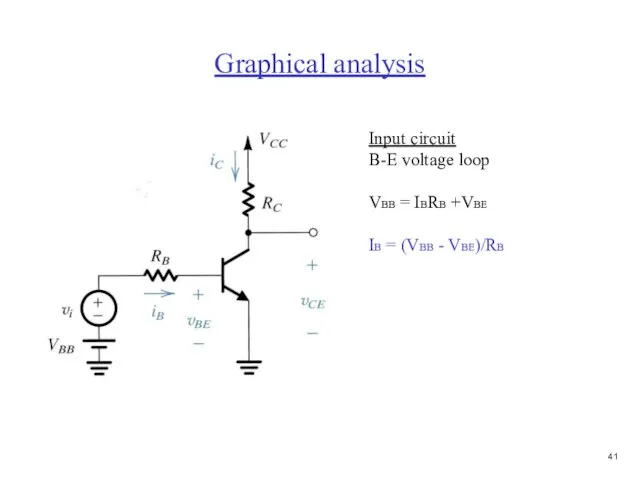
- 42. Graphical analysis Input circuit B-E voltage loop VBB = IBRB +VBE IB = (VBB - VBE)/RB
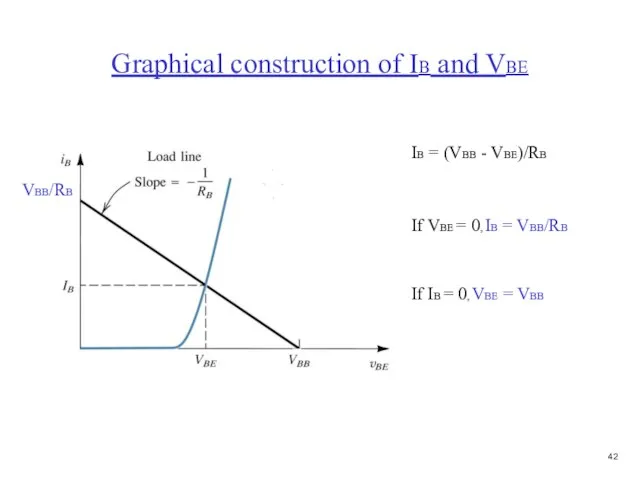
- 43. Graphical construction of IB and VBE IB = (VBB - VBE)/RB If VBE = 0, IB
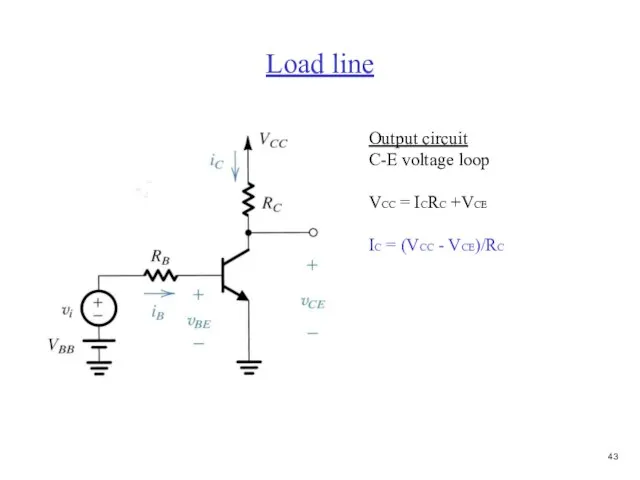
- 44. Load line Output circuit C-E voltage loop VCC = ICRC +VCE IC = (VCC - VCE)/RC
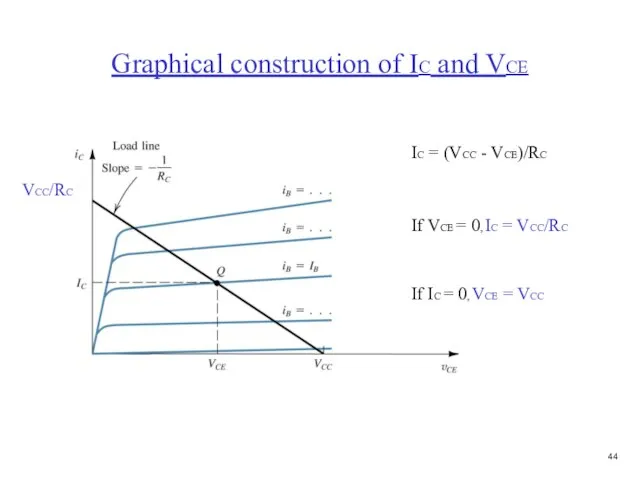
- 45. Graphical construction of IC and VCE VCC/RC IC = (VCC - VCE)/RC If VCE = 0,
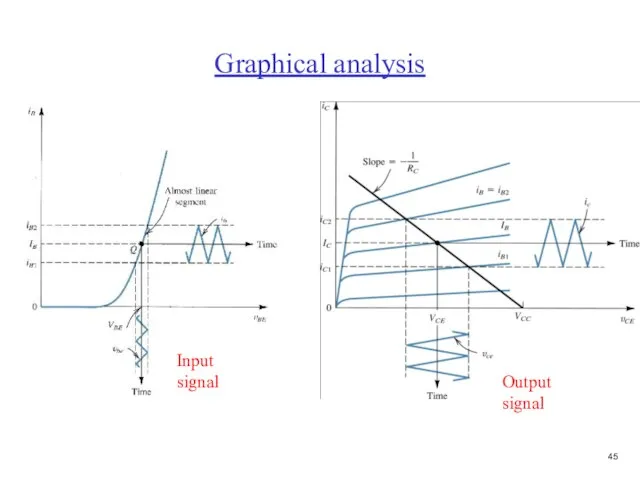
- 46. Graphical analysis Input signal Output signal
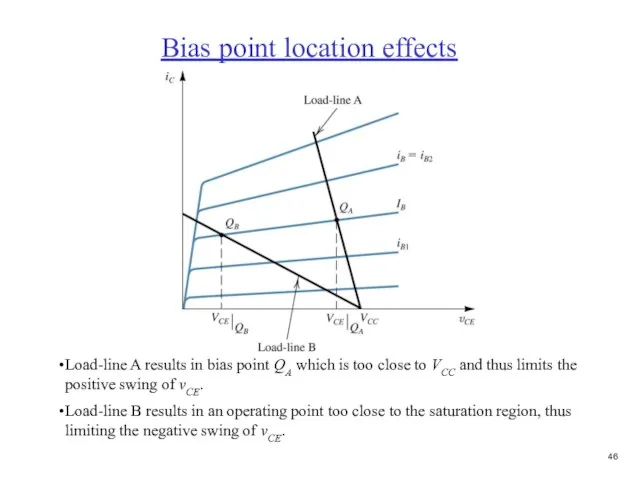
- 47. Load-line A results in bias point QA which is too close to VCC and thus limits
- 48. Basic single-stage BJT amplifier configurations We will study 3 types of BJT amplifiers CE - common
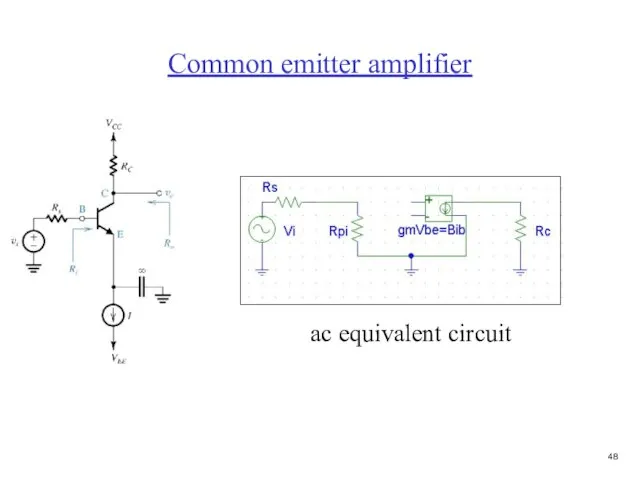
- 49. Common emitter amplifier ac equivalent circuit
- 50. Common emitter amplifier Rin Rout + Vout - Rin (Does not include source) Rin = Rpi
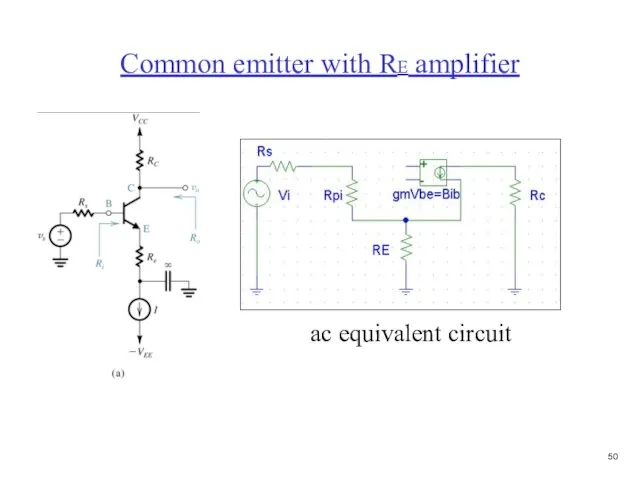
- 51. Common emitter with RE amplifier ac equivalent circuit
- 52. Common emitter with RE amplifier Rin Rout + Vout - Rin Rin = V/ib V =
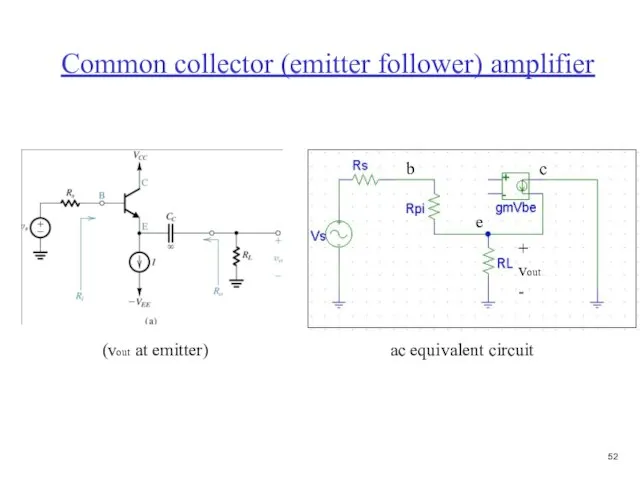
- 53. Common collector (emitter follower) amplifier b c e + vout - (vout at emitter) ac equivalent
- 54. Common collector amplifier Rin + vout - Rin Rin = V/ib V = ib Rpi +
- 55. Common collector amplifier Rout + vout - Rout (don’t include RL, set Vs = 0) Rout
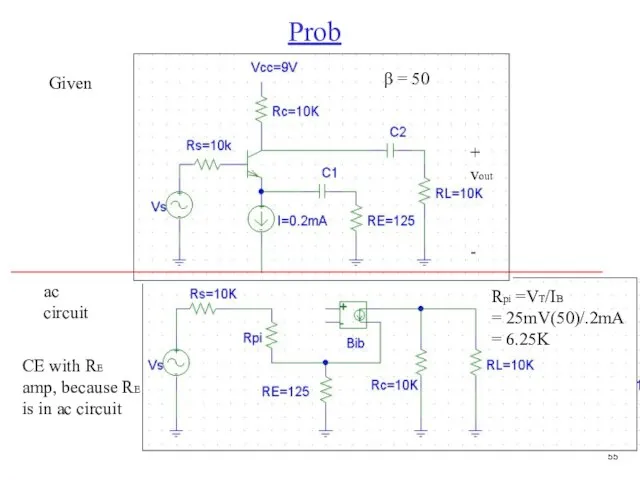
- 56. Prob ac circuit CE with RE amp, because RE is in ac circuit Given Rpi =VT/IB
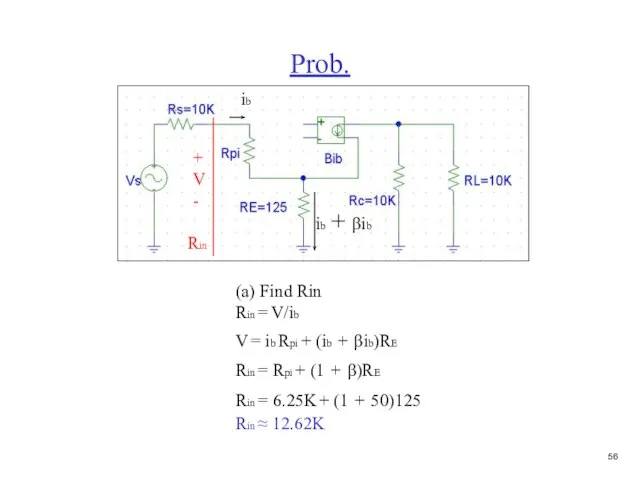
- 57. Prob. (a) Find Rin Rin = V/ib V = ib Rpi + (ib + βib)RE Rin
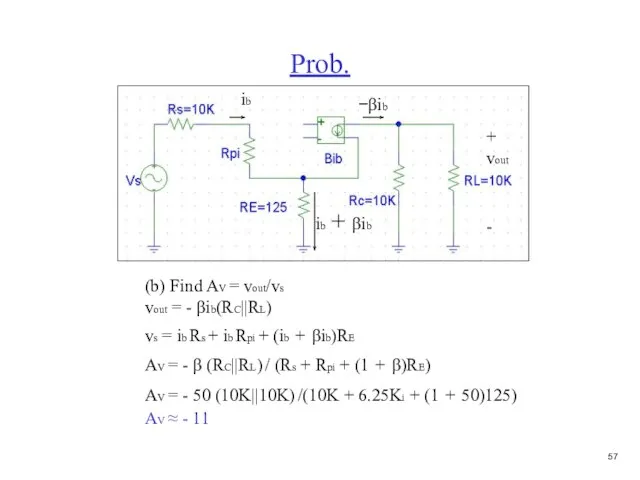
- 58. Prob. (b) Find AV = vout/vs vout = - βib(RC||RL) vs = ib Rs + ib
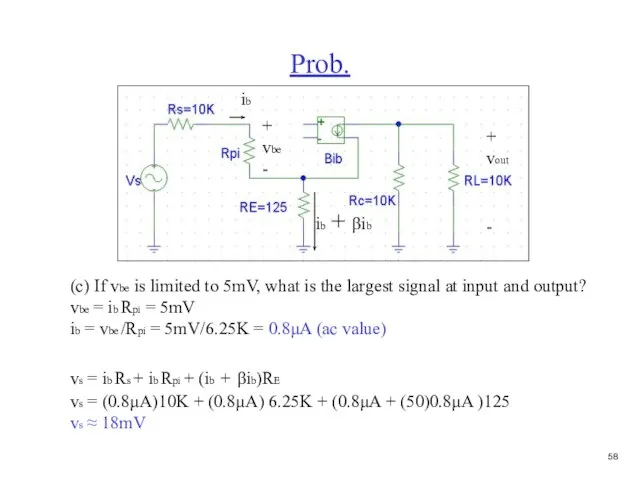
- 59. Prob. (c) If vbe is limited to 5mV, what is the largest signal at input and
- 60. Prob. (c) If vbe is limited to 5mV, what is the largest signal at input and
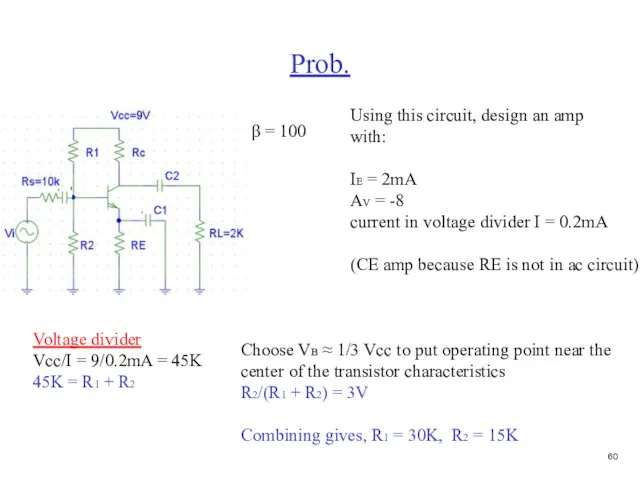
- 61. Prob. Using this circuit, design an amp with: IE = 2mA AV = -8 current in
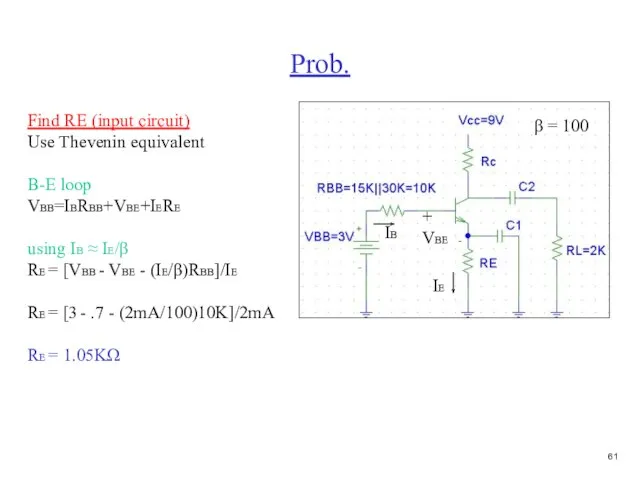
- 62. Prob. β = 100 Find RE (input circuit) Use Thevenin equivalent B-E loop VBB=IBRBB+VBE+IERE using IB
- 63. Prob. Find Rc (ac circuit) Rpi = VT/IB = 25mV(100)/2mA = 1.25K Ro = VA/IC =
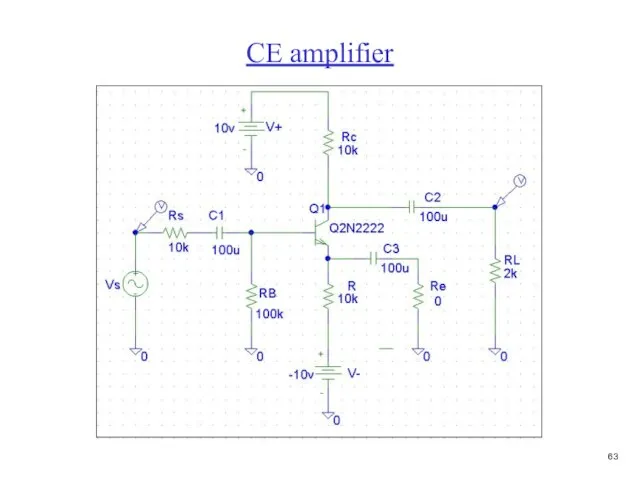
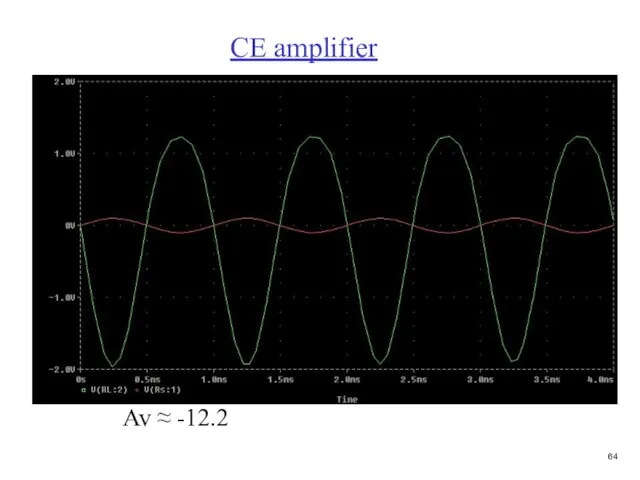
- 64. CE amplifier
- 65. CE amplifier Av ≈ -12.2
- 66. FOURIER COMPONENTS OF TRANSIENT RESPONSE V($N_0009) DC COMPONENT = -1.226074E-01 HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED
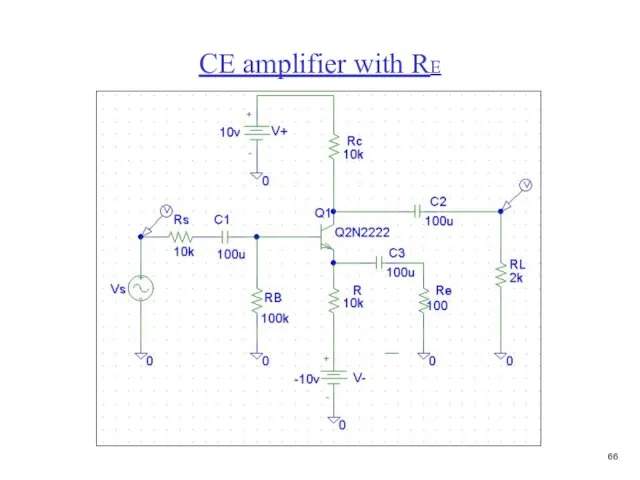
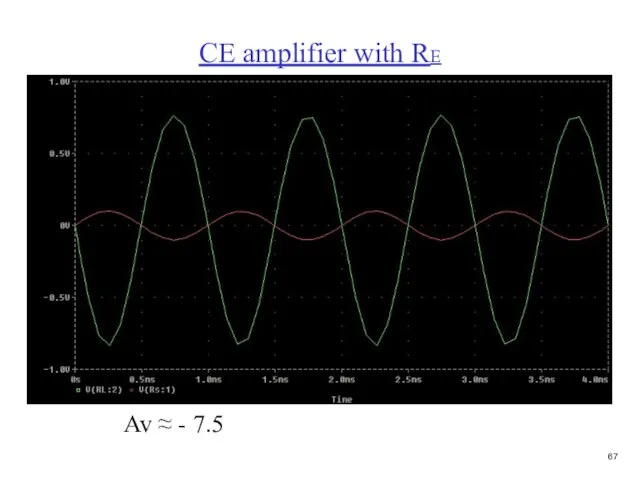
- 67. CE amplifier with RE
- 68. CE amplifier with RE Av ≈ - 7.5
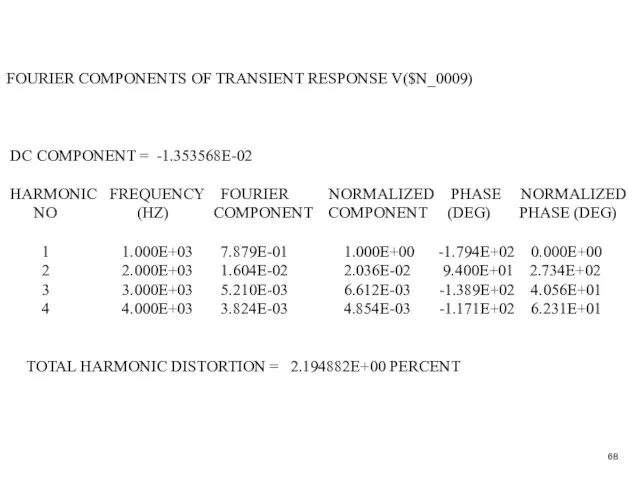
- 69. FOURIER COMPONENTS OF TRANSIENT RESPONSE V($N_0009) DC COMPONENT = -1.353568E-02 HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED
- 70. Summary Av THD CE -12.2 12.7% CE w/RE (RE = 100) -7.5 2.19%
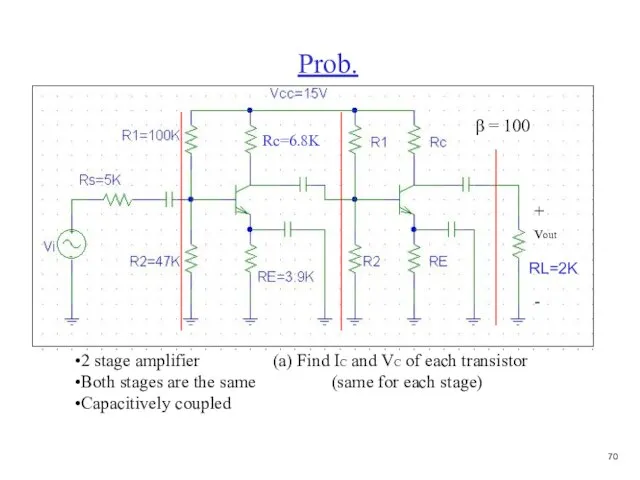
- 71. Prob. + vout - 2 stage amplifier (a) Find IC and VC of each transistor Both
- 72. Prob. (a) Find IC and VC of each transistor (same for each stage) B-E voltage loop
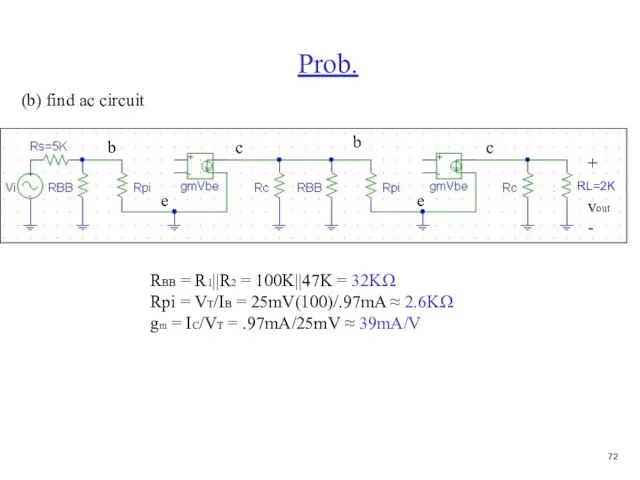
- 73. Prob. b c e + vout - (b) find ac circuit b c e RBB =
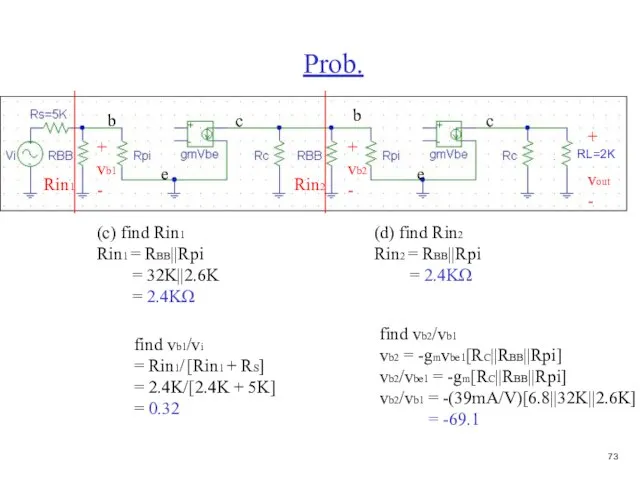
- 74. Prob. b c e + vout - (c) find Rin1 Rin1 = RBB||Rpi = 32K||2.6K =
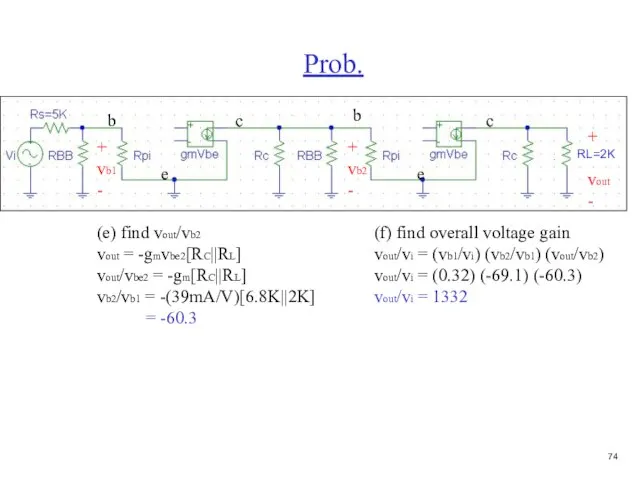
- 75. Prob. b c e + vout - (e) find vout/vb2 vout = -gmvbe2[RC||RL] vout/vbe2 = -gm[RC||RL]
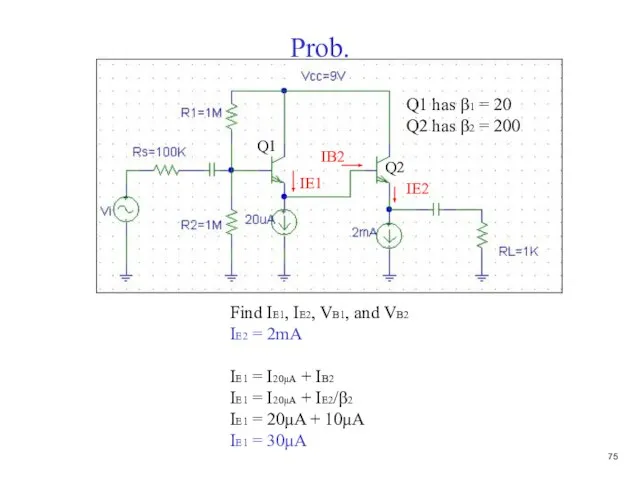
- 76. Prob. Find IE1, IE2, VB1, and VB2 IE2 = 2mA IE1 = I20μA + IB2 IE1
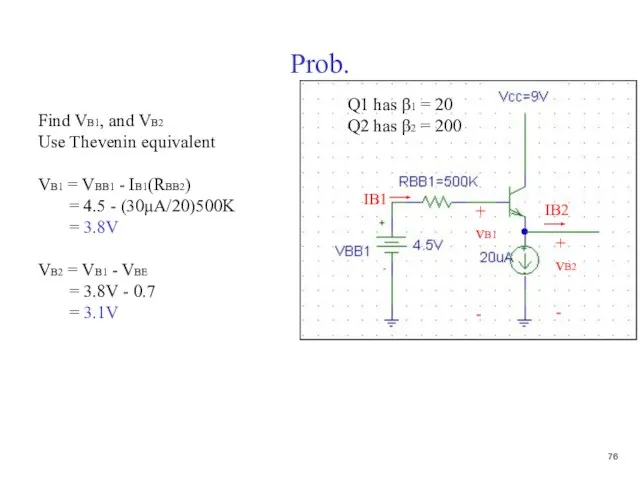
- 77. Prob. Find VB1, and VB2 Use Thevenin equivalent VB1 = VBB1 - IB1(RBB2) = 4.5 -
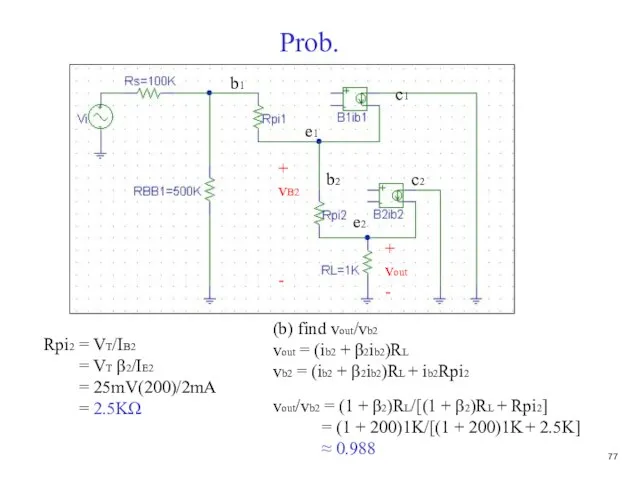
- 78. Prob. (b) find vout/vb2 vout = (ib2 + β2ib2)RL vb2 = (ib2 + β2ib2)RL + ib2Rpi2
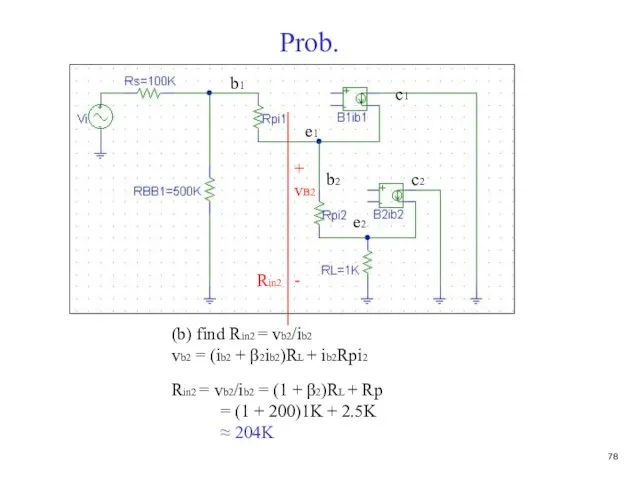
- 79. Prob. (b) find Rin2 = vb2/ib2 vb2 = (ib2 + β2ib2)RL + ib2Rpi2 Rin2 = vb2/ib2
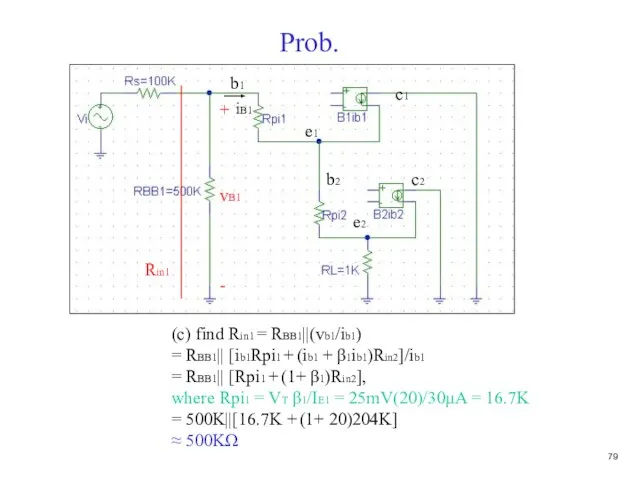
- 80. Prob. (c) find Rin1 = RBB1||(vb1/ib1) = RBB1|| [ib1Rpi1 + (ib1 + β1ib1)Rin2]/ib1 = RBB1|| [Rpi1
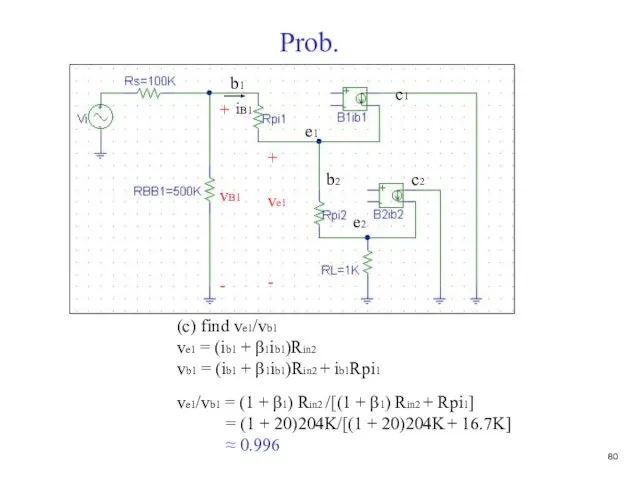
- 81. Prob. (c) find ve1/vb1 ve1 = (ib1 + β1ib1)Rin2 vb1 = (ib1 + β1ib1)Rin2 + ib1Rpi1
- 82. Prob. (d) find vb1/vi vb1/vi = Rin1/[RS + Rin1] = 0.82 b1 e1 c1 b2 e2
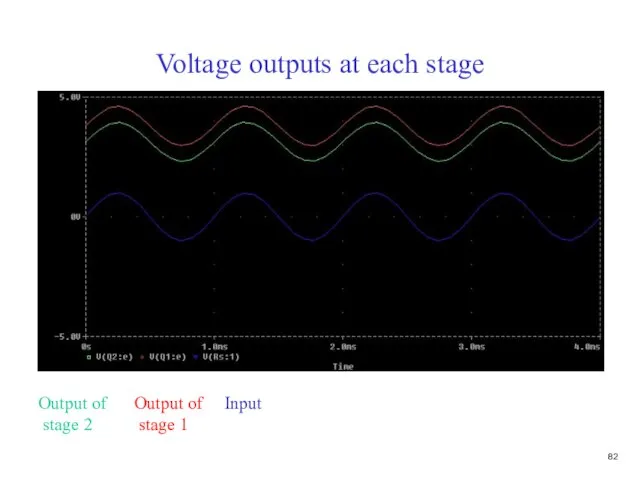
- 83. Voltage outputs at each stage Output of stage 2 Output of stage 1 Input
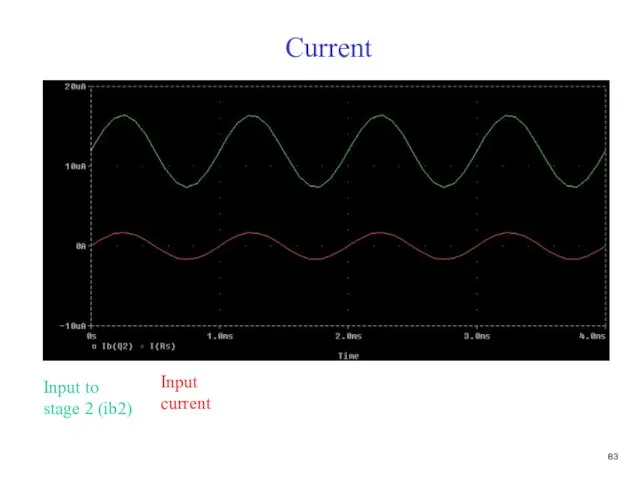
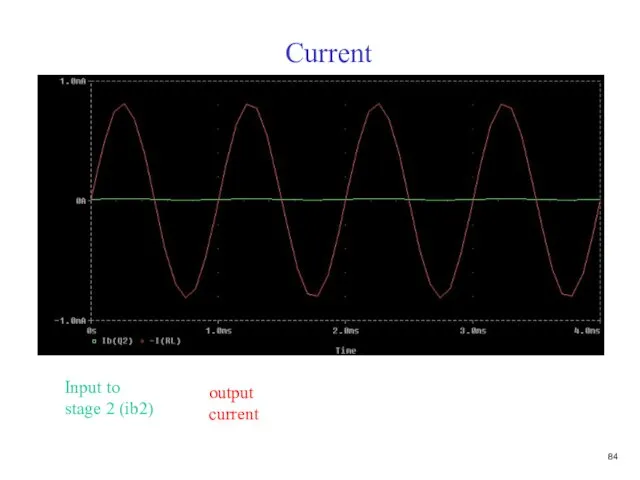
- 84. Current Input current Input to stage 2 (ib2)
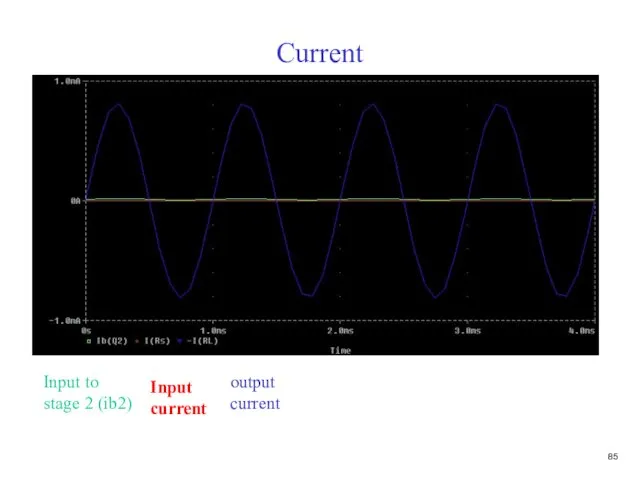
- 85. Current output current Input to stage 2 (ib2)
- 86. Current output current Input to stage 2 (ib2) Input current
- 87. Power and current gain Input current = (Vi)/Rin = 1/500K = 2.0μA output current= (Vout)/RL =
- 88. BJT Output Characteristics Plot Ic vs. Vce for multiple values of Vce and Ib From Analysis
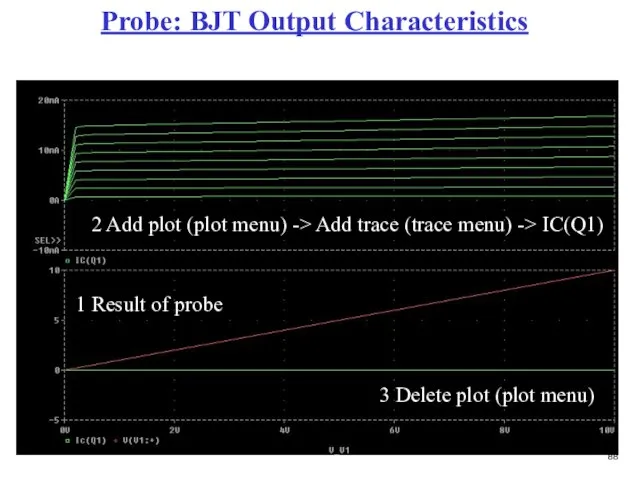
- 89. Probe: BJT Output Characteristics 1 Result of probe 2 Add plot (plot menu) -> Add trace
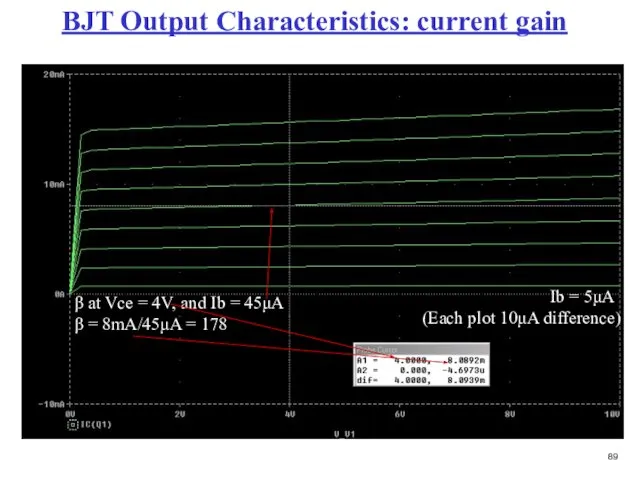
- 90. BJT Output Characteristics: current gain Ib = 5μA (Each plot 10μA difference) β at Vce =
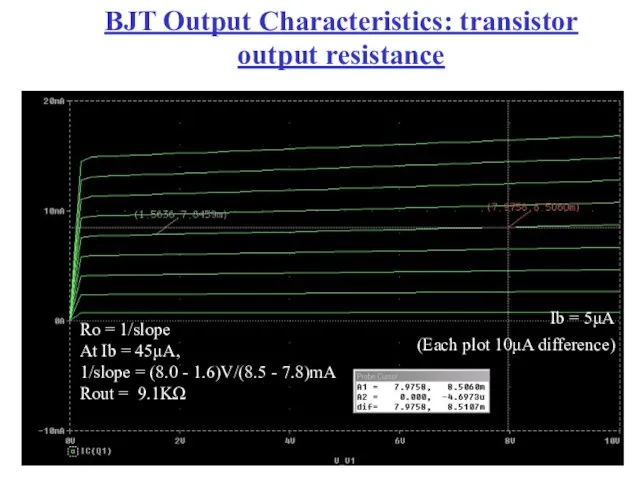
- 91. BJT Output Characteristics: transistor output resistance Ib = 5μA (Each plot 10μA difference) Ro = 1/slope
- 92. CE Amplifier: Measurements with Spice Rin Rout
- 93. Input Resistance Measurement Using SPICE Replace source, Vs and Rs with Vin, measure Rin = Vin/Iin
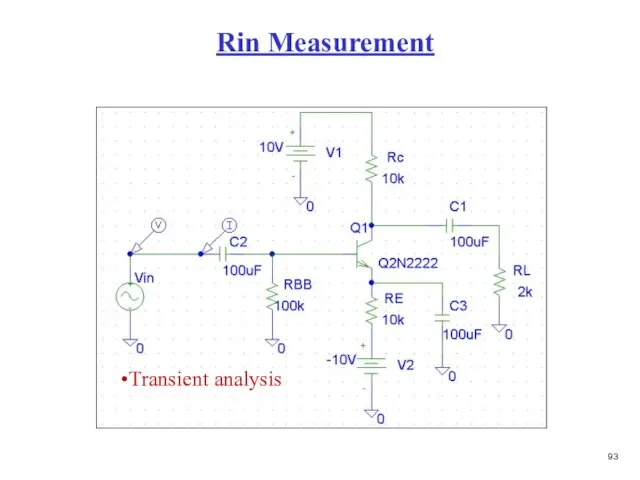
- 94. Rin Measurement Transient analysis
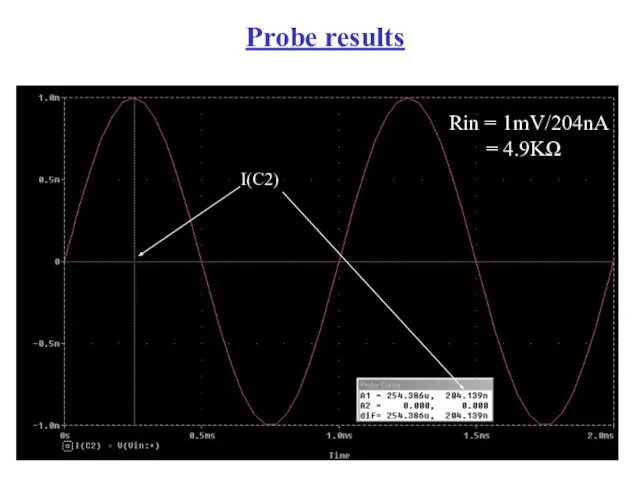
- 95. Probe results I(C2) Rin = 1mV/204nA = 4.9KΩ
- 96. Output Resistance Measurement Using SPICE Replace load, RL with Vin, measure Rin = Vin/Iin Set Vs
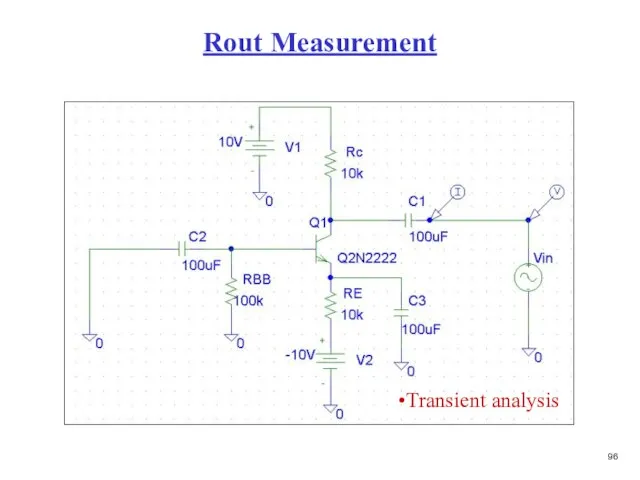
- 97. Rout Measurement Transient analysis
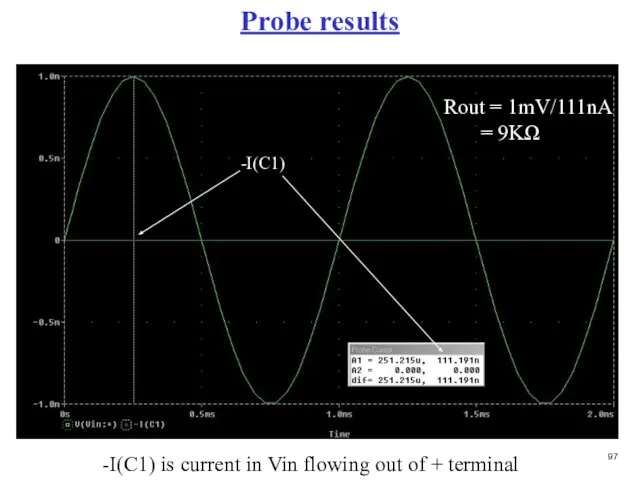
- 98. Probe results -I(C1) Rout = 1mV/111nA = 9KΩ -I(C1) is current in Vin flowing out of
- 99. DC Power measurements Power delivered by + 10 sources: (10)(872μA) + (10)(877μA) = 8.72mW + 8.77mW
- 101. Скачать презентацию






![Example -5 RBB1 = RB1||RB2 = 33K VBB1 = VCC[RB2/(RB1+RB2)] VBB1 =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/374487/slide-20.jpg)








![ac equivalent circuit b e c vbe = (Rb||Rpi)/ [(Rb||Rpi) +Rs]vi vbe](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/374487/slide-38.jpg)










![Prob. (d) find vb1/vi vb1/vi = Rin1/[RS + Rin1] = 0.82 b1](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/374487/slide-81.jpg)






 Инструменты развития туризма
Инструменты развития туризма  признака параллельности прямых 7 класс
признака параллельности прямых 7 класс Политическая карикатура как орудие неформальной коммуникации
Политическая карикатура как орудие неформальной коммуникации Москва во главе объединения русских земель
Москва во главе объединения русских земель Художник в театре
Художник в театре РАЗВИТИЕ СЕЛА
РАЗВИТИЕ СЕЛА Основы интернет-инвестиций. Биржа ММВБ и торговля на ней
Основы интернет-инвестиций. Биржа ММВБ и торговля на ней Турецкий поток
Турецкий поток Международный трибунал по морскому праву
Международный трибунал по морскому праву Квест - Моя конституция
Квест - Моя конституция New Patrol
New Patrol Химический элемент - водород
Химический элемент - водород Презентация на тему Как мы победили микробов
Презентация на тему Как мы победили микробов Постновогодний кулинарный синдром
Постновогодний кулинарный синдром Литейное производство. Опоки. (Лекция 5)
Литейное производство. Опоки. (Лекция 5) Деятельность агента
Деятельность агента Презентация на тему Игра-путешествие "Права детей"
Презентация на тему Игра-путешествие "Права детей" Киринское газоконденсатное месторождение
Киринское газоконденсатное месторождение Компьютерные программы. Урок 4
Компьютерные программы. Урок 4 Глобальные компетенции
Глобальные компетенции Курение и здоровье
Курение и здоровье  Верстак столярный
Верстак столярный Компания
Компания 909900693.180706935048242676.1.2(1)
909900693.180706935048242676.1.2(1) Презентация на тему Здравствуй, школа(День знаний в 1 классе)
Презентация на тему Здравствуй, школа(День знаний в 1 классе)  Ковбои
Ковбои Модели спецодежды для мужчин (основные рабочие)
Модели спецодежды для мужчин (основные рабочие) Практика. Один iз проектiв
Практика. Один iз проектiв