C1 метод мажорант

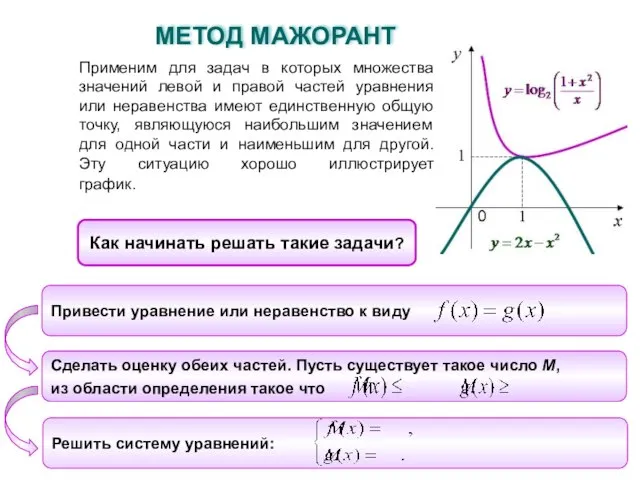
Применим для задач в которых множества значений левой и правой частей уравнения или неравенства имеют единственную общую точку, являющуюся наибольшим значением для одной части и наименьшим для другой. Эту ситуацию хорошо иллюстрирует график.
Как начинать решать такие задачи?
МЕТОД МАЖОРАНТ
Привести уравнение или неравенство к виду
Сделать оценку обеих частей. Пусть существует такое число М,
из области определения такое что

удовлетворяет второму уравнению.
Решение. Оценим обе части уравнения.
При всех значениях х верны неравенства:
Следовательно, данное уравнение равносильно системе:

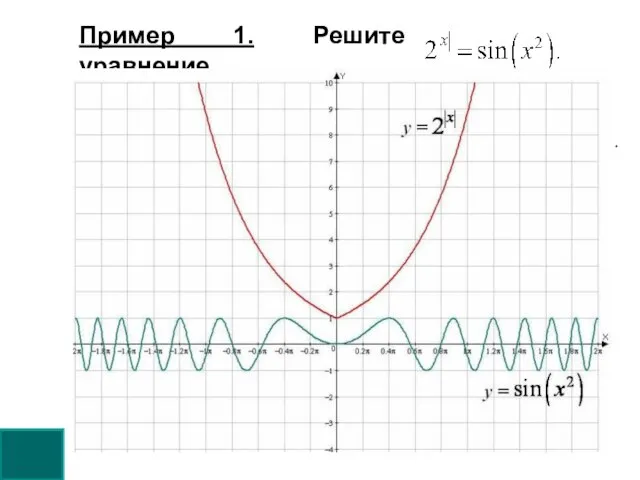
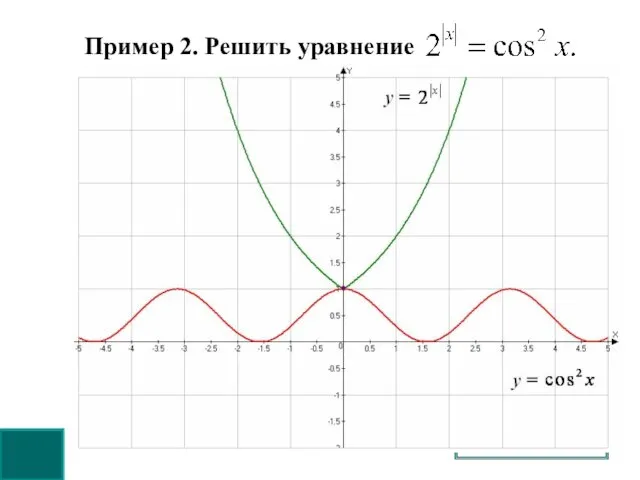
Пример 2. Решить уравнение
Решение: Оценим обе части уравнения.
Следовательно, данное уравнение равносильно системе:
При х = 0 второе уравнение обращается в тождество, значит
х = 0 корень уравнения.
Ответ: х = 0.
Графическая иллюстрация

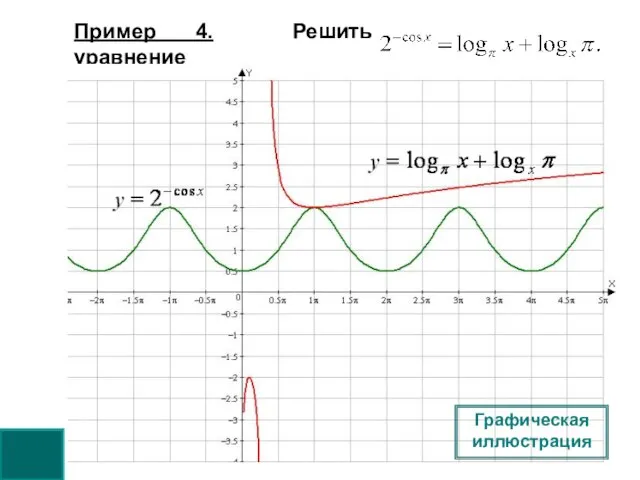
Пример 4. Решить уравнение
Для правой части (в силу неравенства для суммы двух взаимно
обратных чисел) выполнено
Поэтому уравнение имеет решения, если и только если
одновременно выполнены два условия
принимает значение от 0,5 до 2.
Решение. Оценим обе части уравнения.
Графическая иллюстрация

Пример 5. Решить уравнение
Решением первого уравнения системы являются значения
Решение. Оценим обе части уравнения.

Пример 6. Решить уравнение
в том случае, когда оба слагаемых одновременно равны 1.
Следовательно, данное уравнение равносильно системе уравнений
.
Решение.

Пример 7. Решить уравнение
Решение. Очевидно, что
почленно эти неравенства, получаем:
Следовательно, левая часть равна правой, лишь при условии:
Значит, данное уравнение равносильно системе уравнений:
Решая систему уравнений, получаем корни:
.
Заметим, что перемножив
Ответ:

Проверим справедливость первого равенства, подставив эти корни.
При
Пример 8. Решите уравнение
Решение. Для решения уравнения
оценим его части:
Поэтому равенство возможно только при условии
Сначала решим второе уравнение:
Корни этого уравнения
Итак, данное уравнение имеет единственный корень х = 0.
Ответ: 0.
При х = -1 имеем: