Содержание
- 2. 5. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 2002. – 405 с. 6.
- 3. Лекция №1 Закон больших чисел и Центральная предельная теорема
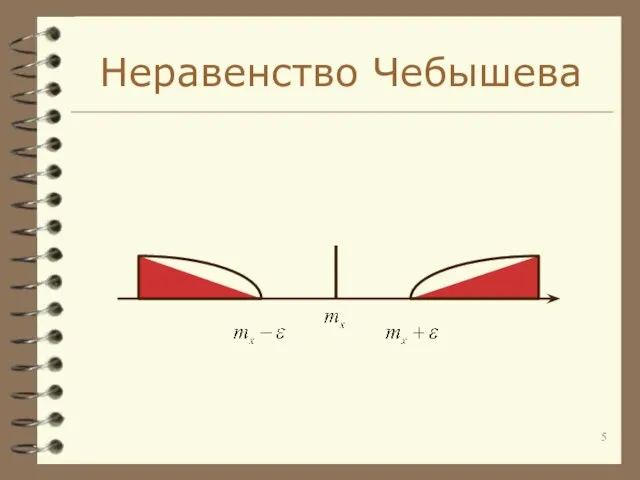
- 4. Неравенство Чебышева
- 5. Неравенство Чебышева
- 6. Сходимость по вероятности Последовательность случайных величин Сходится по вероятности к величине a если для любых ε
- 7. Сходимость по вероятности
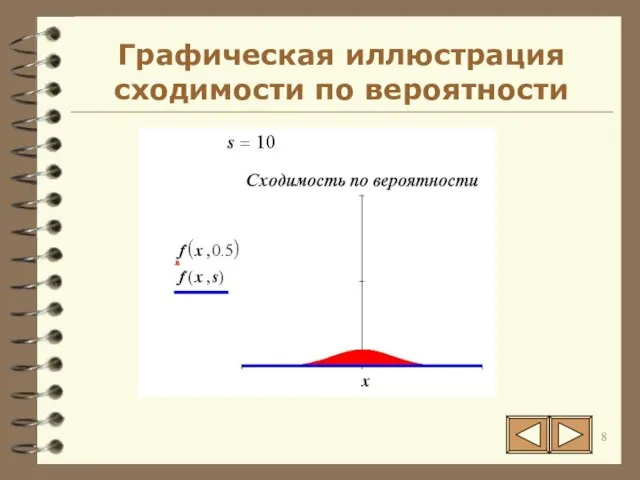
- 8. Графическая иллюстрация сходимости по вероятности
- 9. Теорема Чебышева При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющей конечную
- 10. Теорема Чебышева
- 11. Обобщенная теорема Чебышева При неограниченном увеличении числа независимых испытаний над случайными величинами, имеющими ограниченные дисперсии, среднее
- 12. Обобщенная теорема Чебышева
- 13. Теорема Бернулли При неограниченном увеличении числа независимых опытов в постоянных условиях частота рассматриваемого события А сходится
- 14. Индикатор События И Его Свойства Индикатор события – это случайная величина, принимающая значение, равное единице, если
- 15. Ряд распределения Индикатора События Математическое ожидание и дисперсия индикатора
- 16. Теорема Пуассона При неограниченном увеличении числа независимых испытаний в переменных условиях частота события сходится по вероятности
- 17. Центральная Предельная Теорема Рассматривается вопрос о законе распределения суммы случайных величин, когда число слагаемых неограниченно возрастает
- 18. Теорема Ляпунова Если случайные величины взаимно независимы и имеют один и тот же закон распределения с
- 20. Скачать презентацию















 Сознание vs личная эффективность
Сознание vs личная эффективность Презентация на тему Кирилл и Мефодий
Презентация на тему Кирилл и Мефодий Методическая система оценки достижений метапредметных результатов как критерия качества образования
Методическая система оценки достижений метапредметных результатов как критерия качества образования 10 Cars to Consider as Your First Buy
10 Cars to Consider as Your First Buy Презентация на тему Второй закон термодинамики
Презентация на тему Второй закон термодинамики Лес и его обитатели
Лес и его обитатели Защита от несанкционированного доступа к информации
Защита от несанкционированного доступа к информации Первая помощь при растяжении связок, вывихах суставов, переломах костей
Первая помощь при растяжении связок, вывихах суставов, переломах костей Добро пожаловать в Pelcom
Добро пожаловать в Pelcom Попутешествуем вместе… Крепости Ленинградской области
Попутешествуем вместе… Крепости Ленинградской области Презентация на тему Ручные работы (5 класс)
Презентация на тему Ручные работы (5 класс) Тест для родителей:
Тест для родителей: Презентация на тему Экономика: наука и хозяйство
Презентация на тему Экономика: наука и хозяйство Строительство железной дороги
Строительство железной дороги Работу подготовил учащийся 13 группы Авакумов Денис
Работу подготовил учащийся 13 группы Авакумов Денис Рисуем в технике примакивание
Рисуем в технике примакивание 20161212_prezen.giokruiz
20161212_prezen.giokruiz Ансамбль. Чёрный тюльпан
Ансамбль. Чёрный тюльпан Свойства древесины
Свойства древесины Перемещение и копирование файлов и папок
Перемещение и копирование файлов и папок ПОДВЕДЕНИЕ ИТОГОВ
ПОДВЕДЕНИЕ ИТОГОВ Чему я научилась на курсе коммуникативной медиа-журналистики
Чему я научилась на курсе коммуникативной медиа-журналистики Теоретические основы
Теоретические основы Праздничный девичий костюм мордвы-эрзя
Праздничный девичий костюм мордвы-эрзя Презентация на тему Русская игрушка - Матрешка
Презентация на тему Русская игрушка - Матрешка Arvo-Tec RAS проект
Arvo-Tec RAS проект Кормление котят
Кормление котят История развития рекламы в России Соколова Анастасия РГГУ / ФУ / 5 курс / гр.№7
История развития рекламы в России Соколова Анастасия РГГУ / ФУ / 5 курс / гр.№7