Содержание
- 2. Решить устно уравнения а) x2 = 0 ж) x3 – 25x = 0 б) 3x –
- 3. Целое уравнение и его корни Тема урока
- 4. Основная цель урока: Обобщить и систематизировать знания о целых уравнениях и методах их решений.
- 5. Целые уравнения Уравнения, в которых левая и правая часть являются целыми выражениями называются целыми уравнениями. Степенью
- 6. Какова степень знакомых нам уравнений? а) x2 = 0 ж) x3 – 25x = 0 б)
- 7. Целые уравнения В учебнике найдите № 205. Посмотрите на уравнения а), б) и в). Чем они
- 8. Целые уравнения Решите уравнения: 2∙х + 5 =15 0∙х = 7 Сколько корней может иметь уравнение
- 9. Целые уравнения Решите уравнения: I вариант II вариант III вариант x2-5x+6=0 y2-4y+7=0 x2-12x+36=0 D=1, D>0, D=-12,
- 10. Целые уравнения Решите уравнения: I вариант II вариант III вариант x3-1=0 x3- 4x=0 x3-12x2+36x=0 x3=1 x(x2-
- 11. Целые уравнения Как вы думаете сколько корней может иметь уравнение IV, V , VI, VII, n-й
- 12. Целые уравнения Мы с вами сегодня решали уравнения аналитическим способом, но существует не только этот способ.
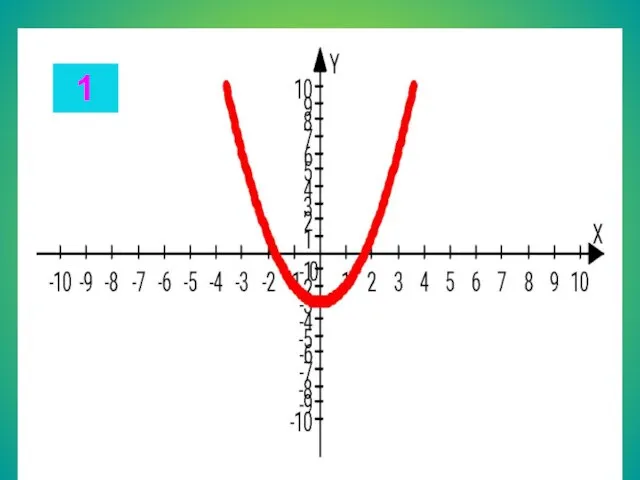
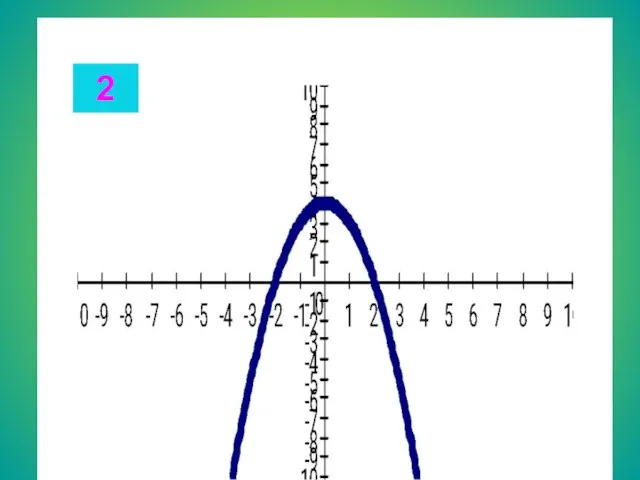
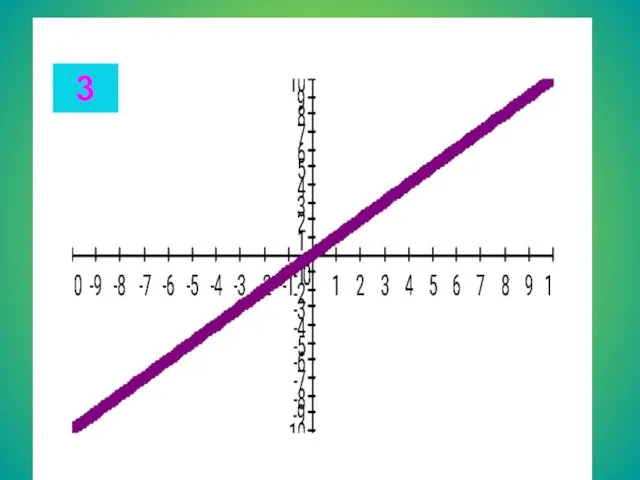
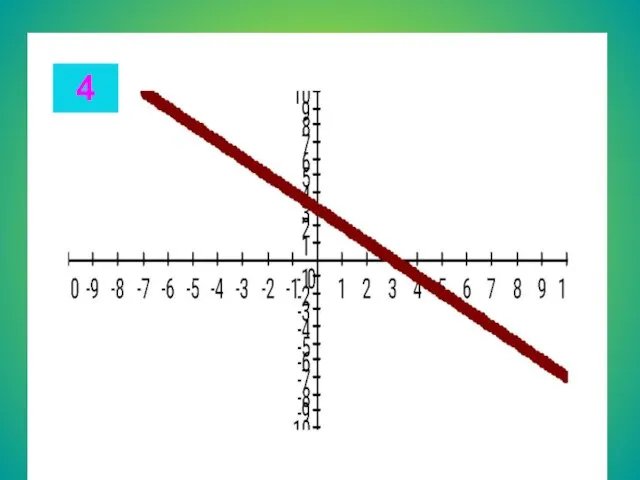
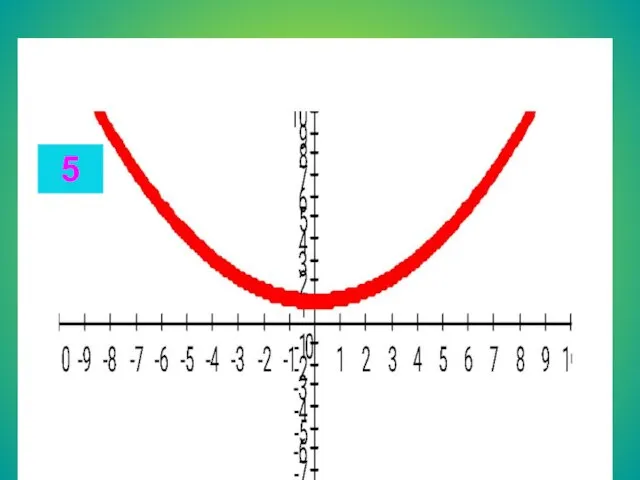
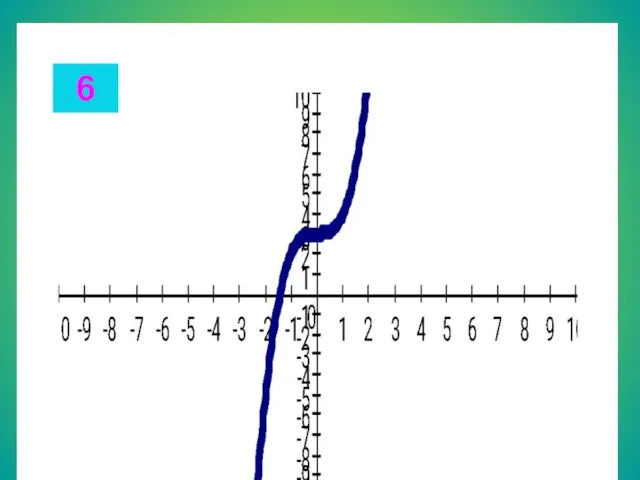
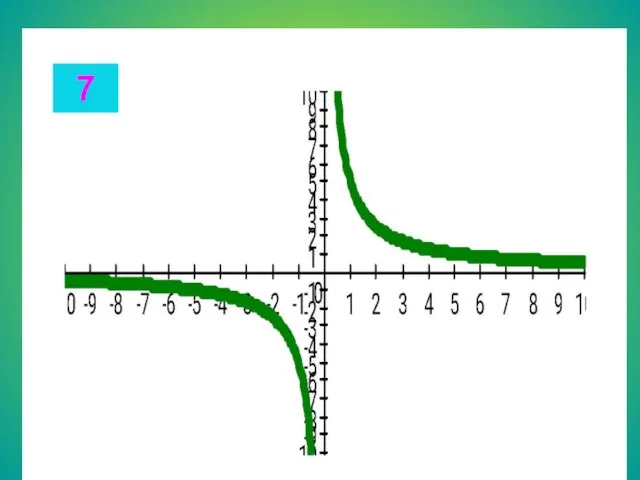
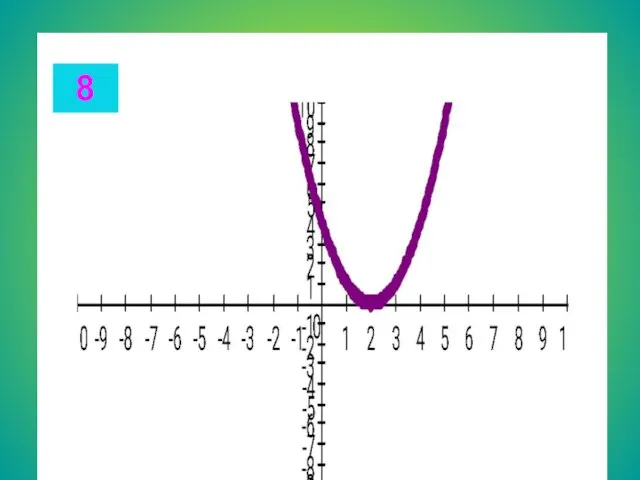
- 13. Целые уравнения Из списка функций приведенного на доске выберите функцию, соответствующую данному графику. Запишите в тетради
- 14. 1
- 15. 2
- 16. 3
- 17. 4
- 18. 5
- 19. 6
- 20. 7
- 21. 8
- 22. 1 2 3 4 5 6 7 Проверьте правильность выполнения задания своего соседа по парте 8
- 23. Целые уравнения А сейчас рассмотрим еще один (графический) способ решение уравнения I I I степени? Уравнение
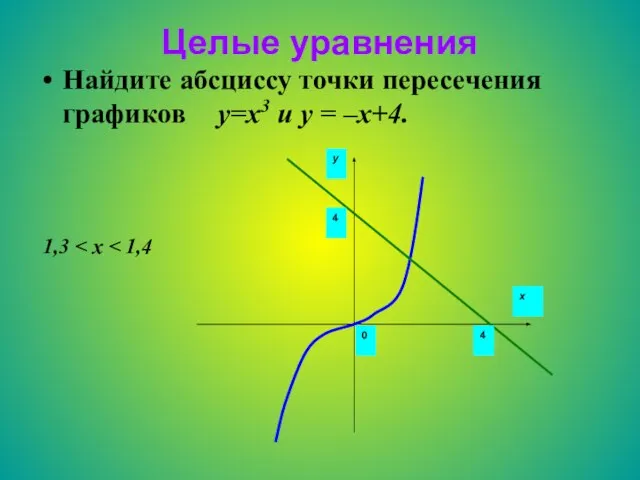
- 24. Целые уравнения Найдите абсциссу точки пересечения графиков y=x3 и y = –x+4. 1,3
- 25. Попробуйте назвать корень данного уравнения! Как вы думаете, в чём недостаток данного метода решения? Да, графический
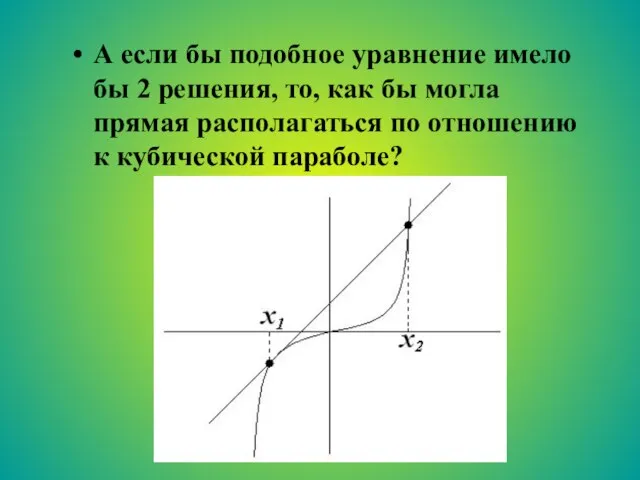
- 26. А если бы подобное уравнение имело бы 2 решения, то, как бы могла прямая располагаться по
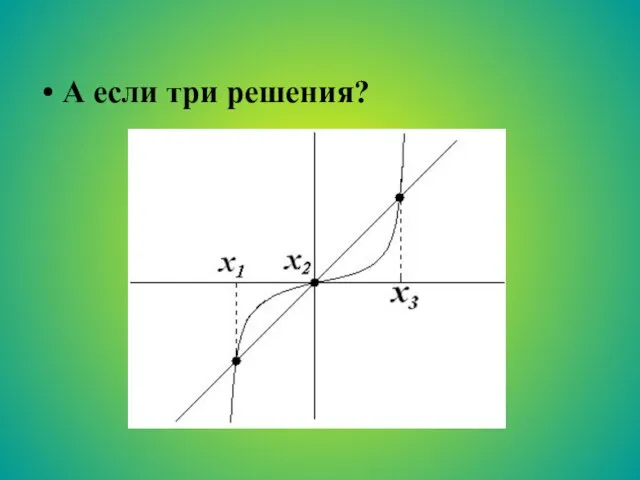
- 27. А если три решения?
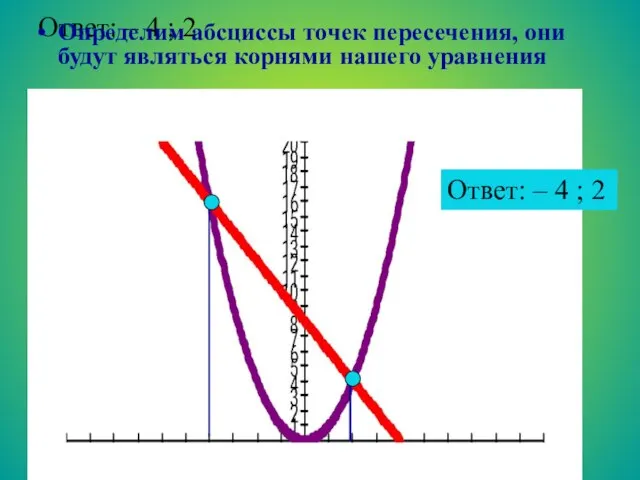
- 28. Рассмотрите пример решения уравнения графическим способом Чтобы решить уравнение х2 + 2х – 8 =0 представим
- 29. Ответ: – 4 ; 2 Определим абсциссы точек пересечения, они будут являться корнями нашего уравнения Ответ:
- 30. Ответ: -3; 2 Ответ: 1 Ответ: 2 А теперь попробуем все теоретические знания применить на практике.
- 32. Скачать презентацию
















 Примерный эскиз баннера. Kronomir
Примерный эскиз баннера. Kronomir Глава 3. Экономика фирмы
Глава 3. Экономика фирмы Гончарова Ирина Алексеевна
Гончарова Ирина Алексеевна Оценка стоимости бренда
Оценка стоимости бренда Латинская Америка
Латинская Америка Психологическая служба школы«Ни себя, нм других нельзя изучать иначе как в деятельности и общении. Нельзя изучать человека холод
Психологическая служба школы«Ни себя, нм других нельзя изучать иначе как в деятельности и общении. Нельзя изучать человека холод Необычные факты о птицах
Необычные факты о птицах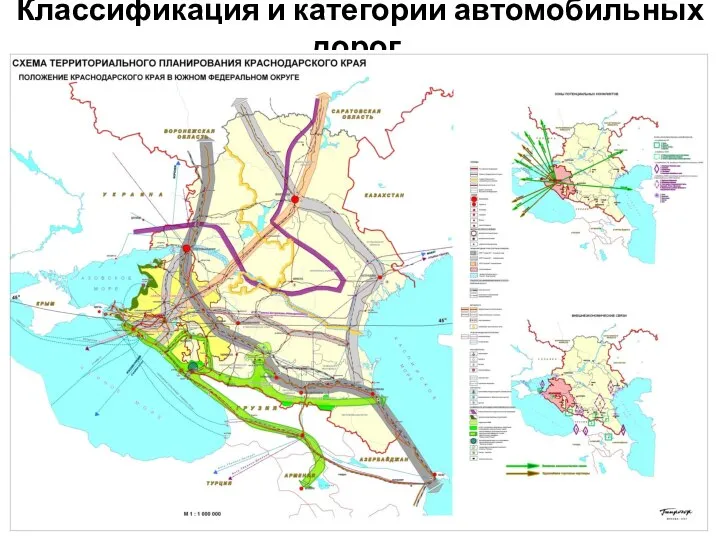 Классификация и категории автомобильных дорог
Классификация и категории автомобильных дорог Этикет 4 класс
Этикет 4 класс Влияние вредных привычек на сердечно-сосудистую и дыхательную системы
Влияние вредных привычек на сердечно-сосудистую и дыхательную системы Воля. Виды и содержания волевых процессов
Воля. Виды и содержания волевых процессов Э-74 Против курения
Э-74 Против курения Агентство по ипотечному жилищному кредитованию
Агентство по ипотечному жилищному кредитованию Возрождение Руси. Иван Калита
Возрождение Руси. Иван Калита Растительные сообщества и взаимосвязи в них
Растительные сообщества и взаимосвязи в них Чтение слов и предложений с буквой Ц
Чтение слов и предложений с буквой Ц Презентация на тему Древние германцы и Римская империя
Презентация на тему Древние германцы и Римская империя  Системный анализ предметной области кандидатской диссертации
Системный анализ предметной области кандидатской диссертации School subjects
School subjects Архимедова сила (7 класс)
Архимедова сила (7 класс) Здравствуй, милая картошка!
Здравствуй, милая картошка! Три среды обитания. Наземно-воздушная среда
Три среды обитания. Наземно-воздушная среда Формованный эластичный ППУ для автомобильной промышленности
Формованный эластичный ППУ для автомобильной промышленности Расшифровка моделей Indesit
Расшифровка моделей Indesit Выполнение эскиза в точечной технике
Выполнение эскиза в точечной технике Особенности питания студентов
Особенности питания студентов Портфолио педагога
Портфолио педагога Воспитательные традиции в системе дополнительного образования
Воспитательные традиции в системе дополнительного образования