симметрия. В математике (точнее, евклидовой геометрии) осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две — в плоскости фигуры), если это не квадрат.
Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию (другие термины — радиальная, аксиальная, лучевая симметрии) относительно поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но конус будет.
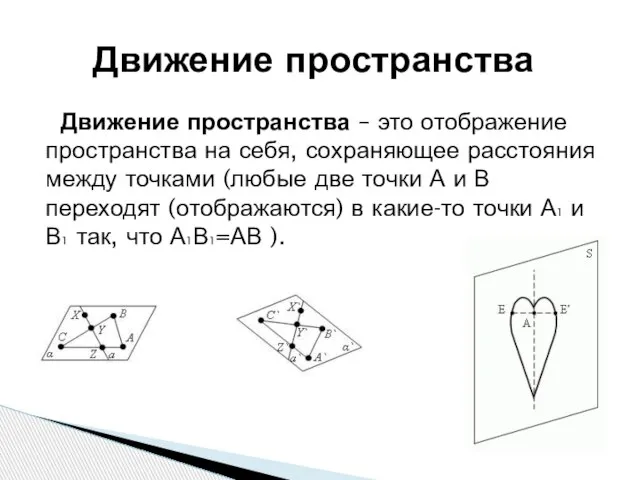
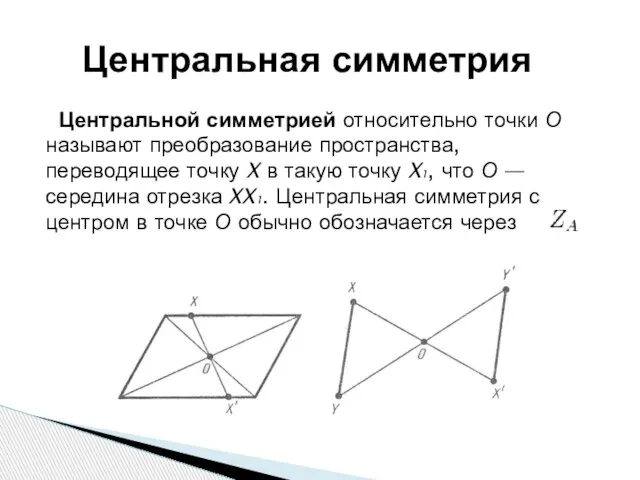
Осевая симметрия



 Новый подход к решению систем уравнений в задачах дискретного логарифмирования
Новый подход к решению систем уравнений в задачах дискретного логарифмирования Топологии компьютерных сетей
Топологии компьютерных сетей Usability интернет-магазина: как сделать сайт удобным и «продающим» Боровский Александр, специалист по онлайн-продвижению. ЛІГАБізн
Usability интернет-магазина: как сделать сайт удобным и «продающим» Боровский Александр, специалист по онлайн-продвижению. ЛІГАБізн Усадьба Поленово
Усадьба Поленово Разнообразие природы
Разнообразие природы Климат России
Климат России Презентация на тему Здоровый образ жизни (5 класс)
Презентация на тему Здоровый образ жизни (5 класс) Презентация на тему В мире камня (2 класс)
Презентация на тему В мире камня (2 класс) Берлинская наступательная операция
Берлинская наступательная операция МТО ПЗ 1
МТО ПЗ 1 Виды проектов
Виды проектов Урок русского языка
Урок русского языка Государство и культура: определения, взаимное влияние, политическая культура
Государство и культура: определения, взаимное влияние, политическая культура НАШИ ВЫПУСКНИКИ(1989/2009)
НАШИ ВЫПУСКНИКИ(1989/2009)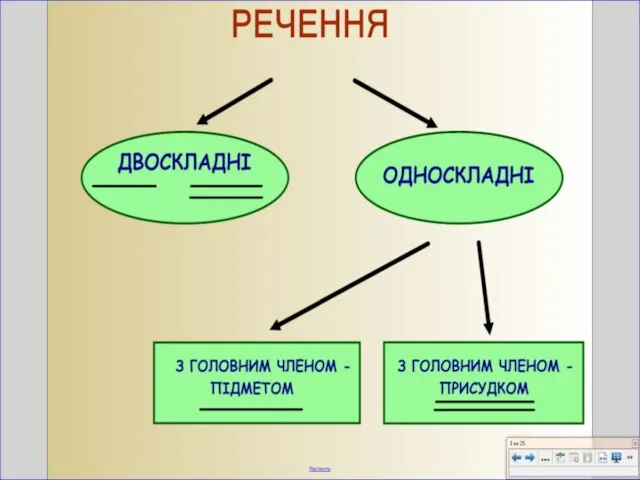 Називні речення
Називні речення Презентация на тему Равновесие тел урок физики, 10 класс
Презентация на тему Равновесие тел урок физики, 10 класс  Оренгбурский пуховой платок
Оренгбурский пуховой платок Правоохранительные органы
Правоохранительные органы Масленица 2021 в Светлицах
Масленица 2021 в Светлицах Организационная культура. Понятие, структура, функции
Организационная культура. Понятие, структура, функции День Святителя Николая Чудотворца
День Святителя Николая Чудотворца Рекламное агентство "Здоровье"
Рекламное агентство "Здоровье" Презентация на тему Горы России
Презентация на тему Горы России Presentation (2)
Presentation (2) Подлежащее
Подлежащее Презентация на тему Русский язык - богатство России
Презентация на тему Русский язык - богатство России ОБ ИЗМЕНЕНИЯХ В СОЦИАЛЬНОЙ СФЕРЕ, СВЯЗАННЫХ С РЕАЛИЗАЦИЕЙ ЗАКОНА РОССИЙСКОЙ ФЕДЕРАЦИИ ОТ 08.05.2010 № 83-ФЗ «О ВНЕСЕНИИ ИЗМЕНЕНИЙ В ОТД
ОБ ИЗМЕНЕНИЯХ В СОЦИАЛЬНОЙ СФЕРЕ, СВЯЗАННЫХ С РЕАЛИЗАЦИЕЙ ЗАКОНА РОССИЙСКОЙ ФЕДЕРАЦИИ ОТ 08.05.2010 № 83-ФЗ «О ВНЕСЕНИИ ИЗМЕНЕНИЙ В ОТД Наплавка валиков в вертикальном положении сварочного шва
Наплавка валиков в вертикальном положении сварочного шва