Метод координат в пространстве (11 класс)

Цели урока:
1.Повторить понятия вектора;
2.Ввести понятие прямоугольной системы координат в пространстве.
Задачи урока: выработать умения строить точку по заданным её координатам и находить координаты точки, изображённой в заданной системе координат.

Содержание урока:
Повторение понятия вектора;
Прямоугольная система координат;
Понятия координат векторов;
Решение задач координатным методом;
Домашнее задание.

Как и в плоскости, в пространстве вектор определяется как направленный отрезок:
A
B
Точка А – начало вектора, В – конец вектора. Записывают: или .
a
Вектор, у которого начало совпадает с конечной точкой называется нулевым, обозначается: или .
Длина отрезка, изображающего вектор, называется модулем вектора, т.е.
Определение вектора.

Если через точку пространства
проведены три попарно перпендикулярные прямые, на каждой из них
выбрано направление и выбрана единица
измерения отрезков, то говорят, что
задана система координат в пространстве.

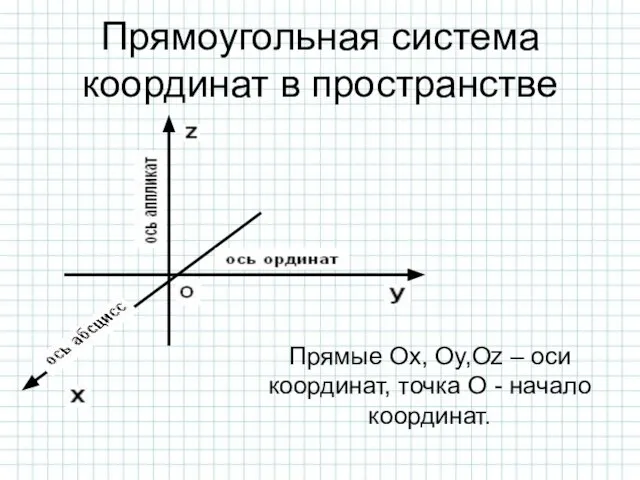
Прямоугольная система координат в пространстве
Прямые Ox, Oy,Oz – оси координат, точка О - начало координат.

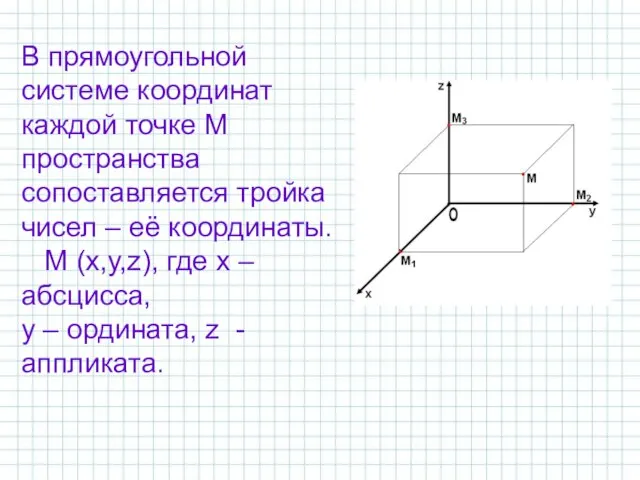
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел – её координаты.
М (х,у,z), где х – абсцисса,
у – ордината, z - аппликата.

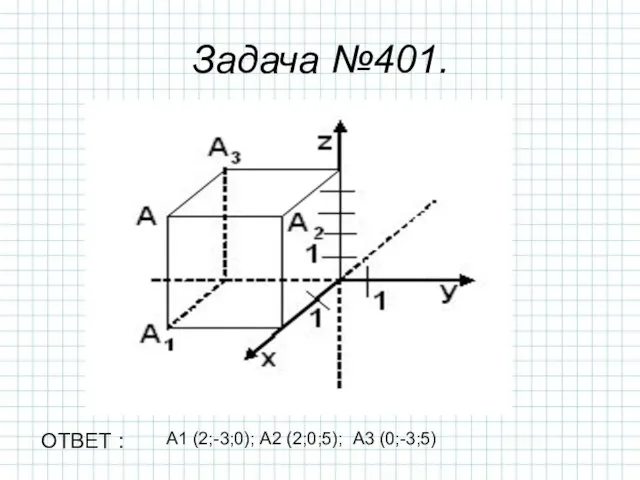
А1 (2;-3;0); А2 (2;0;5); А3 (0;-3;5)
Задача №401.
ОТВЕТ :

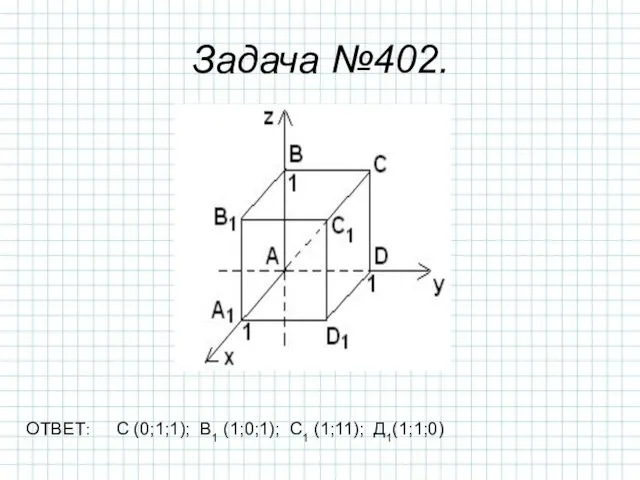
Задача №402.
ОТВЕТ:
С (0;1;1); В1 (1;0;1); С1 (1;11); Д1(1;1;0)

Домашнее задание.
Выучить §42.
№400 д); е), № 403, №407 е),ж), з).

Координаты вектора
Цель урока:
Изучить метод координат.

План урока:
Дать понятие единичных векторов;
Рассмотреть правила сложения, вычитания, умножения;
Решение задач;
Домашняя работа.

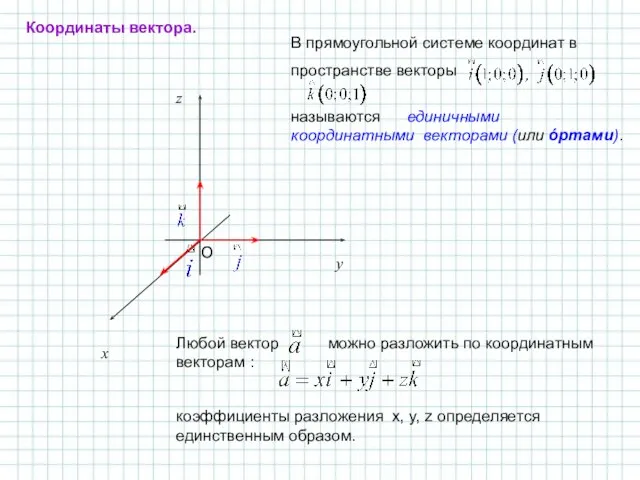
В прямоугольной системе координат в
пространстве векторы
называются единичными координатными векторами (или óртами).
x
z
O
Любой вектор можно разложить по координатным векторам :
коэффициенты разложения x, y, z определяется единственным образом.
y
Координаты вектора.

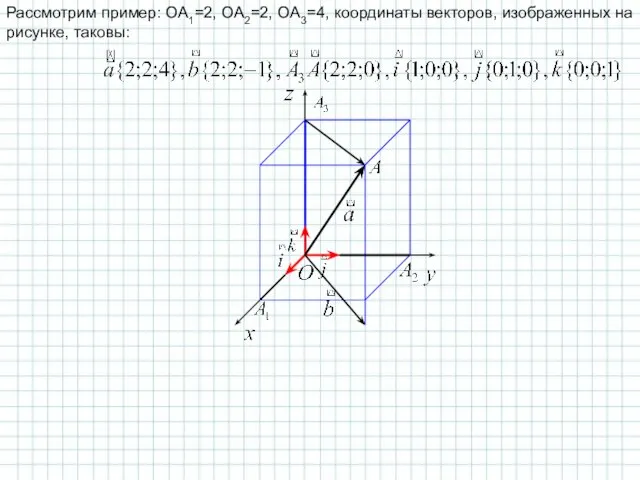
Рассмотрим пример: OA1=2, OA2=2, OA3=4, координаты векторов, изображенных на рисунке, таковы:

10. Каждая координата суммы 2х или более векторов равна сумме соответствующих координат этих векторов, т.е.
20. Каждая координата разности 2х векторов равна разности соответствующих координат этих векторов, т.е.
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Задача
Даны векторы:
Найти координаты векторов:
Решение:
1.
2. И
3.
Ответ:

Самостоятельная работа
Вариант 1
Найти координаты векторов:
Вариант 2
Найти координаты векторов:
Даны векторы: