Численное интегрирование

Если функция f(x)
непрерывна на отрезке
то определенный интеграл
от этой функции в пределах от a до b
существует и имеет вид

Найти определенный интеграл
на отрезке
если подынтегральная функция
на отрезке задана таблично.
Формулы
приближенного интегрирования
называются
квадратурными формулами.
Задача численного
интегрирования

Метод прямоугольников
основан на непосредственном
определении интеграла:
где
- интегральная сумма, соответствующая некоторому разбиению отрезка
и некоторому выбору точек
,
,…,
на отрезках разбиения

Вычисление определенного
интеграла
геометрически сводится
к вычислению площади
криволинейной трапеции,
ограниченной функцией f(x),
осью абсцисс и прямыми x = a и x = b.

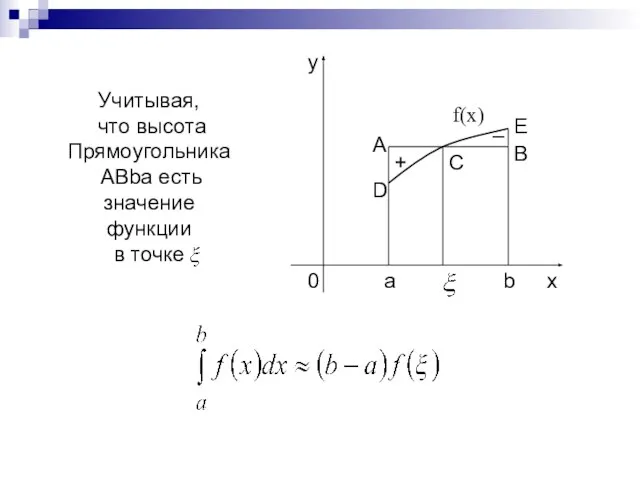
Учитывая,
что высота
Прямоугольника
ABba есть
значение
функции
в точке
f(x)
–

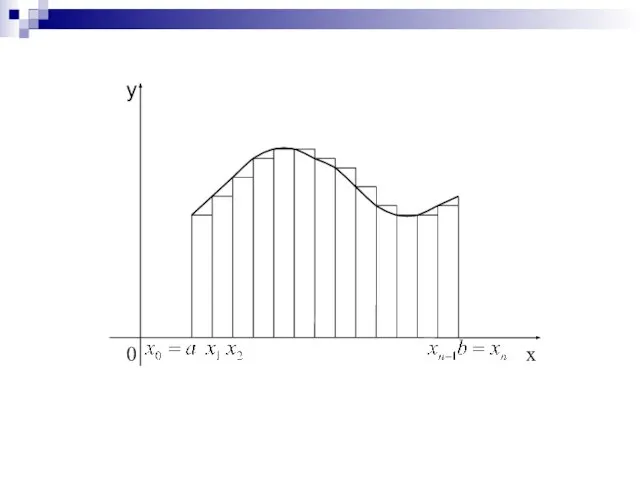
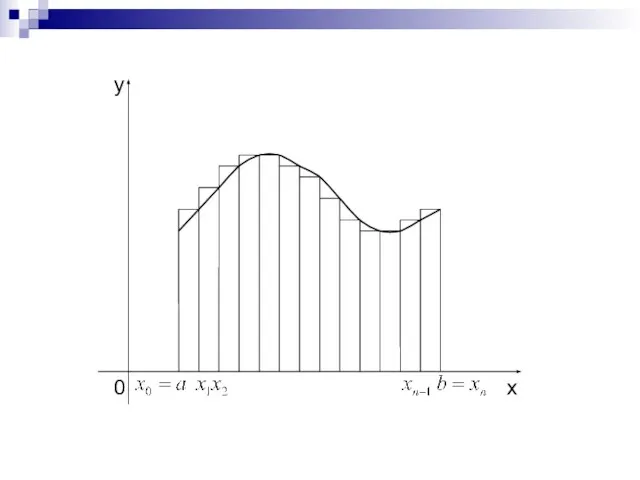
Для увеличения точности
численного интегрирования
можно отрезок
разбить на несколько частей и для каждой из них вычислить
приближенное значение
площади криволинейной
трапеции, основанием которой
является отрезок
(i = 0, 1, …,n – 1),
а высотой число
т.е. значение функции
в точке

Практически удобно делить
отрезок
на равные части, а точки
(i = 0, 1, …, n – 1) совмещать с левыми
или с правыми
концами отрезков разбиения.

Если точку
совместить с левым концом
отрезка
то приближенное значение
интеграла может быть
представлено
формулой левых
прямоугольников:
где
– шаг.

Если же в качестве точки
выбрать правый конец отрезка
то приближенное значение
интеграла вычисляется
по формуле правых
прямоугольников:
.

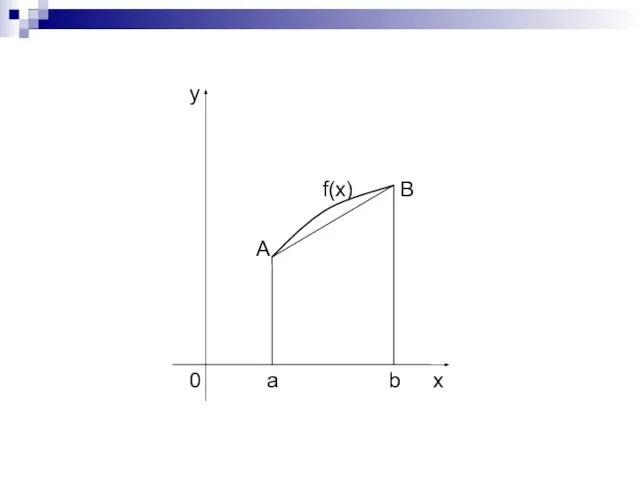
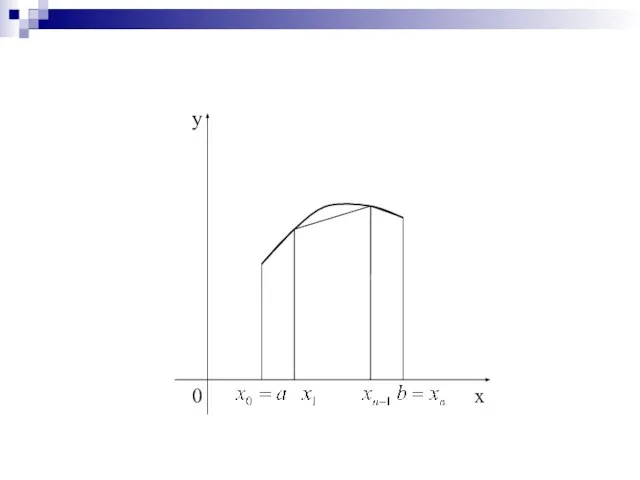
Метод трапеций
Заменим на отрезке
дугу AB графика
подынтегральной функции y = f(x)
стягивающей ее хордой и
вычислим площадь трапеции ABba.
Примем значение определенного
интеграла численно равным
площади этой трапеции:
Это и есть формула трапеций

Если отрезок
разделить на несколько
частей и применить
формулу трапеции
к каждому отрезку
Тогда

Для простоты вычислений
удобно разделить отрезок
на равные части,
в этом случае длина
каждого из отрезков
разбиения есть
Численное значение
интеграла на отрезке
равно

А на всем отрезке
соответственно
Эта формула называется
общей формулой трапеции.
Ее можно переписать в виде
где
– шаг.

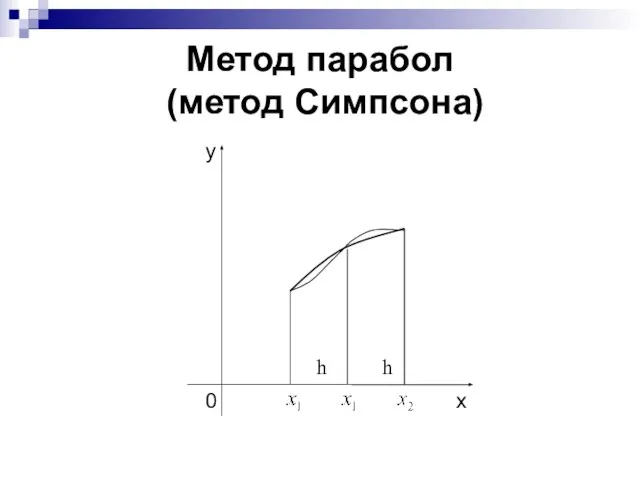
Метод парабол
(метод Симпсона)
h
h

функцию y = f(x) на отрезке
заменяем квадратичной функцией,
принимающей в узлах
,
,
значения
,
и
В качестве интерполяционного
многочлена воспользуемся
многочленом Ньютона

Тогда
Это соотношение
называется формулой Симпсона.

Для увеличения точности
вычислений отрезок
разбивают на n пар участков и заменяя подынтегральную
функцию интерполяционным
многочленом Ньютона
второй степени, получают
приближенное значение
интеграла на каждом участке
длины 2h:

……………………………………