Circular Motion

Circular motion
We can now extend the ideas of Newton’s Laws and the conservation of energy to motion in a circle.
First, define ω(t) = dθ/dt as the angular velocity.

Circular Motion Vectors
Circular Motion Vectors
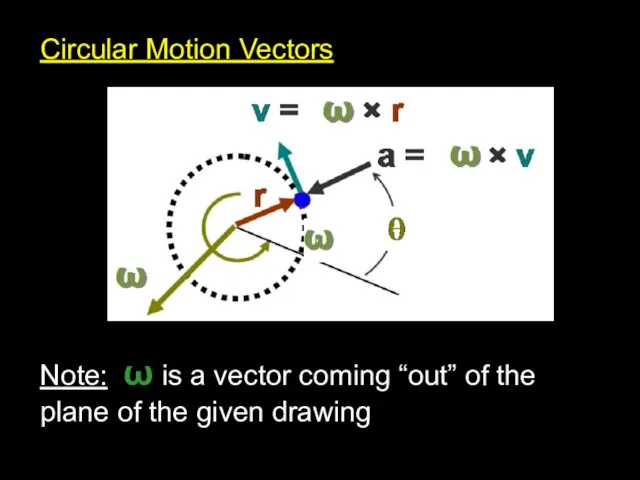
Note: ω is a vector coming “out” of the plane of the given drawing

Summary

Centripetal force
Clearly, if an object is accelerating there must be a force acting on it. The force which causes centripetal acceleration is called the centripetal force.

Centripetal force

Example 1
A tube is been placed upon the table and shaped into a three-quarters circle. A golf ball is pushed into the tube at one end at high speed. The ball rolls through the tube and exits at the opposite end. Describe the path of the golf ball as it exits the tube.
Why does the golf ball
act in that it way?

An LP rotating at 33.3 rpm

Example 2
A 5 tenge coin is placed at the edge of a record, i.e., an old fashioned LP, of diameter d = 30 cm. The record makes 33.3 revolutions per minute.
a) draw a free body diagram of the forces acting on the coin
b) find the angular speed of the record
c) if the coin is 2 g and the maximum frictional force provided by the LP is 6.0 x 10-4 N, calculate whether the coin will stay on or slip off.

Circular motion for non-constant ω
For objects moving in a circle, the angular speed, ω, will generally not be constant.
For example: a stone at the end of a string moving in a vertical circle, or a skateboarder in a hemispherical ‘bowl’, an airplane looping the loop!
This is because the centripetal force is varying.

Example 3
A stone at the end of a piece of string moves vertically with a circular motion about O. Its mass is 0.15 kg, speed at the top is 3.5 m s-1 and the string is 0.7 m.
a) Sketch a free body diagram for the stone at the top of the circle
b) Find the resultant force on the stone at that position
c) Find the tension in the string at that position
d) Calculate T when the stone is at the bottom of the circle
(take g = 9.81 m s-2)