Cours d’infographie rappels

Rappels de géométrie
Transformations 2D
Transformations 3D
Rappels d’Algèbre
Plan

Rappels de géométrie
Transformations 2D

C’est l’ensemble des transformations du plan pouvant être appliquées aux pixels de l’image, sans considération de l’intensité.
Transformation 2D

Représenter les changements d’espaces de coordonnées et manipuler les points dans l’espace et dans l’image
Transformation 2D

Par exemple
Réduction, agrandissement
Déformation d’images
Transformation 2D

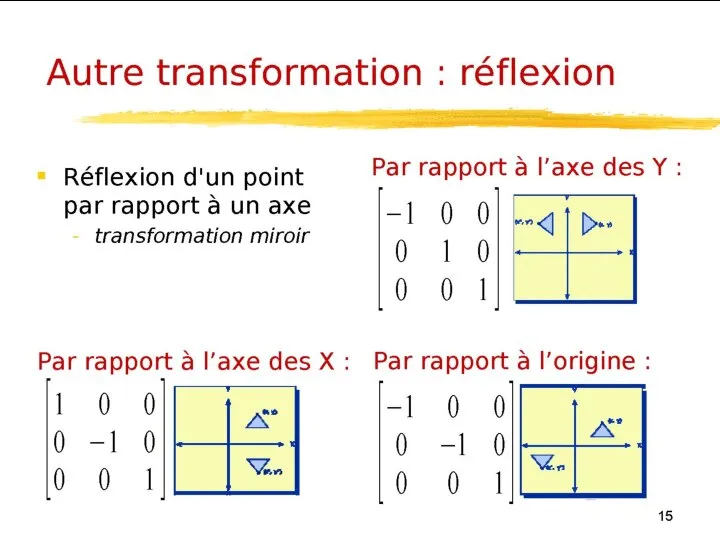
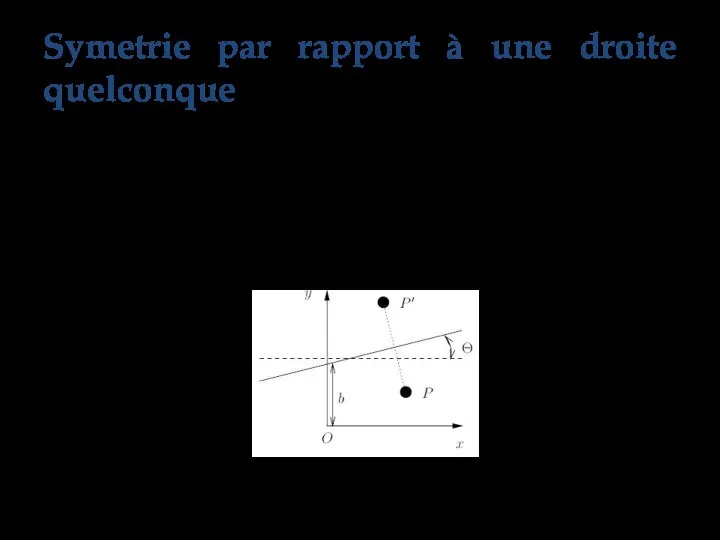
Le calcul du symètrie d’un point P par rapport à une droite d’équation y=ax+b est effectué en appliquant les transformations élémentaires suivantes :
Symetrie par rapport à une droite quelconque

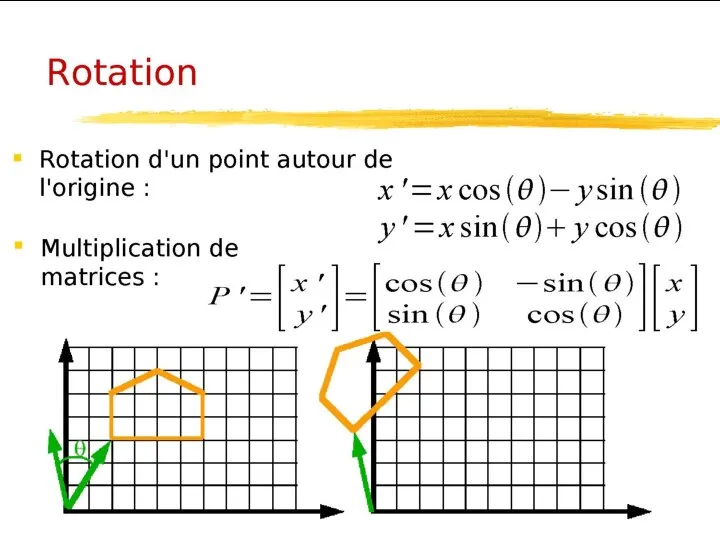
Translation (0, -b) (on fait passer la droite par l’origine );
Rotation d’angle -Ө, où Ө = atan(a);
Symétrie par rapport à l’axe Ox;
Rotation d’angle Ө;
Translation de vecteur (0, b).
Symetrie par rapport à une droite quelconque

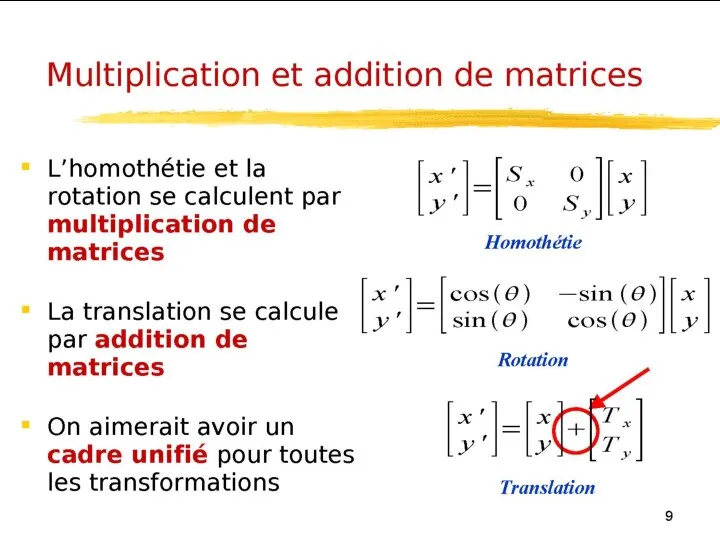
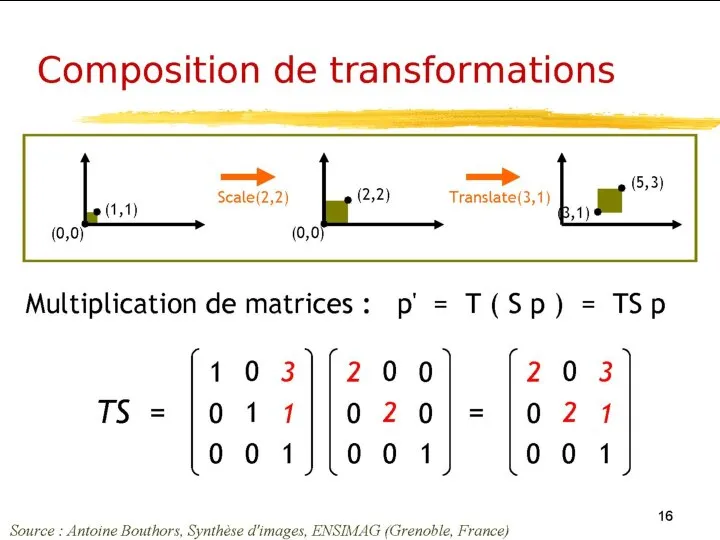
Une image plane est une collection de points (x1,y1), (x2,y2), ... , (xn,yn).
Pour appliquer une transformation à l'image il suffit d'appliquer cette transformation à chacun des points.
Ces calculs peuvent être fait d'un seul coup en rangeant les points dans une matrice :
Représentation des objets

et en multipliant cette matrice par la matrice M de la transformation :
Représentation des objets

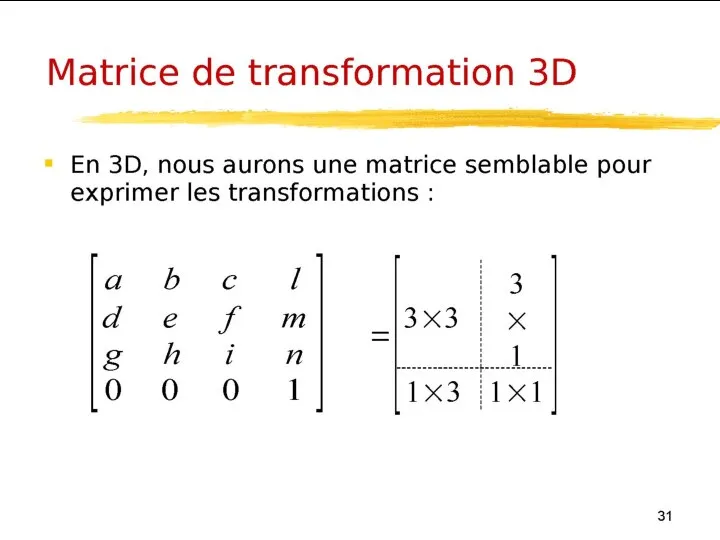
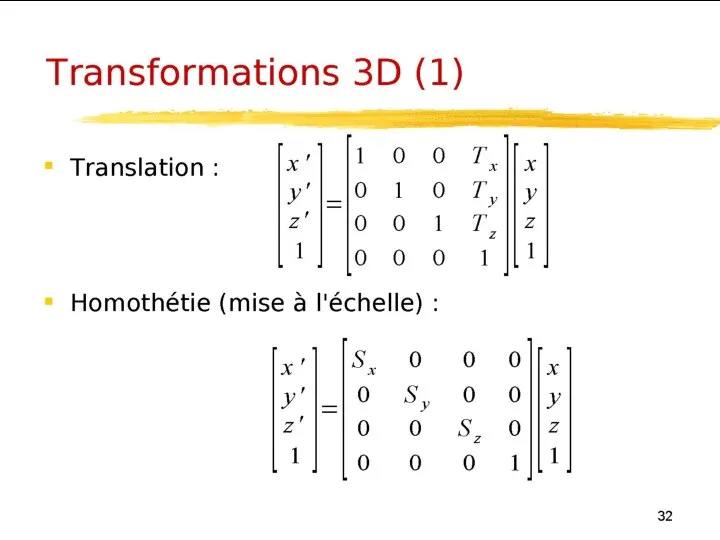
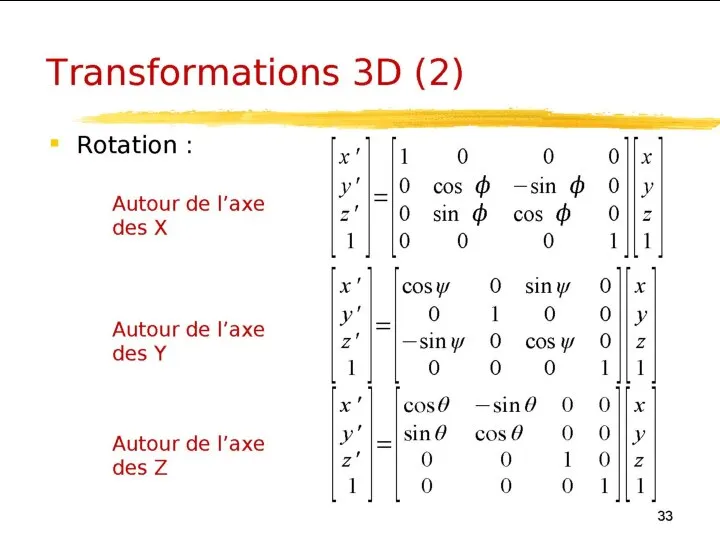
Rappels de géométrie
Transformations 3D

Rappels d’Algèbre

Définition
Le produit croisé ou produit en croix de deux vecteurs du plan est défini par:
Produit en Croix (en dimension 2)

Propriétés
anti-commutatif :
associatif avec le produit d'un réel et d'un vecteur :
distributif par rapport à l'addition des vecteurs :
Produit en Croix (en dimension 2)

Interprétation
Le produit croisé fournit, un test de colinéarité pour deux vecteurs non nuls, et d'autre part, un test de placement d'un point relativement à une droite.
le produit en croix permet de retrouver l'équation d’une droite D contenant un point M, et de vecteur directeur .
Produit en Croix (en dimension 2)

On a en effet :
Produit en Croix (en dimension 2)

Définition
Le produit scalaire de deux vecteurs de l'espace (ou du plan, en oubliant la composante z), est défini par :
Produit scalaire (en dimension 2 ou 3)

Propriétés
commutatif
associatif avec le produit d'un réel et d'un vecteur : distributif par rapport à l'addition des vecteurs :
Produit scalaire (en dimension 2 ou 3)

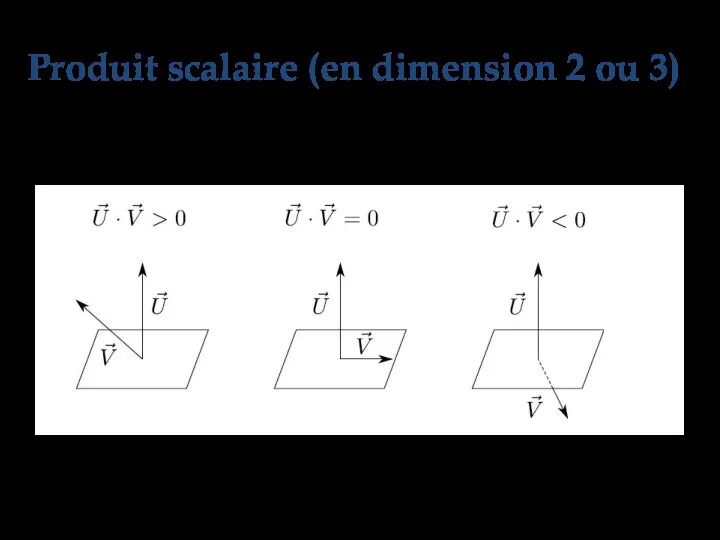
Interprétation
Le produit scalaire permet de déterminer la forme (aigu, droit, ou obtus) de l'angle entre deux vecteurs non nuls.
En 3D, il fournit également un test de placement d'un point relativement à un plan.
Produit scalaire (en dimension 2 ou 3)

Interprétation
Produit scalaire (en dimension 2 ou 3)

Interprétation
Soit à présent un plan contenant un point M, et de normale N (i.e. N est un vecteur orthogonal au plan). On a :
Produit scalaire (en dimension 2 ou 3)

Produit scalaire (en dimension 2 ou 3)

Définition
Le produit vectoriel de deux vecteurs de l'espace est défini par :
Produit vectoriel (en dimension 3)

Produit vectoriel (en dimension 3)

Propriétés
anti-commutatif :
associatif avec le produit d'un réel et d'un vecteur :
distributif par rapport à l'addition des vecteurs :
non associatif.
Produit vectoriel (en dimension 3)

Interprétation
En dimension 3, le produit vectoriel de deux vecteurs non nuls et non colinéaires produit un nouveau vecteur non nul, et orthogonal aux deux premiers
(si U ou V est nul, ou si U ;V sont colinéaires, leur produit vectoriel est le vecteur nul).
Il permet en particulier de calculer une normale N au plan engendré par un point M et deux vecteurs U et V
Produit vectoriel (en dimension 3)