Cryogenics & Cryomodules. Part 1: Catching Cold

Goal
The goal of this tutorial is to provide a background in cryogenics suitable for workers in the field of Superconducting RF along with pointers for further study
At the end of today, you should understand the basics of cryogenics and cryomodules as they apply to SRF systems
The tutorial is divided into 2 logical parts: one on making things cold i.e. refrigeration systems & He II (Catching Cold) and 1 on maintaining things cold i.e. Cryostats and cryomodules (Keeping Cold)

Outline
Part 1: Catching Cold
Introduction To Cryogenics
Basic refrigeration processes
Isenthalpic (Joule-Thomson)
Isentropic expansion
Carnot Cycle, COP and FOM
Collins Cycle and Modern Refrigeration Plants
He II (Superfluid Helium)
Definition and use in SRF systems
Two-Fluid Model
Heat Transfer
Fluid mechanics
Second Sound
He II Refrigeration Systems

Outline
Part 2: Keeping Cold
Cryogenic Safety
Oxygen Deficiency Hazards
Pressure safety
High Level Guidelines
Cryostats and Cryomodules
Definitions
Materials
Thermal Insulation Systems
Conduction
Convection
Radiation
Cryomodule Examples

What is Cryogenics ?
Cryogenics is the science & engineering of phenomena that occur at temperatures below 120 K
Cryogenic applications include:
Air Separation
MRI Systems
Cooling of superconducting magnets for research: HEP, Fusion, High Field Labs
Liquefaction of gases allows transport at high densities and low pressure: LNG, oxygen, nitrogen, argon, hydrogen, helium
Space Applications: LOX, LH2, sensor cooling typically below 3 K
Biomedical: cryosurgery, cell preservation)
Other physics applications: Dark matter searches, calorimeters, EXO
Aerospace and military – IR sensing
SRF Systems
While this tutorial will only cover one of these applications, the basic principles taught apply to all of them

Some Examples

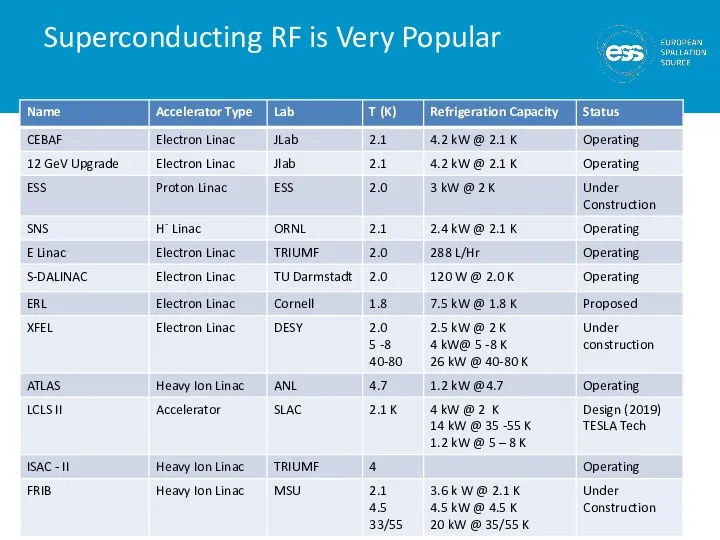
Superconducting RF is Very Popular

Catching Cold
Before we get involved in thermodynamic cycles, let’s go over the basics
There are really only a few ways in which to make a pure fluid such as helium colder
Cause the fluid to do work by making it expand against a piston or turbine while keeping it thermally isolated from the outside environment Isentropic Expansion
Transfer heat from the fluid to a colder surface
Cause the fluid to do “internal work” by expanding it through a valve while keeping it thermally isolated Isenthalpic Expansion
Joule-Thomson expansion (more later)
Once the fluid is a liquid, reduce the pressure above the fluid below atmospheric pressure thus reducing the saturation temperature
All modern cryogenic plants do the first 3. Ones that provide cooling below 4.2 K also do the last item

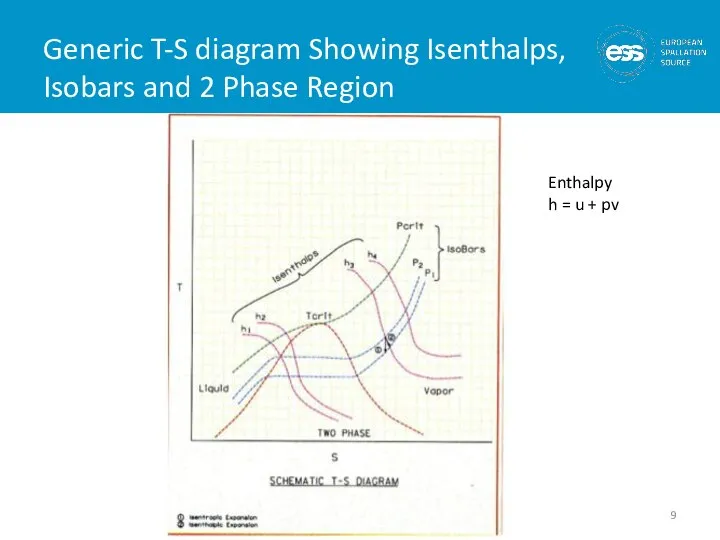
Generic T-S diagram Showing Isenthalps, Isobars and 2 Phase Region
Enthalpy
h = u + pv

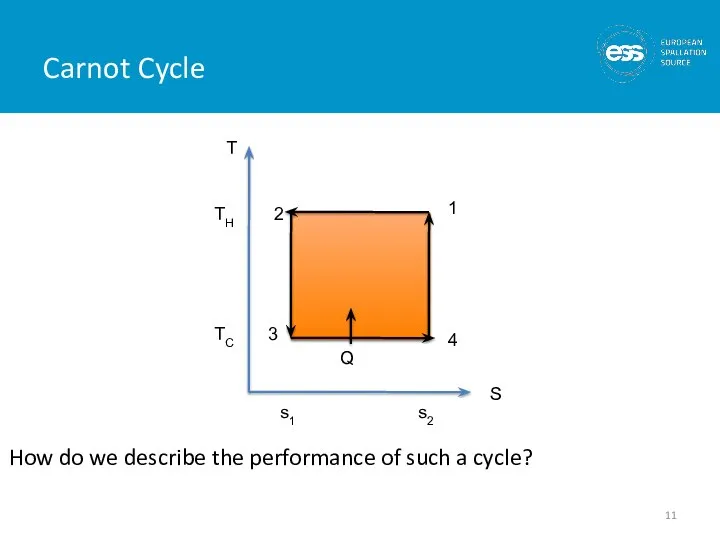
Carnot Cycle
This is an ideal cycle: all processes are reversible
Entropy is only changed by absorbing or removing heat at constant temperature
2nd law of Thermodynamics, in a reversible process dQ = -TdS
The Carnot Consists of 4 steps
Compress the working fluid isothermally at TH (1-2)
Expand the working fluid isentropically from TH to TC (2-3)
Absorb heat into the working fluid isothermally and reversibly at TC (3-4)
Compress the working fluid isentropically from TC to TH (4-1)
Note isentropically = reversibly and adiabatically

Carnot Cycle
How do we describe the performance of such a cycle?

Coefficient of Performance
& the Carnot Cycle
Coefficient of Performance: the heat absorbed from the cold sink divided by the net work required to remove this heat
Minus sign takes into account that the heat absorbed by the cycle is positive while the work done is negative
For the ideal (and in practice unachievable) Carnot cycle it can be shown that:

Coefficient of Performance
& the Carnot Cycle
For a plant operating between room 300 K and 4.2 K, the Carnot COP is
4.2/( 300 – 4.2) or 0.0142
The Carnot cycle is the ideal case. It is the best you can do without violating the laws of thermodynamics
Note that the form of the Carnot COP shows that you have a better COP (thus a more efficient process or refrigerator) if TC is large
It is always thermodynamically more efficient to intercept heat (provide cooling) at higher temperatures
This fact drives a lot of cryogenic design
In practice, we generally discuss the inverse of the COP because this allows us to describe the number of watts of work required to provide 1 Watt of cooling at a given temperature. For a Carnot cycle providing cooling at 4.2 K. This is 70 W/W
People will frequently and incorrectly refer to this as a COP as well

Carnot Cycles & the Real World
Can we build a real machine using a Carnot cycle? In a word NO
Why?
Compressing a fluid isothermally is very hard to achieve, Normally the fluid is compressed and then cooled back down to 300 K
Expanding or compressing fluid isentropically is basically impossible
We can absorb heat into a boiling fluid isothermally but not with out irreversible losses
How close can we get to Carnot? We define the Figure of Merit (FOM) as:
We also speak in terms of “percent Carnot” i.e. FOM of 0.2 is 20% Carnot

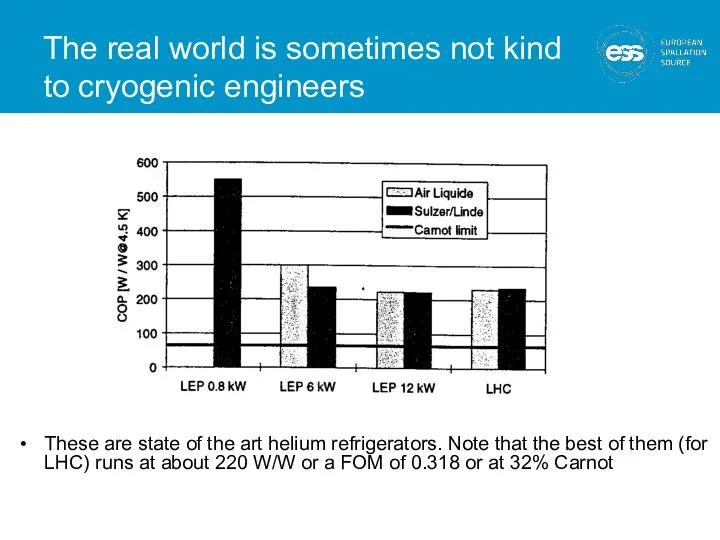
The real world is sometimes not kind to cryogenic engineers
These are state of the art helium refrigerators. Note that the best of them (for LHC) runs at about 220 W/W or a FOM of 0.318 or at 32% Carnot

Practical Impact of Plant Performance
How much power does it take to operate a large cryogenic refrigeration plant?
AT ESS we expect to have a refrigeration plant capable of removing as much as 9.5 kW at 4.5 K. The FOM of the plant is expected to be 0.26
If the plant operates as expected this means we will need:
(66/0.26) x 9500 = 2.4 MW of mechanical power
We are adding some additional margin to the electrical power requirements and have asked for at least 2.6 MW available for powering the compressors

Joule-Thomson Expansion
Isenthalpic (h=constant) expansion
Fluid cools as is it is expanded at constant enthalpy through a valve
However, depending on both the fluid and the temperature, such an expansion can also cause heating.
Define the Joule-Thomson expansion coefficient
μj must be positive for cooling to occur
Cooling by JT expansion has some advantages
No moving parts
Can easily handle two-phase mixtures

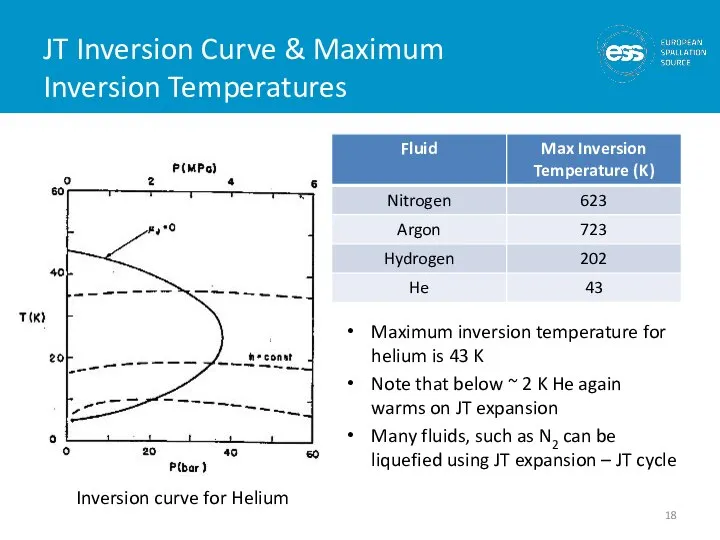
JT Inversion Curve & Maximum
Inversion Temperatures
Maximum inversion temperature for helium is 43 K
Note that below ~ 2 K He again warms on JT expansion
Many fluids, such as N2 can be liquefied using JT expansion – JT cycle
Inversion curve for Helium

Practical Large Scale Helium Refrigerators
Modern large scale Helium refrigerators/liquefiers use a variation of the Claude cycle known as the Collins cycle
The key difference between these cycles and the JT cycle is the addition of expansion engines (pistons or turbines) that the fluid does work against and thus cools
The process through these expansion engines may be idealized as Isentropic (s = constant) expansion
Cooling occurs at any temperature
ΔT for a given ΔP is much larger than for isenthalpic expansion
Claude cycle = 1 expansion engine, Collins cycle = multiple expansion engines
The post WW II development of the Collins liquefier revolutionized laboratory research in cryogenics

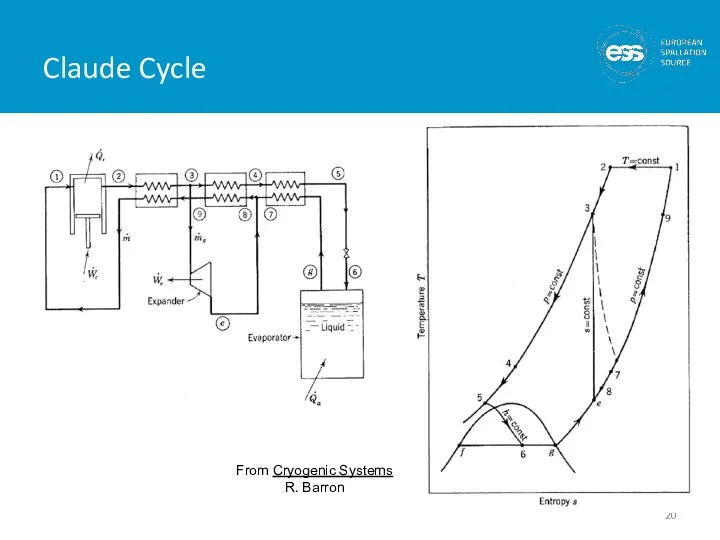
Claude Cycle
From Cryogenic Systems
R. Barron

Cycle consists of :
1) Compression to ~ 16 Bar with cooling back to 300 K + oil removal
2) Cooling of high pressure gas with LN2
3) Isentropic expansion via 2 or more expansion engines
4) Cooling of high pressure gas by the cold returning low pressure stream
5) Isenthalpic expansion through JT valve
6) Return of gas to compressors at just above 1 Bar
Collins Cycle

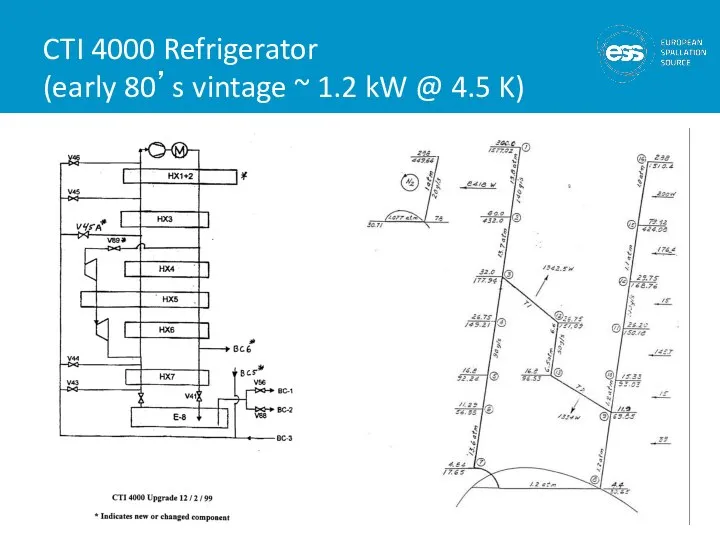
CTI 4000 Refrigerator
(early 80’s vintage ~ 1.2 kW @ 4.5 K)

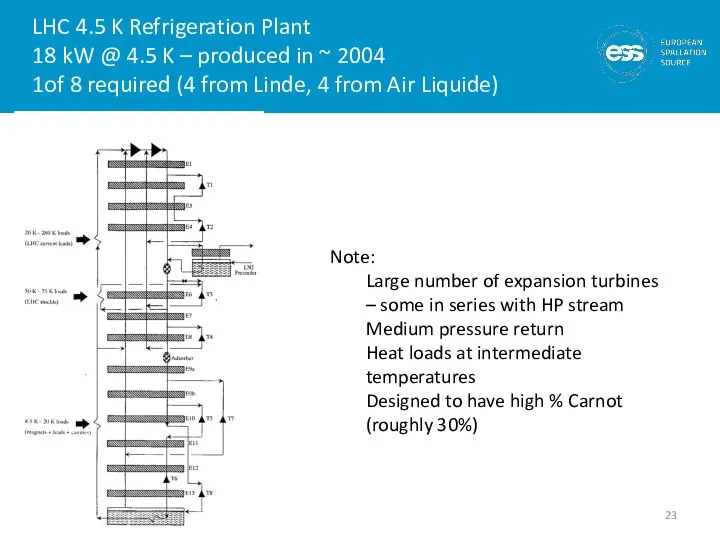
LHC 4.5 K Refrigeration Plant
18 kW @ 4.5 K – produced in ~ 2004
1of 8 required (4 from Linde, 4 from Air Liquide)
Note:
Large number of expansion turbines – some in series with HP stream
Medium pressure return
Heat loads at intermediate temperatures
Designed to have high % Carnot
(roughly 30%)

Refrigerators vs. Liquefiers
Refrigerators are closed cycle systems
They provide cooling and can create liquids but all the mass flow is returned to the start of the cycle
Such systems are said to have “balanced flow”
Liquefiers are open cycle systems
They provide a liquid which is then drawn off and used elsewhere
These have “unbalanced flows” the amount of mass returned to the start of the cycle is less than the amount that started by the mass that was converted to liquid.
In order to keep the cycle running this mass would have to be added as room temperature gas.

Refrigerators vs. Liquefiers
In practice, this distinction is less clear cut
Modern cryogenic plants can operate either as refrigerators or liquefiers and in fact, generally operate as a mixture of the two.
We talk about refrigeration loads & liquefaction loads
A key issue is at what temperature is the boil off gas from a cryogenic liquid returned to the cycle?
If brought back at a cryogenic temperature and used to cool incoming warmer gas then this is a refrigeration load
If brought back warm and not used to cool incoming warmer gas this is a liquefaction load
The thermodynamic rules are the same for refrigerators and liquefiers

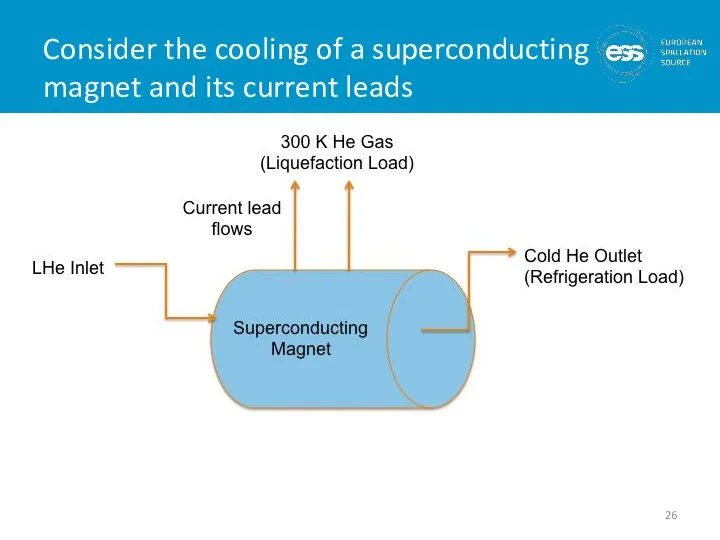
Consider the cooling of a superconducting magnet and its current leads

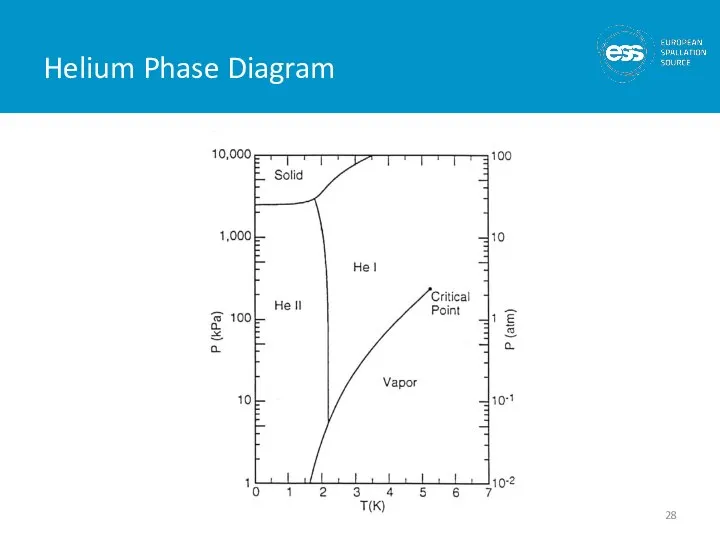
He II (Superfluid Helium)
2nd liquid phase of helium (hence He II)
Phase transition is 2nd order (no latent heat) but there is a discontinuity in the specific heat (λ transition)
Tλmax = 2.2 K
Has unique thermal and fluid properties
High effective thermal conductivity
Zero viscosity under certain conditions

Helium Phase Diagram

Why Use He II in SRF Systems?
The biggest single advantage is the lower temperature (<4.2 K)
Lower temperature means lower BCS losses in cavities, size of effect is RF frequency dependent
He II refrigeration is more costly (due to Carnot & machine inefficiencies)
Generally speaking, removing 1 W at 2 K is the equivalent of removing 3 W at 4.2 K
There is a point at which the gain from lower BCS losses is better than the additional cost of refrigeration
An additional advantage is the very efficient heat transfer mechanism in He II
This results in no bulk boiling which reduces microphonics
The majority of new SRF systems operate in the He II regime

What is He II ?
A “Bose – Einstein like” Condensate
A fraction of atoms in He II have condensed to the quantum ground state
He II was the first of these condensates discovered
The only one that has significant industrial applications
The properties of He II can be understood via the two fluid model

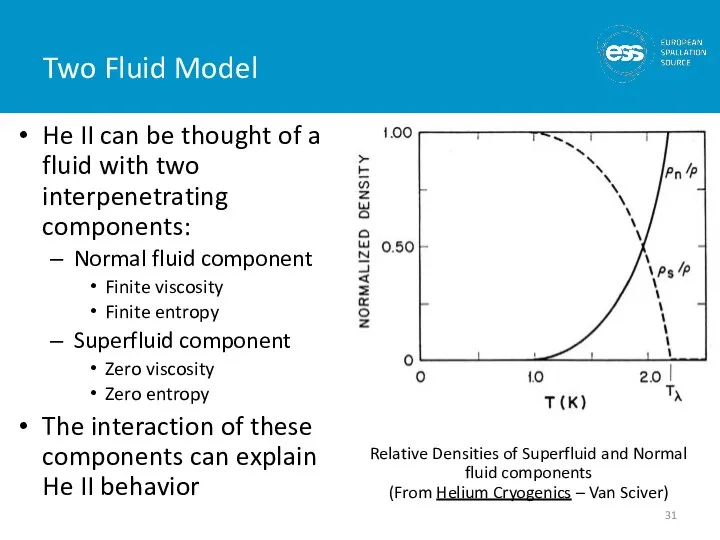
Two Fluid Model
He II can be thought of a fluid with two interpenetrating components:
Normal fluid component
Finite viscosity
Finite entropy
Superfluid component
Zero viscosity
Zero entropy
The interaction of these components can explain He II behavior
Relative Densities of Superfluid and Normal fluid components
(From Helium Cryogenics – Van Sciver)

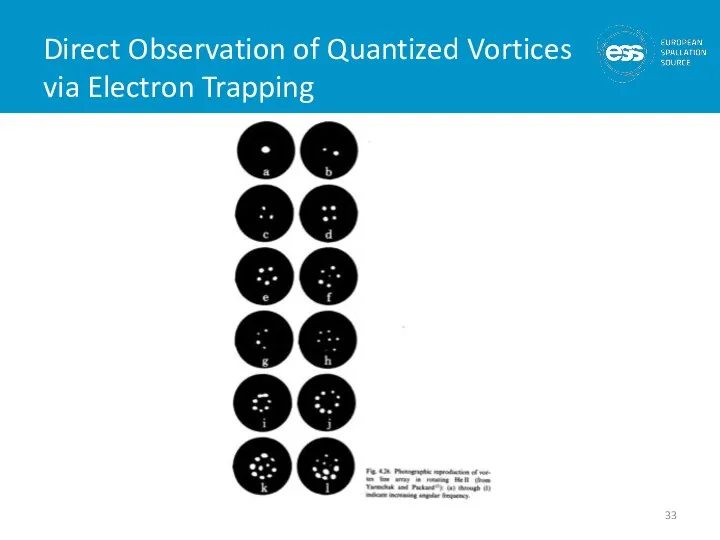
Quantized Vortices
(or does He II at 1 K rotate in a bucket)
At 1 K He II is almost entirely the superfluid component and thus has almost 0 viscosity. This would imply that He at 1 K in a spinning bucket wouldn’t rotate but it does. What’s the answer?
The vortices are quantized:
Solves rotating bucket problem
In the body of the fluid:
At the wall:
This has been experimentally observed
The quantized vortices in the superfluid component are an important part of heat transfer mechanism in He II

Direct Observation of Quantized Vortices via Electron Trapping

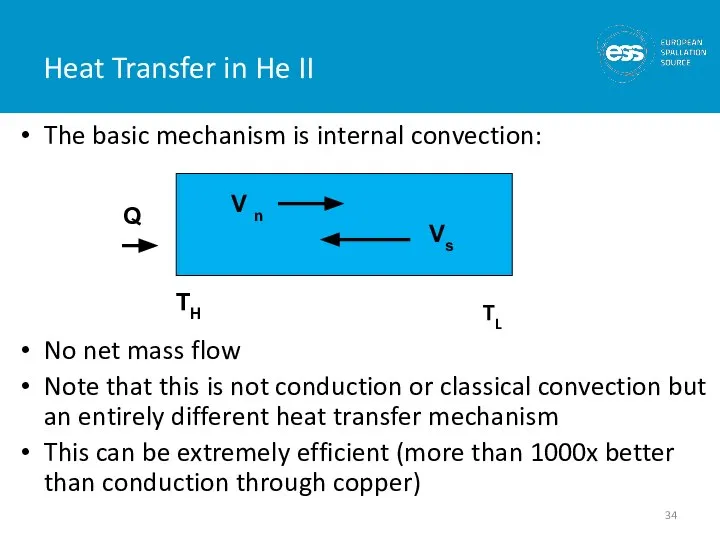
Heat Transfer in He II
The basic mechanism is internal convection:
No net mass flow
Note that this is not conduction or classical convection but an entirely different heat transfer mechanism
This can be extremely efficient (more than 1000x better than conduction through copper)

Heat Transfer in He II
There are 2 heat transfer regimes:
Vs < V sc
Vs > V sc
Mutual Friction Regime (quantized vortices interact with the viscosity of the normal component
As V sc ~ d-1/4 (cgs units) the mutual friction regime is most applicable in engineering applications of He II

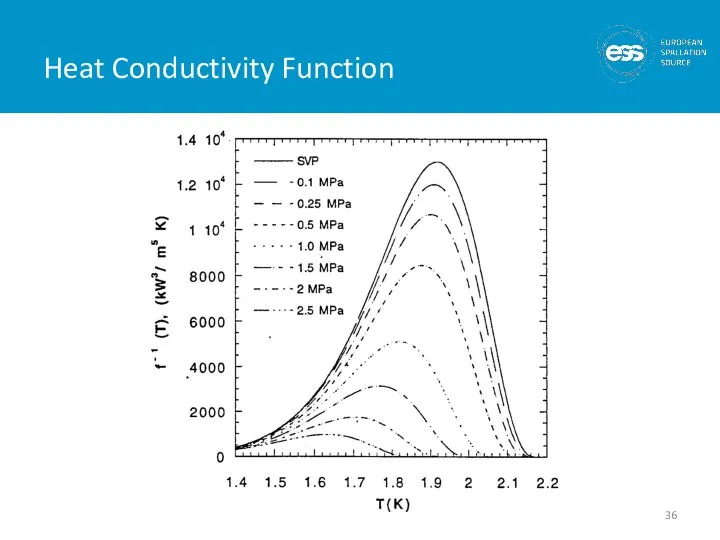
Heat Conductivity Function

He II Heat Transfer Limits
In pressurized He II: T h must be less than T λ
Thus the peak heat flux q* is:
At 1.9 K and 1 bar :
q*L1/3 ~ 15 kW/m5/3

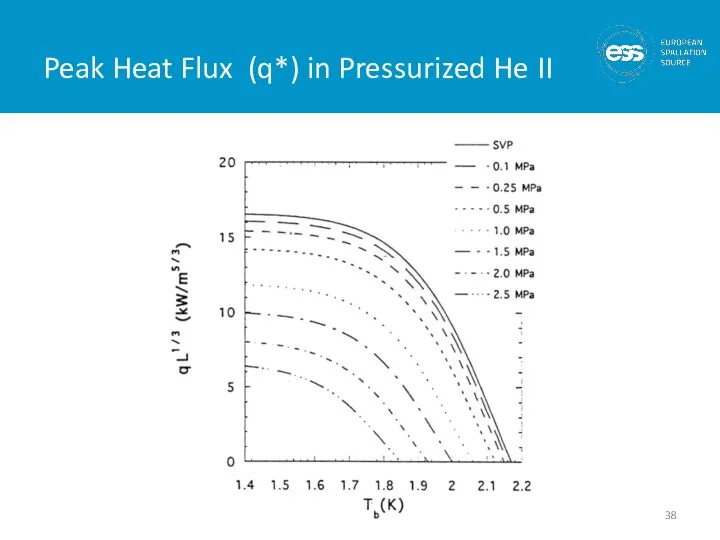
Peak Heat Flux (q*) in Pressurized He II

Limits on He II
Heat Transfer
In saturated He II, the limit is given by the local saturation temperature & the degree of local subcooling
In the ILC cavity He vessel this works out to about 1 W/cm2 or ~ 30 W total through the connection tube
More heat than that would require a redesign
Exceeding the heat transfer limits in either the saturated or pressurized case results in conversion to He I and boiling at the heated surface

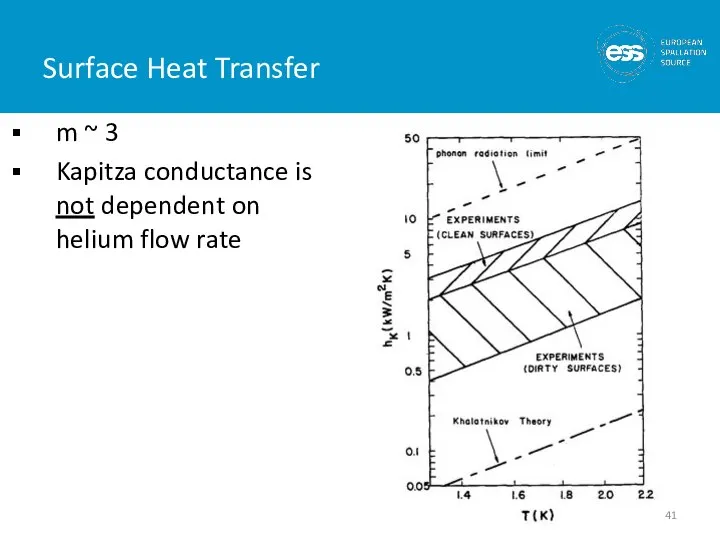
Surface Heat Transfer
Heat transfer from a surface into He II is completely dominated by a fundamental inefficiency in moving energy from the surface to the fluid
This effect exists but is not important in standard convection problems
Normally we assume Tw = Tfw but this is not true in the case of He II
This surface heat transfer effect is described by Kapitza Conductance
For q < 1 kW/m2
For q > 1 kW/m2
h k, a and m are empirical and dependent on material, temperature and surface condition

Surface Heat Transfer
m ~ 3
Kapitza conductance is not dependent on helium flow rate

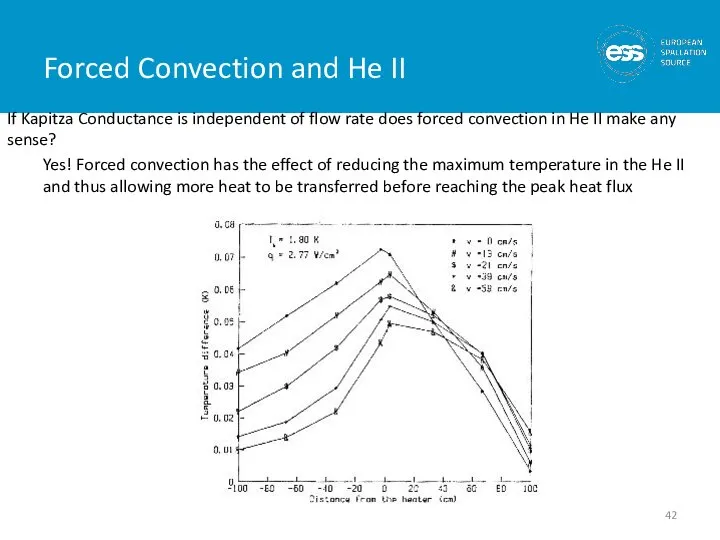
Forced Convection and He II
If Kapitza Conductance is independent of flow rate does forced convection in He II make any sense?
Yes! Forced convection has the effect of reducing the maximum temperature in the He II and thus allowing more heat to be transferred before reaching the peak heat flux

He II Fluid Dynamics
Despite the presence of the superfluid component, in almost all engineering applications He II behaves as a classical fluid. This includes :
Pump performance
Except cavitation in saturated He II
Pressure drop in tubes, valves, bellows and fittings
Flow metering techniques
This is likely a result of the quantized vortices in the superfluid component being coupled via mutual friction to the normal fluid viscosity
However, keep in mind that the unique heat transfer properties still exist as described.

He II Fluid Dynamics
He II does behave differently in cases of:
Film flow
Porous plugs
Two – phase flow (liquid/vapor) due to the large density difference between liquid and vapor in the case of He II

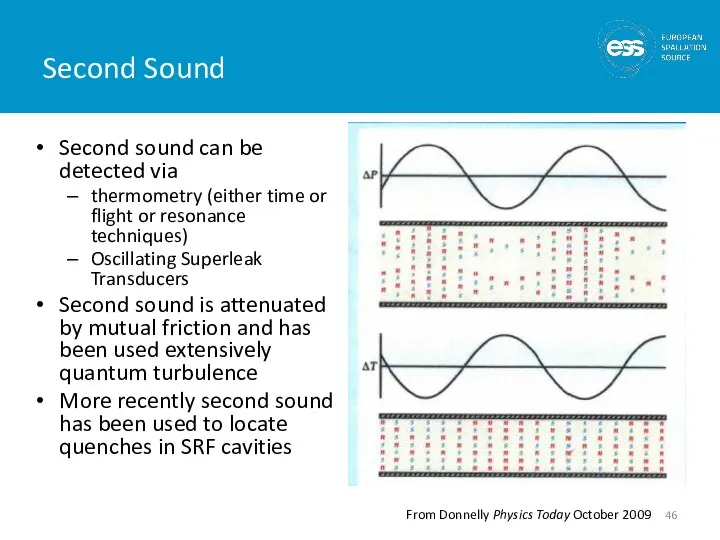
Second Sound
The two-fluid model predicts and experiments show that temperature waves may be established in the He II due to oscillations in the local entropy. These temperature waves are known as second sound as they are analogous to density waves caused by pressure oscillations.
Recall that the superfluid component has zero entropy
From Helium Cryogenics S.W. Van Sciver (2013)

Second Sound
Second sound can be detected via
thermometry (either time or flight or resonance techniques)
Oscillating Superleak Transducers
Second sound is attenuated by mutual friction and has been used extensively quantum turbulence
More recently second sound has been used to locate quenches in SRF cavities
From Donnelly Physics Today October 2009

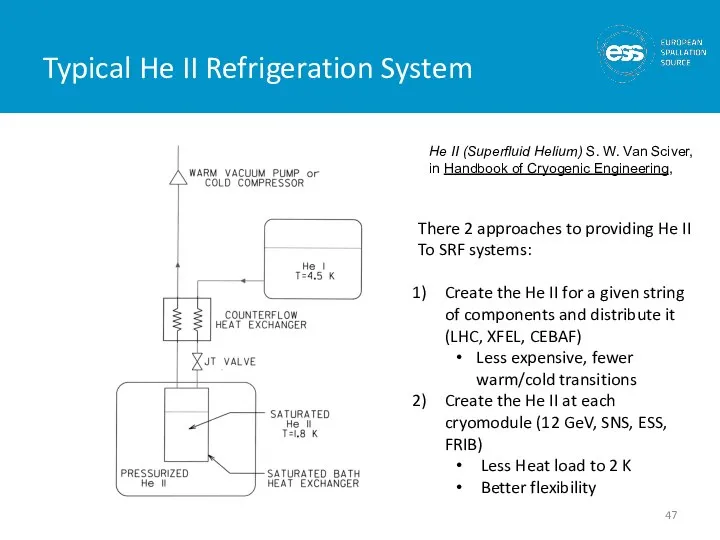
Typical He II Refrigeration System
He II (Superfluid Helium) S. W. Van Sciver, in Handbook of Cryogenic Engineering,
There 2 approaches to providing He II To SRF systems:
Create the He II for a given string of components and distribute it (LHC, XFEL, CEBAF)
Less expensive, fewer warm/cold transitions
Create the He II at each cryomodule (12 GeV, SNS, ESS, FRIB)
Less Heat load to 2 K
Better flexibility