Слайд 3Постановка задачи
Если входные и выходные переменные модели непрерывные — перед нами задача

регрессии.
Если выходная переменная одна и она является дискретной (метка класса), то речь идет о задаче классификации.
Слайд 4Этап первый
Поскольку метка класса каждого примера предварительно задана, построение классификационной модели часто

называют обучением с учителем.
В процессе обучения формируются правила, по которым производится отнесение объекта к одному из классов
Слайд 5Этап второй
модель применяется для классификации новых, ранее неизвестных объектов и наблюдений

Слайд 6Линейная регрессия
Задача линейной регрессии заключается в нахождении коэффициентов уравнения линейной регрессии, которое

имеет вид:
y = b0 + b1 x1 + b2 x2 + ...+ bn xn ,
где y — выходная (зависимая) переменная модели;
x1, x2,…, xn — входные (независимые) переменные;
bi — коэффициенты линейной регрессии (b0 — свободный член).
Слайд 7Задача линейной регрессии заключается в подборе коэффициентов bi уравнения таким образом, чтобы

на заданный входной вектор X = (x1, x2,…, xn)T регрессионная модель формировала желаемое выходное значение y
Слайд 9Линия регрессии — это прямая наилучшего приближения для набора пар значений входной
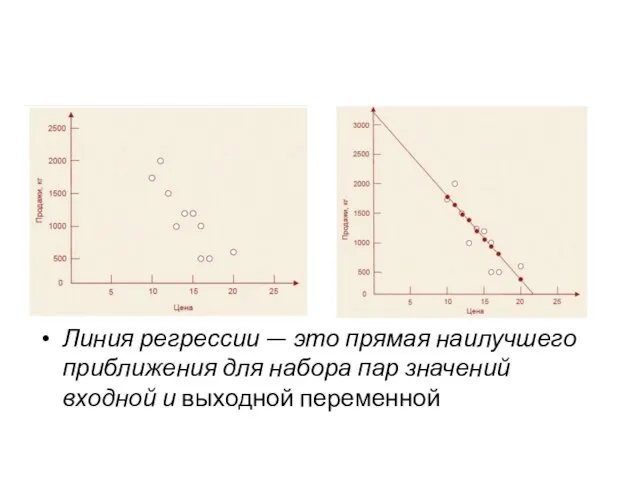
и выходной переменной
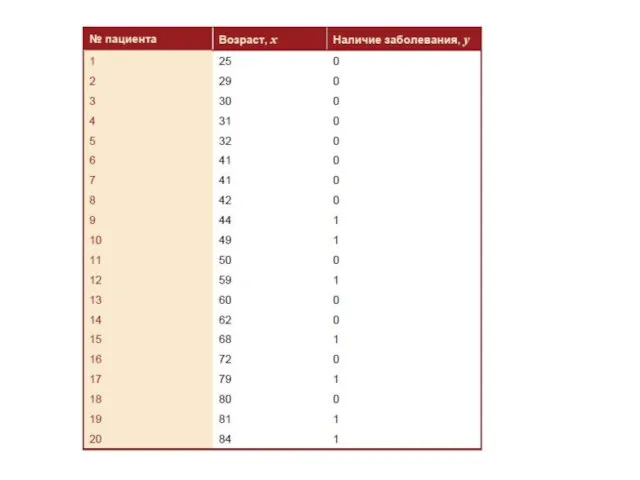
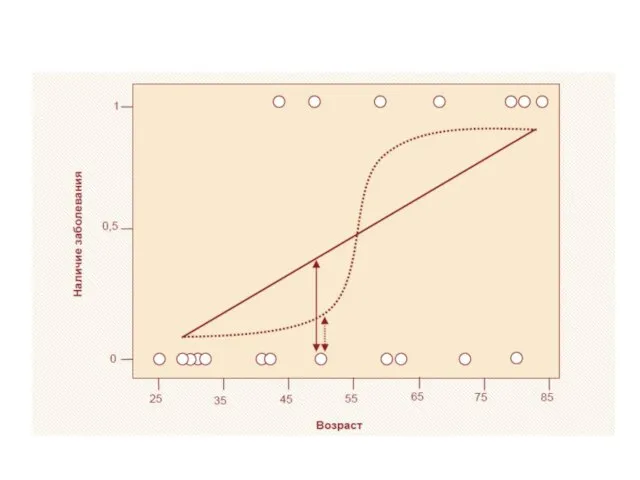
Слайд 10Логистическая регрессия
задачи предсказания вероятности некоторого события в зависимости от значений набора независимых

переменных
логистическая регрессия служит не для предсказания значений зависимой переменной, а для оценки вероятности того, что зависимая переменная примет заданное значение.
Слайд 13Деревья решений
Методы, основанные на обучении

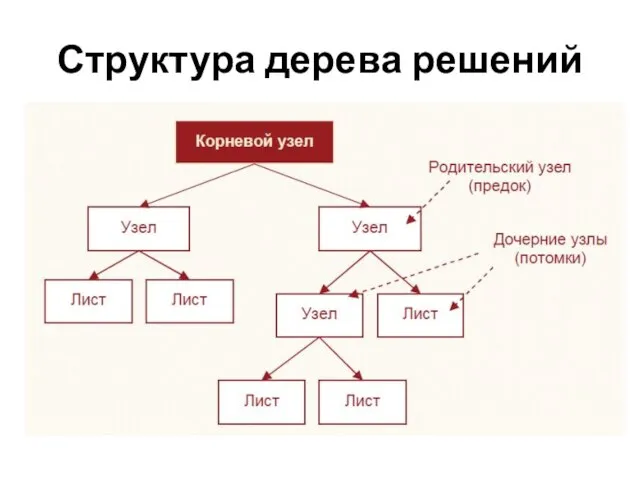
Слайд 14 Дерево решений — это древовидная иерархическая модель, где в каждом узле

производится проверка определенного атрибута (признака) с помощью правила
Деревья решений — иерархические древовидные структуры, состоящие из решающих правил вида «если… то…» и позволяющие выполнять классификацию объектов. В дереве каждому объекту соответствует единственный узел, дающий решение.
Слайд 15Деревья решений — это модели, основанные на обучении. Процесс обучения сравнительно прост

в настройке и управлении.
Процесс обучения деревьев решений быстр и эффективен.
Деревья решений универсальны — способны решать задачи как классификации, так и регрессии.
Деревья решений обладают высокой объясняющей способностью и интерпретируемостью.
Слайд 16Построение дерева
Описание атрибутов
Предварительное определение классов
Различимость классов
Полнота данных

Слайд 18Принцип «разделяй и властвуй»
2 3
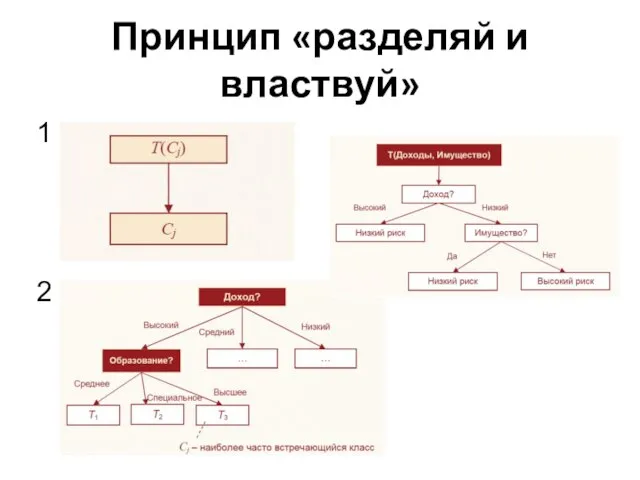
Слайд 19Искусственные нейронные сети
Методы, основанные на обучении

Слайд 20Искусственная нейронная сеть представляет собой параллельно-распределенную систему процессорных элементов (нейронов), способных выполнять
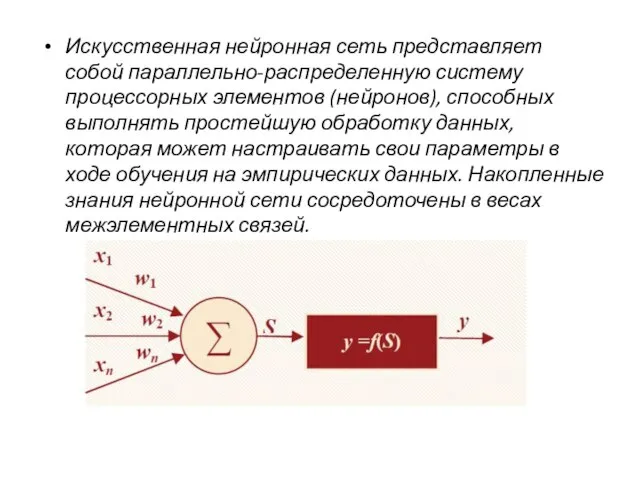
простейшую обработку данных, которая может настраивать свои параметры в ходе обучения на эмпирических данных. Накопленные знания нейронной сети сосредоточены в весах межэлементных связей.
Слайд 21свойства нейронных сетей
Нелинейность.
Обучение на примерах
Параллельная обработка данных.
Адаптивность.
Отказоустойчивость.

Слайд 22Входные данные хорошо интерпретируются
Желаемые результаты также хорошо интерпретируются
Доступный опыт

Слайд 23Выбор числа нейронов в многослойном персептроне
Число нейронов во входном и выходном слоях

жестко определяется числом входных и выходных переменных модели соответственно.
Число нейронов в скрытых слоях и число скрытых слоев выбираются таким образом, чтобы количество образованных ими связей было как минимум в два-три раза меньше числа обучающих примеров.


















 Родительское собрание Первый раз в первый класс
Родительское собрание Первый раз в первый класс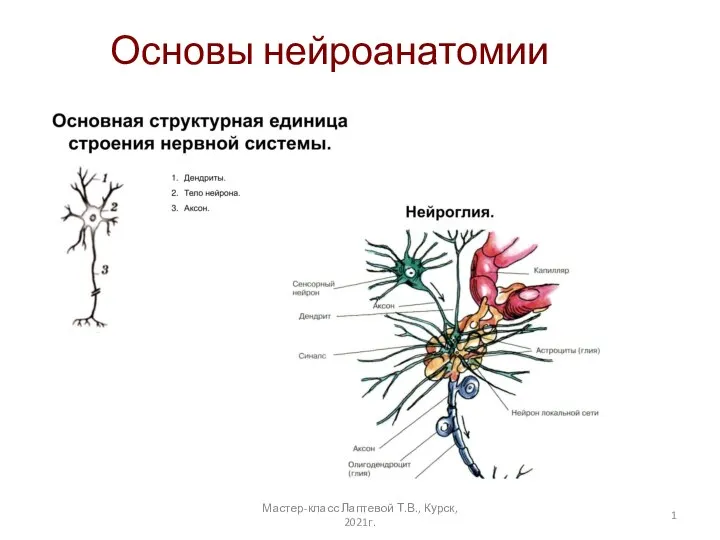 Основы нейроанатомии
Основы нейроанатомии Политическая система общества
Политическая система общества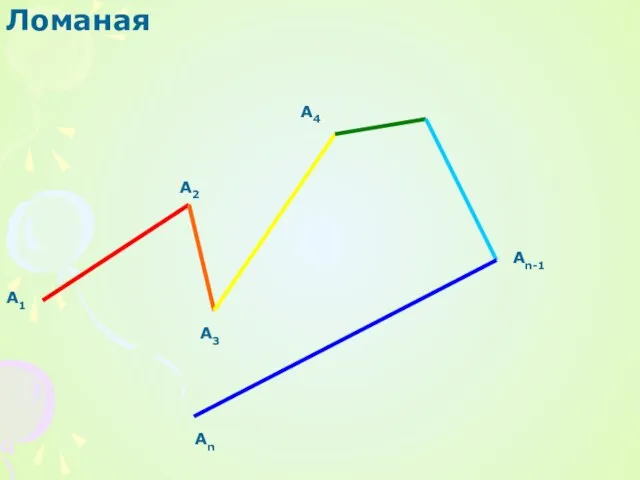 Презентация на тему Ломаная
Презентация на тему Ломаная Интеллектуальное оповещение дежурно-диспетчерского персонала ДЦС-7
Интеллектуальное оповещение дежурно-диспетчерского персонала ДЦС-7 Презентация на тему Боги Древних Славян
Презентация на тему Боги Древних Славян Нефтяная и газовая промышленность Украины
Нефтяная и газовая промышленность Украины Влияние алкогольных напитков на жизнь человека
Влияние алкогольных напитков на жизнь человека Организация конкурса на заключение договора о целевом обучении
Организация конкурса на заключение договора о целевом обучении Курс «Управление рисками и страхование»
Курс «Управление рисками и страхование» Местоимение. Pronom personnel “y”
Местоимение. Pronom personnel “y” Випуск 1992 року
Випуск 1992 року Презентация на тему My Working Day
Презентация на тему My Working Day Ядовитость спиртов
Ядовитость спиртов Свойства альдегидов, их применение.
Свойства альдегидов, их применение. Профессиональные сообщества как инструмент управления знаниями
Профессиональные сообщества как инструмент управления знаниями ИЗМЕРЕНИЕ ИНФОРМАЦИИ ИНФОРМАЦИЯ И ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ
ИЗМЕРЕНИЕ ИНФОРМАЦИИ ИНФОРМАЦИЯ И ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ  Проект Чистый газон (Не дай краснеть своей собаке)
Проект Чистый газон (Не дай краснеть своей собаке) Для любителей математики и не только…
Для любителей математики и не только… students work Case 4
students work Case 4 Тундра (4 класс)
Тундра (4 класс) Приготовление песочного теста
Приготовление песочного теста Сестринский процесс при болезнях почек
Сестринский процесс при болезнях почек Вольфганг Амадей Моцарт
Вольфганг Амадей Моцарт Конфлікти в закладі дошкільної освіти
Конфлікти в закладі дошкільної освіти Движение по окружности
Движение по окружности Власть как политический феномен. Политическая система общества. Государство
Власть как политический феномен. Политическая система общества. Государство | Ключ к неорганическим материалам
| Ключ к неорганическим материалам